Optimization Problems
비용의 측면에서는 최소, 이익의 측면에서는 최대가 되어야 한다. 가능한 모든 결과에 대해 분석하고 최적의 해가 되도록 선택을 해주면 된다.
Greedy Algorithms
그 당시의 최선의 선택이었다고 하더라도 나중에 번복하면 안된다. 지금이 예전보다 더 좋은 방법이 생겨도 이미 과거에 선택을 했다면 돌이킬 수 없다.
Minimum Spanning Tree
Spanning tree
Spanning tree는 undirected tree이다. 즉, G의 버텍스는 모두 포함하여야만 하고 connected, acyclic, undirected 특성을 모두 지녀야만 한다.
Minimum Spanning Tree는 특정 값의 크기를 비교할 수 있어야만 하므로 가중 트리(weighted tree)여야만 한다. 한마디로 spanning tree속성에 weighted 속성이 추가적으로 포함되어야 한다.
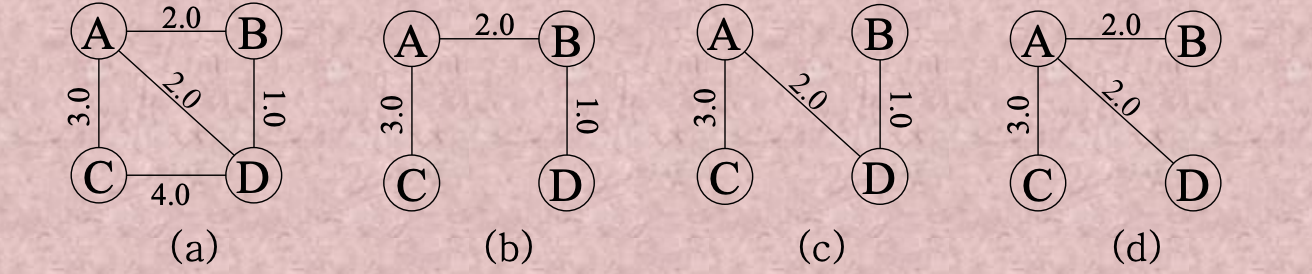
(a)가 그래프 G이고 (b), (c), (d)가 spanning tree subgraph이다. Minimum Spanning Tree는 subgraph의 weight 합이 최소가 되는 트리를 말하는데 여기서는 (b), (c)가 Minimum Spanning Tree이다. 반드시 하나가 아닐 수도 있다.
Prim's Algorithm
시작 버텍스를 임의로 선택해준다. 그 시작 버텍스는 루트의 역할을 한다. 그리고 루프를 통해 확장해줄 것이다. 시작 버텍스에서 확장할 때 greedy algorithm을 이용하여 weight가 작은 값을 선택한다. 버텍스를 Minimum Spanning Tree에 추가해줄 때 중복되는 값을 추가하지 않기 위해서 상태를 표시해주는데 이 상태의 종류는 다음과 같다. 이 중에서 하나는 만족해야 한다.
- Tree vertices: 이미
Minimum Spanning Tree에 포함된 버텍스를 의미한다. - Fringe vertices:
Minimum Spanning Tree에는 없지만 후보(인접한)인 버텍스를 의미한다. - Unseen vertices: 아직 살펴보지 않은 버텍스를 의미한다.

우선 사전 순으로 A부터 살펴보기로 하자. A의 인접한 노드는 unseen 단계에서 Fringe 단계로 업데이트가 된다. 그리고 weight를 비교해서 작은 것을 선택해 해당 Fringe를 Tree로 업데이트 해주고 또 인접한 노드는 Fringe로 업데이트 해준다.
그렇다면 가중치에 대한 정보는 어떻게 입력할 수 있을까? 이것에 대해서는 min-priority queue를 이용하면 된다.
| - | Unsorted sequence | Soted sequence | heap |
|---|---|---|---|
| insert() | O(1) | O(n) | O(log N) |
| removeMin() | O(n) | O(1) | O(log N) |
| decreaseKey() | O(1) | O(n) | O(log N) |
보통은 sorted sequence와 같은 경우는 수행시간이 길어서 나머지 두개 중 하나를 상황에 맞게 사용하고는 한다.
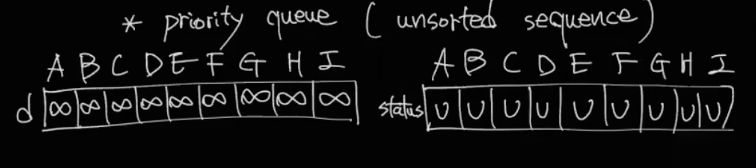
위 그림은 unsorted sequece를 이용하여 프림 알고리즘을 수행한 것이다. 우선 weight를 담은 배열 하나와, 상태를 표현할 수 있는 배열 하나를 생성한다. 전자 배열의 값은 모두 무한대로 초기화하고 후자 배열의 값은 U로 초기화 한다. A지점에서 시작하므로 A는 0과 T로 업데이트 한다. 그리고 A와 인접한 노드의 상태를 F로 바꾸고 weight도 바꾼다.

계속 진행을 하는데 주의해야할 점은 새로운 Tree의 Finge로 업데이트할 때 기존의 weight보다 작은 값이라면 배열도 그에 맞게 업데이트 해줘야 한다.
Unsorted sequence를 이용했을 때 수행 시간은 O(n^2) time이다.
Heap을 이용했을 때 수행 시간은 O(m log N) time이다.
Kruskal's Algorithms
모든 엣지의 집합을 R에 카피할 것이다. R에서 반복문을 통해서 엣지를 하나하나 처리할 것이다. F가 n-1개의 엣지가 되었다면 F를 리턴한다. 이 알고리즘의 가장 핵심은 find(u) 함수와 union(u,v) 함수인데 전자는 버텍스 u를 포함하는 리더를 리턴하고, 후자는 두 버텍스가 서로 다른 set(다른 리더)이면 하나로 합쳐준다. 여기서 크기가 작은 집합이 큰 집합으로 흡수된다.
우선 모든 엣지에 대한 정보가 R에 카피가 되어있다. 그리고 weight가 가장 작은 값을 찾는다. 그리고 연결된 버텍스가 다른 Set이라면 union을 해준다(F에 weight도 추가한다). 그리고 그 다음으로 weight가 작은 값을 찾는다. 또 다르다면 union을 해준다(F에 weight도 추가한다). 이렇게 반복하는데 만약 같은 집합이 나오면 그냥 스킵한다. 이렇게 F가 n-1이 되면 그때가 minimal spanning tree가 된다.
수행 시간 : O(m log m) time인데 O(m log n) time으로 해도 가능하다. m은 O(n^2)에 수렴하는데 뒤에 m을 n^2으로 바꾸면 로그의 성질로 인해 2가 무시 가능하여 O(m log N) time이 된다.
Shortest Paths
Single-Source shortest Paths
소스 버텍스로부터 다른 버텍스까지의 최단경로를 측정하는 것을 의미한다. 인풋으로 G와 소스s가 주어진다.
Single-destination shortest paths
인풋으로 G와 목적지인 t가 주어진다. t를 마치 s인 것처럼 수행을 해주고 나중에 방향만 바꿔주면 된다.
Single-pair shortest paths
인풋으로 G와 소스s와 목적지 t가 주어진다.
All-pairs shortest paths
인풋으로 그래프 G만 주어진다.
X부터 Z까지가 Shortest-Paths 이고, 중간에 Y를 거쳐간다면 X부터 Y도 Shortest-Paths 이고, Y부터 Z까지도 Shortest-Paths 이다. 이러한 것을 optimal substructure라고 한다. 하지만 이 역은 성립하지 않는다.
Dijkstra's Shortest-Path Algorithm
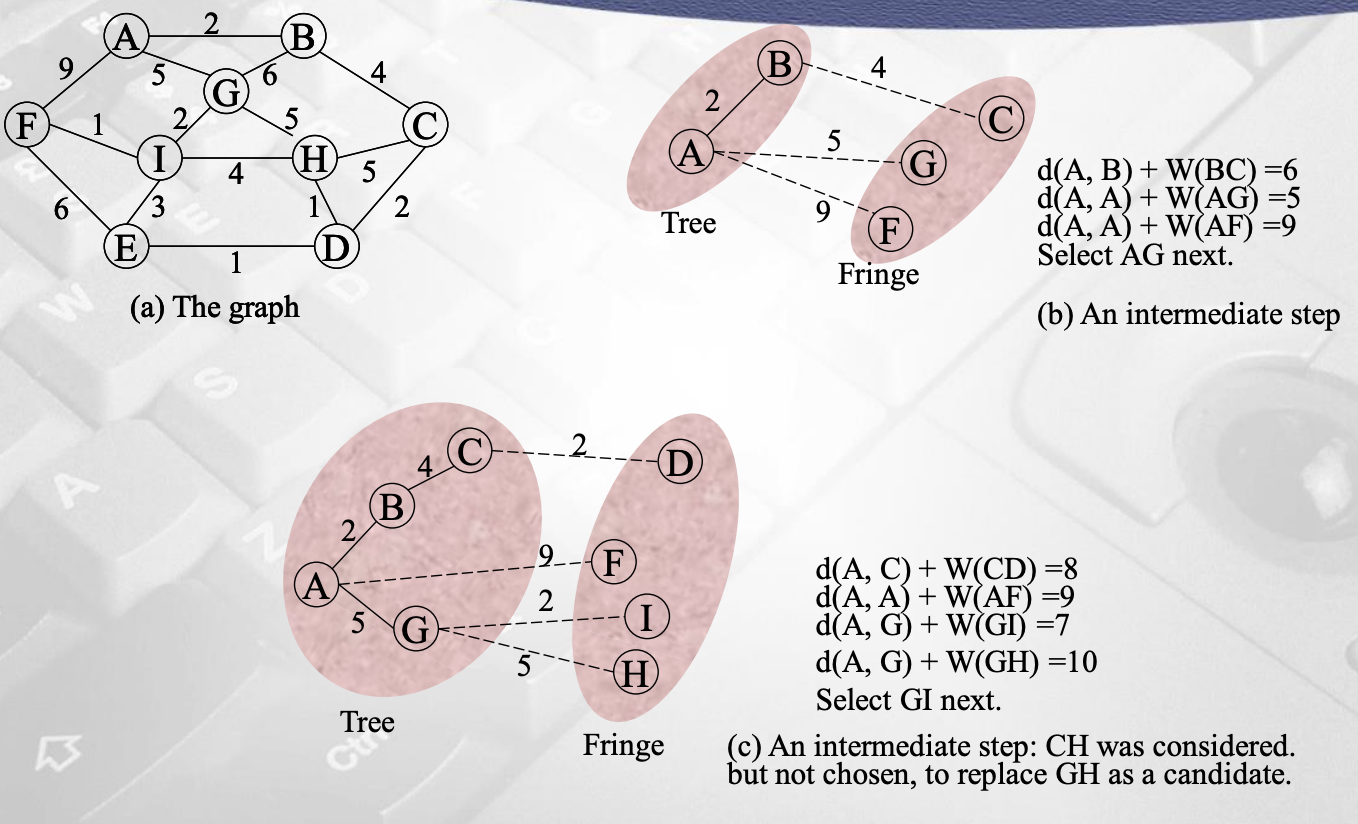
여기서 weight는 무조건 양수이다. 그리고 프림의 알고리즘과 매우 유사하다. 여기서도 버텍스의 상태를 Unsean, tree, fringe로 둘 수 있다. weight가 작은 것을 연결할 때마다 shortest-path tree 는 점점 커진다. 여기서 프림의 알고리즘과 다른 점은 단순히 현재 버텍스로부터 fringe의 weight만 고려하는 것이 아니라 루트로부터 가고자 하는 거리를 고려한다. 기존에 weight값이 있다면 루트로부터 연결되는 새로운 거리가 더 짧다면 교체해준다. 예시로 한번 확인하자.

여기까지가 while문을 수행하기 이전까지의 상태이다.

위 그림을 한번 해보면서 비교해보자.
프림의 알고리즘과 다르게 parent 배열을 만들었기 때문에 기준이 되는 index에서부터 차례대로 스택에 저장한다. -1을 만나기 전까지 저장해서 shortest path를 구하면 된다.
Unsorted sequence를 이용했을 때 수행 시간은 O(n^2) time이다.
Heap을 이용했을 때 수행 시간은 O(m log N) time이다.