머신러닝 - 분류와 군집화

Jae Chan·2023년 5월 7일

군집화 머신러닝 분류

TIL

목록 보기

7/10

지난 글에서 작성한 회귀에 이어서 분류와 군집화에 대해 다뤄보자.

두 가지의 방법 모두 데이터를 비슷한 집단으로 묶는 유사한 점이 있다.

분류 : 소속 집단의 정보를 이미 알고 있는 상태에서 비슷한 집단으로 묶는 방법
군집화 : 소속 집단의 정보가 없는 상태에서 비슷한 집단으로 묶는 방법

`K-NN` 알고리즘

🧠
입력된 데이터와 가장 가까운 k개의 이웃을 찾아서 다수결의 원칙에 따라 분류하는 알고리즘이다. 이 알고리즘은 지도학습의 대표적인 분류 알고리즘 중 하나이다.

➡️ 동작 과정

입력된 데이터와 학습 데이터 간의 거리를 계산한다.
계산 방법으로는 유클리드 거리, 맨하탄 거리등이 있다.
계산된 거리를 기준으로 가장 가까운 k개의 이웃을 선택한다.
다수결 원칙에 따라 분류를 진행하며, 이 때 분류 방법으로는 가장 많은 클래스를 선택하는 대다수 원칙이 사용된다.

✅ 특징

데이터 인스턴스, 클래스, 특징의 요소들의 개수가 많다면, 많은 메모리 공간과 계산 시간이 필요하다는 단점이 있다.
알고리즘이 매우 단순하고 직관적이며, 사전 학습이나 특별한 준비 시간이 필요 없다는 장점이 있다.

분류 문제의 간단한 사례로 우리 주변에서 볼 수 있는 개의 품종 중에는 닥스훈트와 사모예드라는 종이 있다. 두 종은 몸의 높이와 길이 비율이 서로 다르다.

일반적으로 닥스훈트는 몸통 길이에 비해 몸통 높이가 낮다.
사모예드의 경우 몸통 길이와 높이가 비슷한 특징이 있다.

여기서, 몸통의 길이와 높이를 특징이라 보고 각각 𝑥1, 𝑥2 이라 두고 이 개들의 표본 집합에 대하여 𝑥1, 𝑥2를 측정하면 아래 그림의 오른쪽과 같은 산포도 그래프를 얻을 수 있다.

💡 여기서 산포도 그래프의 위쪽에 분포한 파란색 점은 사모예드 종,
아래쪽의 붉은 점들은 닥스훈트 종이다.

여기서 데이터를 효과적으로 분류하기 위해 K-NN 알고리즘을 적용하면 다음과 같다.

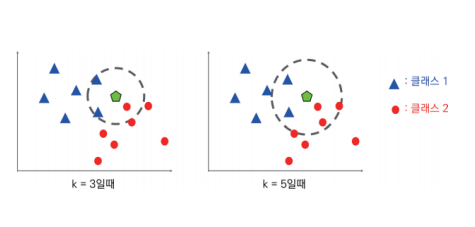
k가 4와 같이 짝수이고 클래스 1과 클래스 2의 개수가 같은 경우에도 새 데이터의 클래스를 판정하는 방법은?

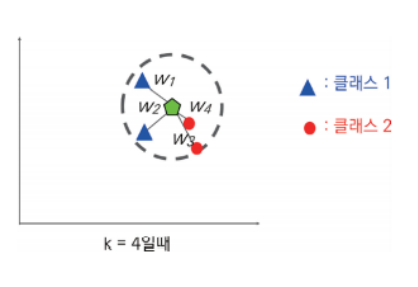
➡️ 2개의 빨간색 원은 다른 2개의 파란색 삼각형보다 더 가까이 있다는 것을 고려해서 클래스 2로 분류한다.

위의 사례를 Python으로 적용해보자.

닥스훈트와 사모예드의 데이터를 예시로 만들고 시각 그래프를 만든다.

import matplotlib.pyplot as plt
import numpy as np

# 닥스훈트의 길이와 높이
dach_length = [77, 78, 85, 83, 73, 77, 84]
dach_height = [25, 26, 29, 29, 23, 24, 30]

# 사모예드의 길이와 높이 데이터
samoyed_length = [81, 82, 83, 86, 79, 83, 84]
samoyed_height = [56, 57, 50, 53, 60, 53, 52]

# 시각 그래프를 그립니다.
plt.scatter(dach_length, dach_height, c='red', label='Dachshund')
plt.scatter(samoyed_length, samoyed_height, c='blue', label='Samoyed')

plt.xlabel('Length')
plt.ylabel('Height')
plt.title("Dogs Size")
plt.legend(loc='upper left')
plt.show()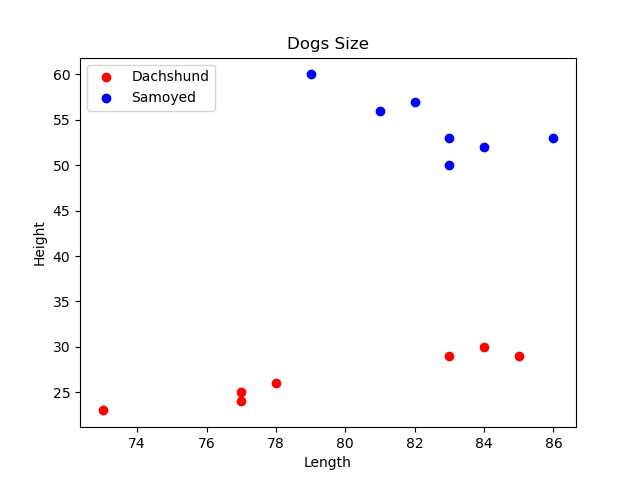

💡 여기서 길이와 높이가 79,35인 새로운 데이터가 들어오고, 이 특징을 가진 개의 종류를 모를 경우 어떤 개로 분류하는 것이 바람직할까?

준비된 데이터에 k-NN 알고리즘을 적용해보겠다.

# 몸통의 길이와 높이 데이터를 묶어 새로운 배열을 만든다.
d_data = np.column_stack((dach_length, dach_height))
d_label = np.zeros(len(d_data))

s_data = np.column_stack((samoyed_length, samoyed_height))
s_label = np.ones(len(s_data))

# 새로운 데이터
newData = [[79, 35]]

# 사모예드 & 닥스훈트 데이터 합치기.
dogs = np.concatenate((d_data, s_data))
labels = np.concatenate((d_label, s_label))

dog_classes = {0: 'Dachshund', 1: 'Samoyed'}

# k 값 = 3 [kNN 분류기]
k = 3
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(dogs, labels)
y_pred = knn.predict(newData)
print("새로운 데이터 : ", newData)
print("판정 결과 : ", dog_classes[y_pred[0]])

결과

새로운 데이터 :  [[79, 35]]
판정 결과 :  Dachshund

k-NN 알고리즘을 통해 실제 데이터를 다룰 경우 99%의 정확도를 가지는 분류기는 매우 구현하기 어려우며, 더구나 단 두 줄 만으로 만든 아래의 분류기는 매우 신뢰하기 힘들다.

# 입력값에 관계없이 Samoyed를 반환한다.
def classfier_A(length, height):
	return 'Samoyed`

표집 편향과 성능 측정을 위한 평가지표

분류기 A가 입력으로 9,900마리의 사모예드와 100 마리의 닥스훈트 종의 길이와 높이를 받는다고 가정한다.

분류기 A의 정확도는 다음과 같다.

분류기 A의 정확도	= 제대로 분류한 데이터 / 전체 데이터
				= 9,900 / 10,000
				= 0.99 (= 99 %)

표본 데이터가 편향된 경우 우수한 머신 러닝 알고리즘을 사용한다고 할지라도 학습 성능의 개선을 기대하기 힘들다.
→ 이를 표집편향(Sampling Bias)이라고 한다.

정밀도(Precision)와 재현율(Recall)을 살펴보고 이 성능을 행렬형태로 표시한
혼동행렬(Confusion Matrix) 혹은 오차행렬에 대해 알아보자.

100명의 환자와 100명의 건강한 사람에 대해 COVID-19 검사 키트의 성능을 테스트 한다고 가정한다.

상황

검사 키트가 COVID-19 환자(양성 Positive : P)에 대해 5명의 음성 결과가 나왔음.
COVID-19에 감염되지 않은 건강한 사람(음성 Negative : N)에 대해서 89명을 음성으로, 11명을 양성으로 판정했다.

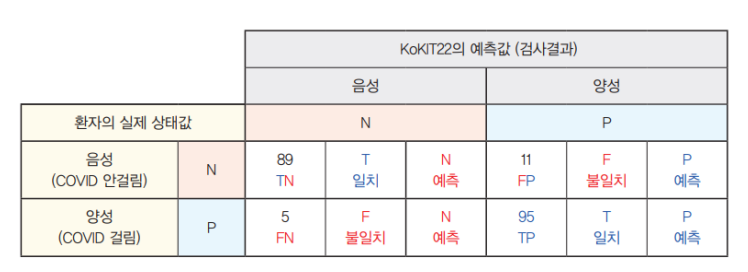
정확도 (Acc)

여기서 정확도는 다음식을 이용해 구한다.

전체 데이터(FP + FN + TP + TN)중에서 제대로 판정한 데이터(TP + TN)의 비율이 바로 이 값이다.

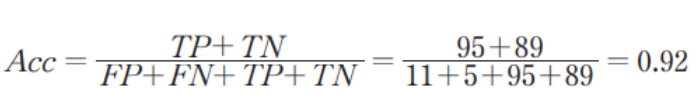
재현율 (Recall)

진짜 양성 비율(True Positive Rate)은 재현율이라고 한다.

COVID-19 양성 환자 중에 이 키트가 올바르게 양성이라고 분류한 환자의 비율로, 다음과 같은 식을 적용한다.

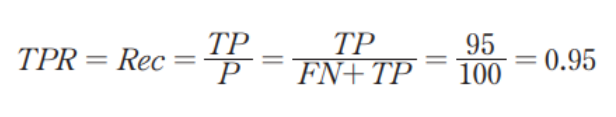
정밀도 (Precision)

정밀도는 검사 키트가 확진자로 분류한 사람들 중에 실제 양성인 경우로 다음과 같은 식을 적용한다.

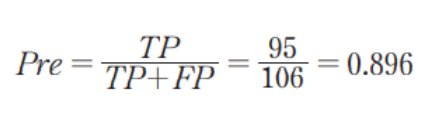
즉 여기서 알 수 있는 점은

재현율 : 실제로 COVID-19의 양성인 대상자를 양성으로 분류할 확률이다.
정밀도 : 양성으로 예측한 사람들 중에서 실제 COVID-19 양성자일 확률이다.

⚠️ 재현율과 정밀도라는 각각의 지표는 관심 척도가 다르기 때문에,
하나의 척도만을 측정 방법으로 사용할 경우에 왜곡이 발생할 수 있다.

두 지표를 조합한 F1 점수도 사용하는 데, 이 점수는 다음과 같은 식이다.
이를 조화 평균(Harmonic Mean)이라고 한다.

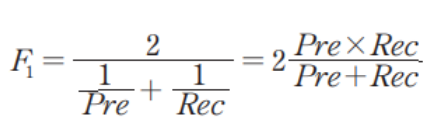
혼동행렬(Confusion Matrix)

혼동행렬은 분류 모델의 성능을 평가하기 위한 행렬이다.
이 행렬은 분류 모델이 예측한 결과와 실제 결과를 비교하여 분류 결과의 정확도를 평가한다.

혼동 행렬은 다음과 같이 4개의 항목으로 구성된다.

True Positive(TP): 실제값이 양성(Positive)이고, 모델이 예측한 값도 양성(Positive)인 경우
False Positive(FP): 실제값이 음성(Negative)이고, 모델이 예측한 값은 양성(Positive)인 경우
False Negative(FN): 실제값이 양성(Positive)이고, 모델이 예측한 값은 음성(Negative)인 경우
True Negative(TN): 실제값이 음성(Negative)이고, 모델이 예측한 값도 음성(Negative)인 경우

이 4개의 항목을 바탕으로 혼동행렬은 다음과 같이 구성된다.

	Actual Positive	Actual Negative
Predicted Positive	True Positive(TP)	False Positive(FP)
Predicted Negative	False Negative(FN)	True Negative(TN)

예를 들어, 스팸 메일 분류기에서 스팸 메일을 양성(Positive), 일반 메일을 음성(Negative)으로 분류한다고 가정한다.

스팸 메일 분류기가 100개의 이메일을 분류하여 혼동행렬을 구한 결과가 다음과 같다.

	Actual Positive	Actual Negative
Predicted Positive	80	10
Predicted Negative	5	5

위 혼동행렬에서는 TP가 80, FP는 10, FN은 5, TN은 5가 된다.
이를 바탕으로 정확도, 정밀도, 재현율 등의 평가 지표를 계산할 수 있다.

앙상블

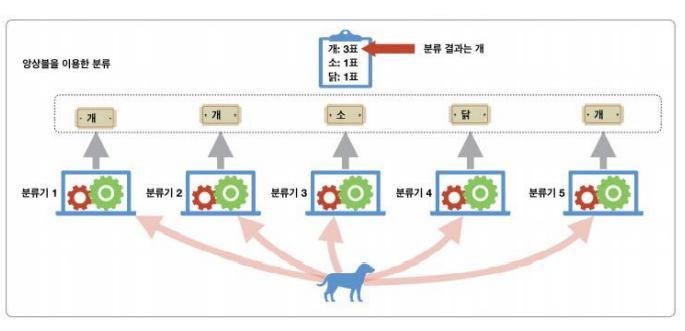
여러 가지 종류의 분류기를 개선하는 데에 한계가 있을 때, 이들의 협력을 이용하는 방법

머신러닝이 어느 수준의 성능에 도달하면 분류기를 개선하는 일이 어려워진다.
모델의 특성에 따라 일정 수준 이상의 성능을 넘어서는 것도 어려우며, 이를 해결하기 위한 기법이 앙상블 기법이다.

분류기의 성격이 모두 동일해 오분류도 비슷한 상항이 일어날 경우 모두가 한꺼번에 잘못된 투표를 할 확률이 높아진다.
- 이럴 경우 모델의 성격이 서로 다른 것이 좋다.
- 이를 개별 분류기의 다양성이라고 한다.
분류기의 다양성을 확보하는 방법 ?
1. 서로 다른 모델로 각각의 분류기 만들기.
2. 각각의 분류기에 대해 서로 다른 학습 데이터를 제공하여 훈련.
분류기에 선택된 데이터가 다른 분류기의 학습에도 사용될 수 있다면 이를 배깅(Bagging) 기법이라고 한다.
- 불가능할 경우 페이스팅(Pasting) 이라고 한다.
- 확률 통계 분야에서 이러한 추출을 각각 복원 추출, 비복원 추출이라고 한다.
- 배깅 기법을 개선한 방법이 부스팅 기법이다.

부스팅 알고리즘은 Ada Boost 알고리즘이 가장 일반적으로 사용된다.

`Ada Boost`

✅ 특징

각 데이터가 인스턴스는 동일한 가중치로 초기화한다.
예측기를 순차적으로 학습시킨다.
한 예측기가 잘못 분류한 데이터 인스턴스의 가중치를 높인다.
다음 예측기는 높은 가중치의 데이터 인스턴스에 적합하게 학습한다.

군집화(Clustering)

💡 소속집단의 정보가 없고 모르는 상태에서 비슷한 집단으로 묶는 비지도 학습.

입력 데이터를 바탕으로 출력값을 예측하는 목적으로 사용한다기 보단, 데이터에서 의미를 파악하고 기준을 만드는 목적으로 사용한다.

군집화 분석에서 가장 일반적으로 사용되는 알고리즘은 K-Means 알고리즘이다.

K-Means 알고리즘은 다음과 같은 과정을 거친다.

사용자는 분석하려는 데이터에서 클러스터 개수 k를 정한다.
임의의 k개의 중심점을 선택한다. 이러한 중심점은 각 클러스터의 중심이 되는 점으로, 초기화 단계에서는 무작위로 선택된다.
각 데이터 포인트에서 가장 가까운 중심점을 찾아 해당 중심점과 연결된 클러스터에 해당 데이터 포인트를 할당한다.
클러스터에 할당된 모든 데이터 포인트의 평균을 계산해 새로운 중심점을 구한다.
새로운 중심점을 기반으로 클러스터를 다시 할당한다. 즉, 3번 과정부터 다시 반복한다.
클러스터 할당이 변하지 않을 때 까지 3-5번의 과정을 반복한다.

✅ 특징

K-Means 알고리즘은 중심점의 위치를 초기에 무작위로 선택한다.
이로 인해 실행할 때 마다 다른 결과가 나올 수 있다.
해당 알고리즘은 클러스터 개수를 사용자가 정해줘야 하기 때문에 적절한 값을 찾는 것이 중요하다.

요약 ✅

정밀도와 재현율은 트레이드 오프가 존재한다.
즉 하나를 높이면 다른 하나는 낮아지는 현상이 발생한다.

앙상블 기법은 다수의 분류기가 협력해 전체적인 분류 성능을 높이는 기법이다.

앙상블을 구성하는 분류기는 동질성을 갖는 것보다 다양성을 갖는 것이 좋다.

분류기의 다양성을 확보하기 위해 서로 다른 학습 데이터를 재공하는 배깅 과 페이스팅이 사용된다.

배깅과 페이스팅의 구분은 데이터를 복원 추출하냐, 비복원 추출하냐의 차이다.

부스팅은 분류기를 순차적으로 학습하며 이전 분류기가 제대로 처리하지 못 한 데이터에 더 집중하는 기법이다.

군집화란, 소속집단의 정보가 없고 모르는 상태에서 비슷한 집단으로 묶는 비지도 학습중 하나이다.

K - Means 알고리즘은 군집의 개수에 따라 데이터를 군집으로 분류하는 알고리즘으로 원리가 단순하고 직관적이며 성능이 좋은 군집화 알고리즘이다. 사전에 군집의 개수 K를 지정해 줘야 한다.

Jae Chan

🐋

이전 포스트

머신러닝 - 분류와 군집화

TIL

`K-NN` 알고리즘

표집 편향과 성능 측정을 위한 평가지표

정확도 (Acc)

재현율 (Recall)

정밀도 (Precision)

혼동행렬(Confusion Matrix)

앙상블

`Ada Boost`

군집화(Clustering)

요약 ✅

머신러닝 - 회귀(Regression)

0개의 댓글