머신러닝의 탐색과 최적화에 대한 내용입니다.
상태 공간과 탐색
-
🔍 탐색(Search)
문제의해(Solution)가 될 수 있는 것들의 집합을 공간으로 간주하며,
문제에 대한 최적의 해를 찾기 위해 공간을 체계적으로 찾아보는 것 -
💡 해(Solution)
일련의 동작으로 구성되거나 하나의 상태로 구성된다. -
상태(State)
특정 시점에 문제의 세계가 처해 있는 모습이다. -
세계(World)
문제에 포함된 대상들과 이들의 상황을 포괄적으로 지칭 -
상태 공간(State space)
문제 해결 과정에서 초기 상태로부터 도달할 수 있는 모든 상태들의 집합을 의미.
문제의 해가 될 가능성이 있는 모든 상태들의 집합이다.- 초기 상태(Initial State) : 문제가 주어진 시점의 시작 상태
목표 상태(Goal State) : 문제에서 원하는 최종 상태
- 초기 상태(Initial State) : 문제가 주어진 시점의 시작 상태
-
상태 공간 그래프(State space Graph)
상태공간에서 각 행동에 따른 상태의 변화를 나타낸 그래프이다.- 노드 :
상태 - 링크 :
행동
- 노드 :
다음은 탐색의 종류들이다.
- 맹목적 탐색 (Blind Search)
- 정보 이용 탐색 (Informed Search)
- 게임 탐색 (Game Search)
맹목적 탐색
💡 어떤 문제에 대한 해를 찾기 위해 모든 가능한 상태나 선택지를 탐색하는 방법.
깊이 우선 탐색(DFS)
- 깊이 우선 탐색 (Depth-First-Search)
정해진 순서에 따라 상태 공간 그래프를 점차 생성해 가면서 해를 탐색하는 방법이다.
현재 정점에서 아직 방문하지 않은 자식 노드 중 하나를 선택해 재귀적으로 탐색한다.
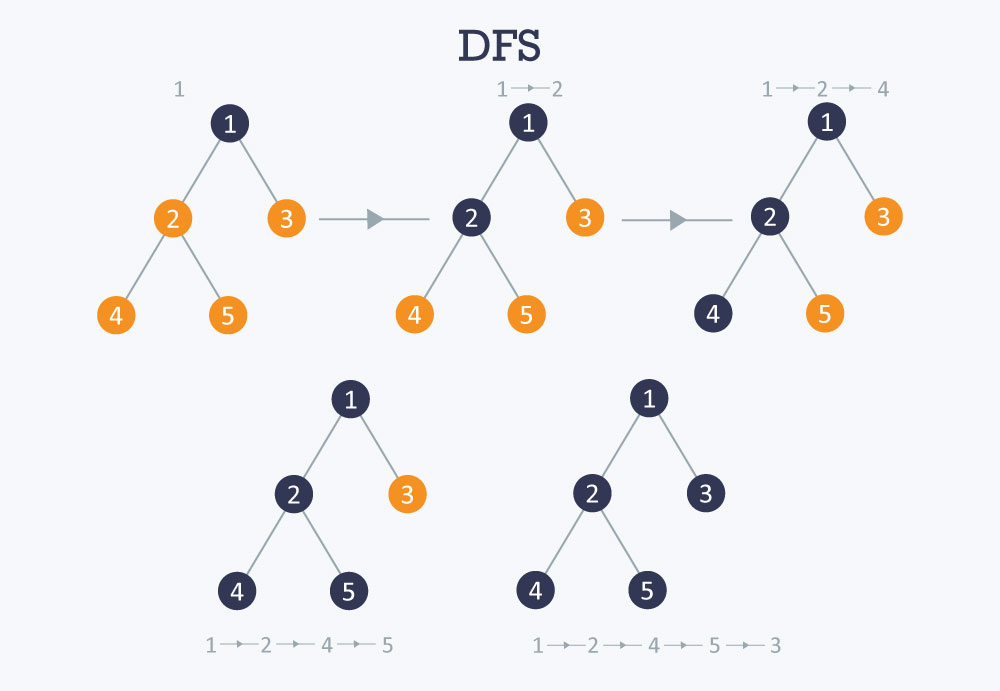
✅ 특징
- 초기 노드로부터 시작해 깊이 방향으로 탐색한다.
- 목표 노드에 도달하면 종료된다.
- 더 이상 방문할 수 있는 자식 노드가 없게 되면 이전 단계로 돌아가 다른 자식 노드를 탐색한다. 이렇게 전체 공간을 빠짐없이 체크하며 해를 찾는다.
→백 트래킹 (Back-Tracking) - 메모리 사용량이 적고 구현하기 쉬우며 최적의 해를 찾지 못할 가능성이 있으나
해가 존재할 경우 빠르게 찾을 수 있다. - 해가 깊은 단계에 있는 경우에 이후 설명할 BFS보다 빠르게 찾을 수 있다.
❌ 단점
- 무한 루프에 빠질 가능성이 있다.
- 최적의 해가 보장되지 않기 때문에 모든 경우의 수를 탐색하지 못할 수도 있다.
- 문제가 복잡할수록 실행 시간이 길어질 수 있다.
따라서 간단한 문제에는 유용하게 사용이 되지만, 복잡한 문제에 대해서는 옳지 않은 방법이기에 다른 탐색 방법을 고려해야함.
너비 우선 탐색(BFS)
💡 초기 노드에서 시작하여 인접한 모든 자식 노드를 탐색하는 방법.
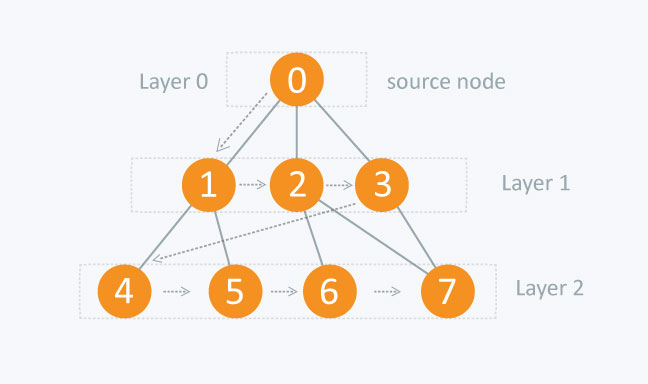
✅ 특징
- 루트 노드에서 인접한 모든 노드를 탐색한 뒤 그 다음 레벨의 노드를 탐색한다.
- 큐(
Queue) 자료구조를 사용해 구현된다.- 시작 노드를 큐에 넣는다.
- 큐에서 노드를 하나씩 꺼내며 해당 노드의 자식들을 큐에 넣는다.
- 이후, 큐에서 노드를 꺼내며 다음 레벨의 노드를 탐색한다.
- 이 과정을 계속 반복한다.
- 깊이 우선 탐색(DFS)과는 달리 최단 경로를 보장한다.
- 최소 비용 문제 또는 노드 간의 최단 거리를 찾을 때 유용하다.
- 어떠한 노드의 발견되는 순서가 중요한 경우 유용하다.
❌ 단점
- 메모리 사용량이 크며, 문제가 복잡할수록 실행 기간이 길어질 수 있다.
- 해가 깊은 단계에 있는 경우에는 DFS보다 탐색이 느릴 수 있다.
복잡한 문제에 대해서 실행 기간과 메모리 사용량이 너무 크기 때문에 사용이 제한되며,
최단 경로나 최단 거리를 구해야 할 때 유용한 알고리즘이다.
반복적 깊이 심화 탐색(IDDFS)
💡 IDDFS ( Iterative Deepening Depth-First Search )
- 깊이 우선 탐색의 장점을 살리면서 단점을 보완한 탐색 알고리즘이다.
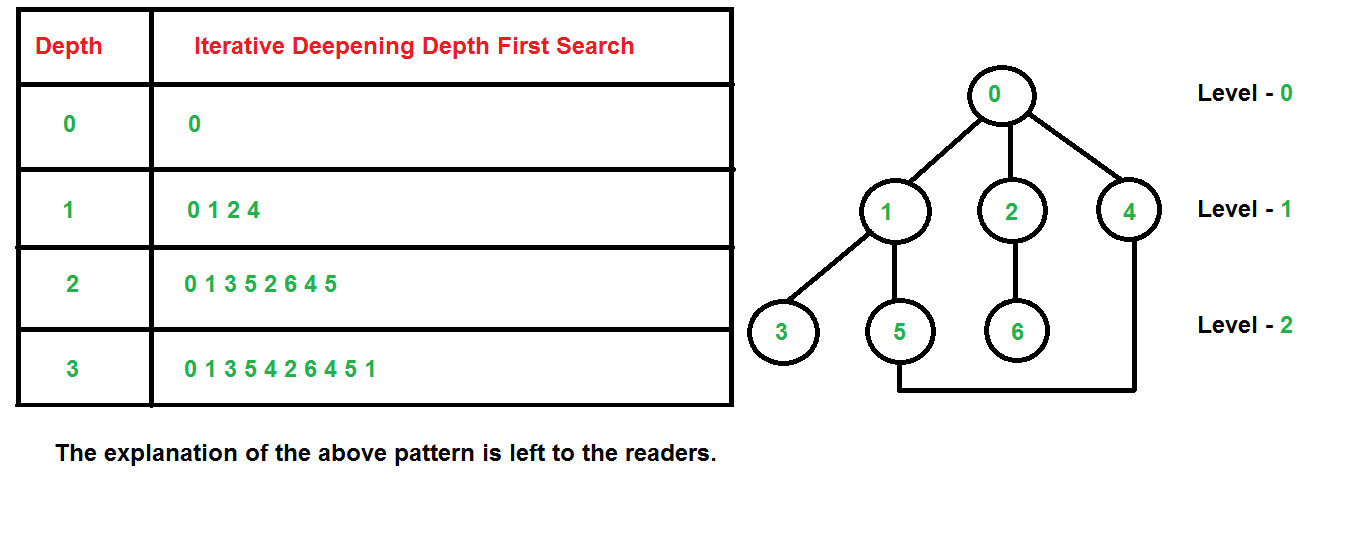
동작 방식
- 깊이 제한을 1로 설정한다.
- 루느 노트를 스택에 넣는다.
- 스택에서 노드를 하나씩 꺼내어 해당 노드의 자식 노드들을 스택에 넣는다.
- 스택이 빌 때 까지 3번 과정을 반복한다.
- 탐색이 끝나지 않았을 경우, 깊이 제한을 1 증가 시킨후 2-3번을 반복한다.
- 탐색이 끝나지 않았을 경우, 5번을 반복한다.
✅ 특징
- 깊이 우선 탐색과 마찬가지로 모든 노드를 방문한다.
- DFS와는 달리 깊이 제한을 두어 메모리 사용 제한이 가능하며 BFS보다 메모리 사용량이 적다.
양방향 탐색(BS)
💡 시작 노드와 목표 노드에서 동시에 탐색을 시작하며 두 노드가 만나는 시점에 탐색을 종료한다.

✅ 특징
- 단방향 탐색 알고리즘보다 빠르게 최단 경로를 찾을 수 있다.
- 탐색이 동시에 시작되기 때문에 두 노드가 만나는 지점에서 탐색이 종료 되므로,
탐색 시간 단축이 가능하다.
맹목적 탐색 방법들을 비교해보면 이와 같다.
-
깊이 우선 탐색(DFS)
✅ 메모리 공간 사용 효율적
❌ 최단 경로 해 탐색 보장 불가. -
너비 우선 탐색(BFS)
❌ 메모리 공간 사용 비효율적
✅ 최단 경로 해 탐색 보장. -
반복적 깊이심화 탐색(IDDFS)
✅ 최단 경로 해 보장.
✅ 메모리 공간 사용 효율적.
✅ 맹목적 탐색의 필요 시 우선 적용 고려 대상이다.
정보이용 탐색(Informed Search)
💡 최적의 해를 찾기 위해 가능한 경우의 수를 전부 탐색하는 것이 아닌, 문제의 도메인 지식을 이용해 최적의 해를 찾기 위한 탐색 전략을 수립하는 것이다.
탐색의 종류로 다음과 같다.
- 휴리스틱 탐색(Heuristic Search)
- 언덕 오르기 방법
- 빔 탐색
- A* 알고리즘
- 휴리스틱(Heuristic)
시간이나 정보가 불충분해 합리적인 판단을 할 수 없거나, 굳이 체계적이고 합리적인 판단을 할 필요가 없는 상황에서 신속하게 어림짐작 하는 것을 의미한다.
언덕 오르기 방법(Hill Climbing Method)
✅ 특징
- 현재 노드에서 휴리스틱에 의한 평가값이 가장 좋은 이웃 노드 하나를 확장해 가는 탐색 방법이다.
- 더 이상 개선할 수 없는 지점(지역 최적해)에 도달하면 탐색을 중단한다.
- 지역 최적해에 빠질 가능성이 있다.

최상 우선 탐색(Best-First Search)
💡 경로 탐색에서 현재 상태에서 목표 상태까지 가는 경로를 찾기 위해 우선순위 큐를 사용하는 탐색 알고리즘이다.
✅ 특징
- 확장 중인 노드들 중에서 목표 노드까지 남은 거리가 가장 짧은 노드를 확장하여 탐색한다.
- 남은 거리를 정확히 알 수 없으므로 휴리스틱을 사용한다.
빔 탐색(Beam Search)
💡 휴리스틱에 의한 평가값이 우수한 일정 개수의 확장 가능한 노드만을 메모리에 관리하며 최상 우선 탐색을 적용하는 알고리즘.

A* 알고리즘
💡 너비 우선 탐색과 최상 우선 탐색의 장점을 모두 취하면서도 비용이 가장 적게 드는 경로를 찾는 알고리즘이다.
✅ 특징
- 시작점에서부터 목표점까지의 최단 경로를 찾기 위해, 각 경로에 대한 추정 비용과 실제 비용을 모두 고려한다.
즉, 시작점에서부터 목표점까지의 경로가 트리를 형성한다면, A* 알고리즘은 시작점에서 목표점까지의 경로 중에서 최단 경로를 찾기 위해 시작점에서 각 노드까지의 실제 비용과 목표점까지의 추정 비용을 더한 값을 기준으로 우선순위 큐에 저장해 탐색한다.
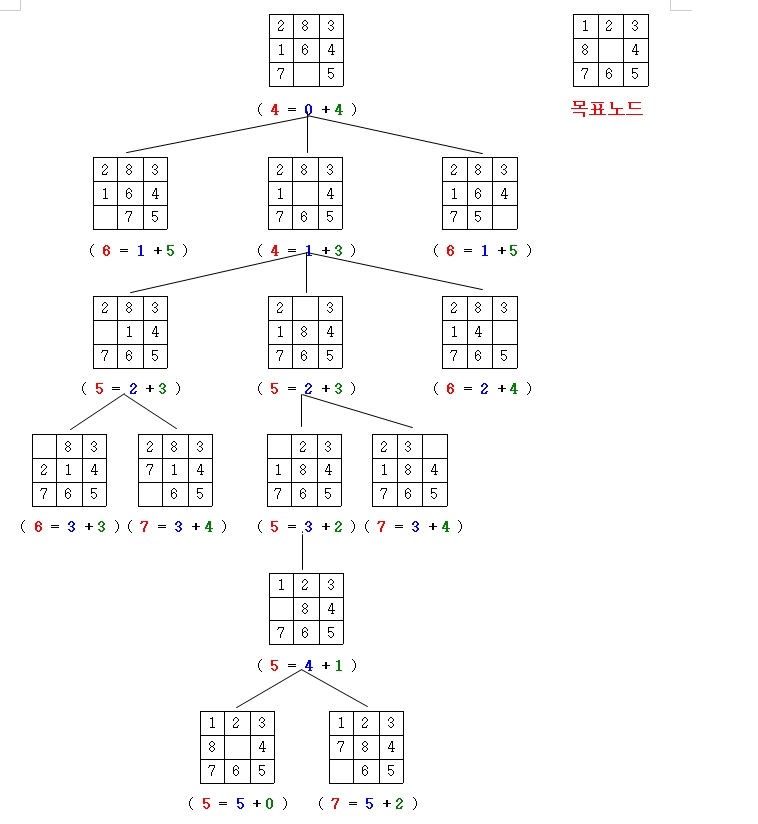
게임 탐색
🎮 게임에서 가능한 모든 상태를 탐색해 가장 좋은 결정을 내리는 알고리즘이다.
보통 상대방이 취할 수 있는 모든 수를 미리 예측하고, 각각의 수에 대해 가능한 모든 게임 상태를 예측하며 이러한 상태들은 일반적으로 게임 트리라고 불리는 트리 구조를 형성한다.
💡 게임 트리란?
→ 상대가 있는 게임에서 자신과 상대방의 가능한 게임 상태를 나타낸 트리
대표적인 탐색 종류
- Mini-Max 알고리즘
- 몬테카를로 시뮬레이션
Mini-Max 알고리즘
턴 기반 게임에서 보통 사용된다.
작동 방식
- 게임 트리를 탐색하며 각각의 턴에서 상대방이 최선의 선택을 할 것이라 가정한다.
- 자신의 턴에서는 최대한 상대방이 자신에게 불리한 선택을 할 수 없도록 최선의 선택을 한다.
이 과정을 미니맥스 알고리즘이라고 부른다.
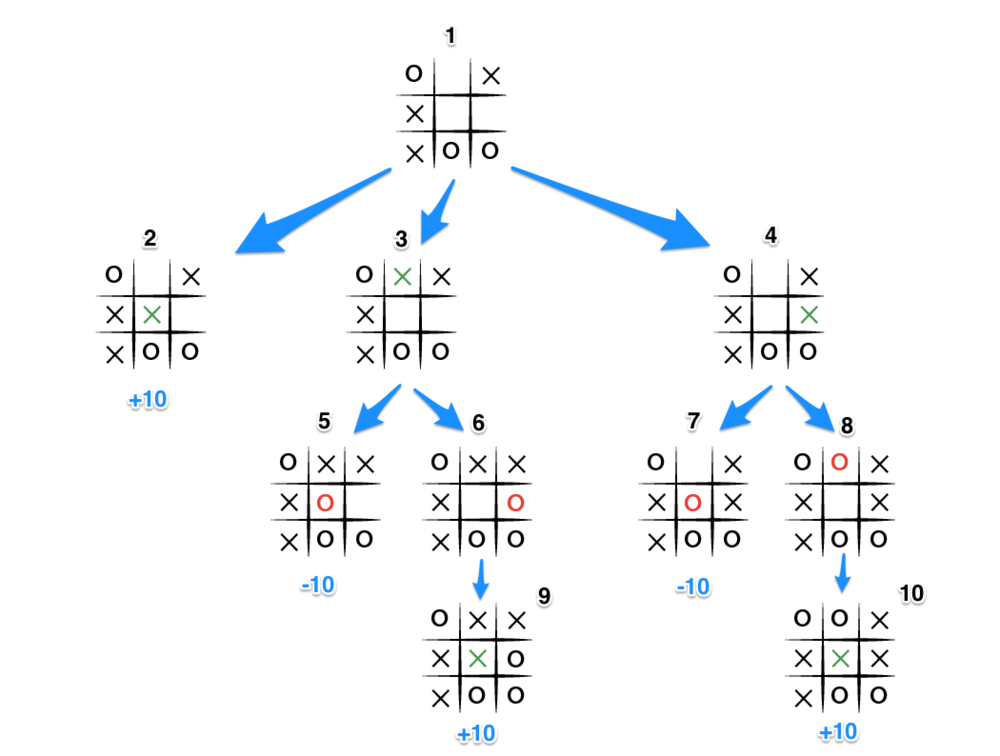
✅ 특징
- 게임 트리를 모두 탐색할 수 없기 때문에, 트리 탐색을 제한하는 가지 치기 알고리즘을 적용한다.
- 가지치기 알고리즘을 통해 계산을 줄이며 게임 트리를 깊이 탐색할 수 있게 한다.
미니맥스 알고리즘은 게임 이론에서 중요하게 여기며, 미니맥스 알고리즘을 기반으로 한 많은 다른 알고리즘이 개발되어왔다.
몬테카를로 시뮬레이션
💡 미니맥스 알고리즘과 같이, 게임을 플래이하며 가장 높은 수를 찾는 방법 중 하나이다.
✅ 특징
- 특정 확률 분포로부터 무작위 난수나 표본을 생성한다.
- 이 표본에 따라 행동을 하는 과정을 반복해 결과를 확인한 후, 결과확인 과정을 반복해 최종 결정을 한다.
몬테카를로 트리 탐색(MCTS)
💡 탐색 공간을 무작위 표본추출을 하며, 탐색트리를 확장해 가장 좋아 보이는 것을 선택하는 휴리스틱 탐색 방법이다.
4개 단계를 반복하며 시간이 허용하는 동안 트리 확장과 시뮬레이션을 한다.
- 선택 (Seleciton)
- 확장 (Expansion)
- 시뮬레이션 (Simulation) → 몬테카를로 시뮬레이션
- 역전파 (Back Propagation)
제약조건 만족 문제
💡 주어진 제약조건을 만족하는 조합 해(Combinatorial Solution)를 찾는 문제이다.
탐색 기반의 해결방법으로는
- 백트랭킹 탐색
- 제약조건 전파
등이 있다.
백트랙킹 탐색(Backtracking Search)

✅ 특징
- 깊이 우선 탐색을 하는 것처럼 변수에 허용되는 값을 하나씩 대입한다.
- 모든 가능한 값을 대입하며 만족하는 것이 없으면 이전 단계로 돌아가 이전 단계의 변수에 다른 값을 대입한다.
제약조건 전파
✅ 특징
- 인접 변수 간의 제약 조건에 따라 각 변수에 허용될 수 없는 값들을 제거하는 방식이다.
최적화
💡 최적화란 ?
여러 가지 혀용되는 값들 중에서 주어진 기준을 가장 잘 만족하는 것을 선택하는 것이다. 최적화의 종류로는 조합 최적화와 함수 최적화가 있다.
-
조합 최적화의 종류
- 유전 알고리즘
- 메타 휴리스틱
-
함수 최적화의 종류
- 함수 최적화 문제
- 제약조건 최적화
- 경사하강법
-
목적함수(
Objective Function)
최소 또는 최대가 되도록 만들려는 함수이다.
