[Algorithm] 가장 먼 노드 _ dijkstra

문제 설명

n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.

노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.

제한사항

노드의 개수 n은 2 이상 20,000 이하입니다.
간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.

입출력 예

n 6
vertex [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]]
return 3

입출력 예 설명

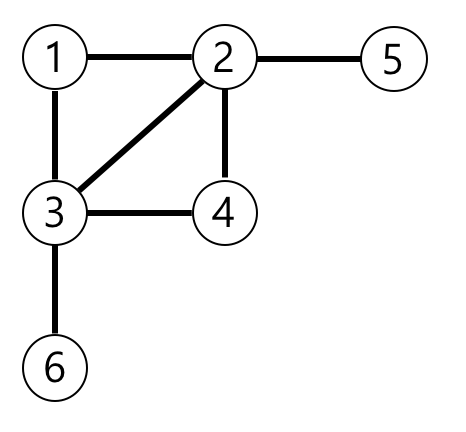
예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.

---

접근하기

• 그래프를 이용하는 문제였다.
• 1번으로부터 가장 먼 노드의 갯수를 찾는 문제이다.
• 1을 제외한 모든 노드의 가중치를 1로 두고 다익스트라 알고리즘을 수행하면 각 노드별로 최소 거리로 갈 수 있는 가중치 값들이 구해진다.
• 그 값들 중, 최대 값을 찾아서 그 갯수를 리턴하면 된다.

Code

import java.util.*;
class Solution {
    class Edge implements Comparable<Edge>{
        int to, weight;
        Edge(int to, int weight){
            this.to = to;
            this.weight = weight;
        }
        @Override
        public int compareTo(Edge e){
            return this.weight - e.weight;
        }
    }
    
    PriorityQueue<Edge> pq;
    ArrayList<ArrayList<Edge>> adj;
    int[] dist;
    
    public int solution(int n, int[][] edge) {
        int answer = 0;
        pq = new PriorityQueue<>();
        adj = new ArrayList<>();
        dist = new int[n+1];
        
        Arrays.fill(dist,Integer.MAX_VALUE);
        for(int i=0; i<=n; ++i) adj.add(new ArrayList<>());
        
        for(int i=0; i< edge.length; ++i){
            int from = edge[i][0];
            int to = edge[i][1];
            int weight = 1;
            
            adj.get(from).add(new Edge(to, weight));
            adj.get(to).add(new Edge(from, weight));                
        }
        
        dist[1] = 0;
        pq.offer(new Edge(1,0));
        
        dijkstra();
        
        int max = 0;
        for(int a: dist){            
            if(a<=n){
                if(max<=a){
                    max = a;
                }
            }
        }
        
        for(int a : dist){
            if(a==max) answer++;
        }
        
        return answer;
    }
    
    public void dijkstra(){
        while(!pq.isEmpty()){            
            Edge e = pq.poll();
            for(Edge ne : adj.get(e.to)){
                if(dist[ne.to] > dist[e.to] + ne.weight){
                    dist[ne.to] = dist[e.to] + ne.weight;
                    pq.offer(ne);
                }
            }
        }
    }
}

✅

• 다익스트라를 이용하면 쉬운 문제였다.