[OS] 페이징

Intro

외부 단편화로 인한 메모리 낭비가 심하다.
Compaction을 사용하면 외부 단편화를 해결 할 수 있지만 오히려 이로인해 발생하는 오버헤드, 비효율적인 성능으로 사용하기 어렵다.
그래서 나온게 페이징이다.
hole을 가지고 해결하려 하지 않고 프로세스를 작은 단위로 나눠서 외부 단편화를 해결하려 한다.

페이징

• 프로세스를 일정한 작은 크기로 나누고, hole 역시 같은 크기로 나눈다.
• 이러한 작은 조각들의 크기에 맞춰 메모리에 할당한다.

🧐 하지만, 하나의 프로세스는 연속적인 동작을 수행하는데 이를 작은 여러 조각으로 나누면 프로세스가 정상적으로 동작할까?

다중 프로그래밍에서 살펴봤던 개념처럼 MMU를 통해 논리 주소와 물리주소를 나눠 사용하고 이를 MMU가 재배치 해주는 작업을 해준다고 하였다.
이 역시 CPU를 속이는 행동이다.
실제로 메모리는 전혀 연속적이지 않은데, CPU는 연속적으로 사용하고 있다는 것을 보장받으며 수행한다.

50byte크기의 프로세스가 있다고 하자. 페이징의 크기는 각 10byte로 나눈다.

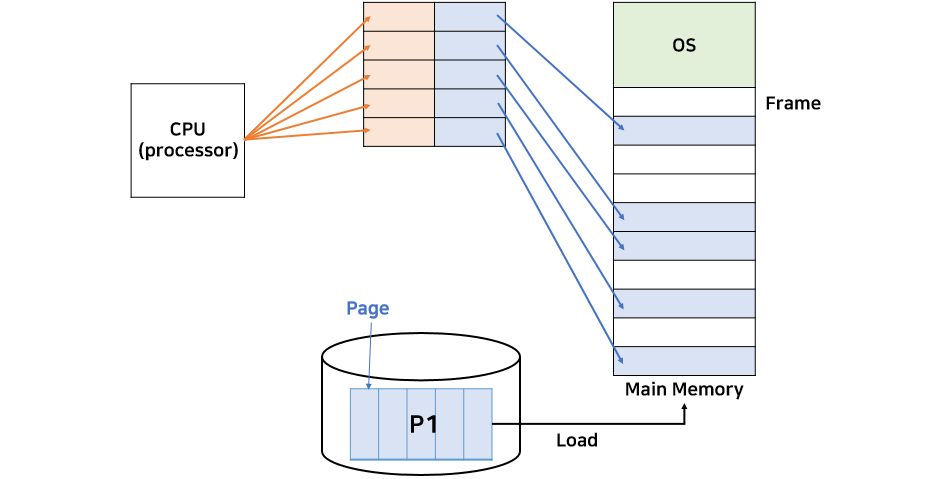
위 그림과 같이 P1은 5개의 페이지로 나눌 수 있다.
이를 메인 메모리 5곳에 나눠 할당한다.
CPU는 논리 주소로 프로그램이 설정한대로 연속적인 주소값으로 명령을 내리고 이는 메모리로 가기전에 각 페이지의 실제 메모리 주소가 저장되어 있는 테이블에서 물리주소로 변경되어야 한다.

프로세스를 나눈 조각을 page라고 하고, 메모리를 나눈 조각을 frame이라고 한다.
프로세스는 페이지의 집합이고, 메모리는 프레임의 집합이다.

프로세스를 정상적으로 사용하기 위해 MMU의 재배치 레지스터를 여러 개 사용하여 위의 그림처럼 각 페이지의 실제 주소로 변경해준다.

이러한 여러 개의 재배치 레지스터를 페이지 테이블이라 한다.

주소 변환

• 페이징 기법을 사용하기 위해 여러 개로 흩어진 페이지에 CPU가 접근하기 위해서 페이지 테이블을 통해 주소를 변환해야 한다.

논리 주소

CPU가 내는 주소는 2진수로 표현되고 이를 m비트가 있다고 가정하자.
여기서 하위 n비트는 오프셋 또는 변위라고 한다.
그리고 상위 m-n 비트는 페이지의 번호에 해당한다.
(n = d, m-n = p) 이렇게만 보면 이해가 안되니 예제로 보자.

페이지 번호(p)는 페이지 테이블의 인덱스 값.
p에 해당하는 테이블 내용은 메모리의 프레임 번호!

• Page Size = 16bytes
• Page Table : 5, 3, 2, 8 , 1, 4
• 논리 주소 50번지는 물리 주소 몇 번지 인가?

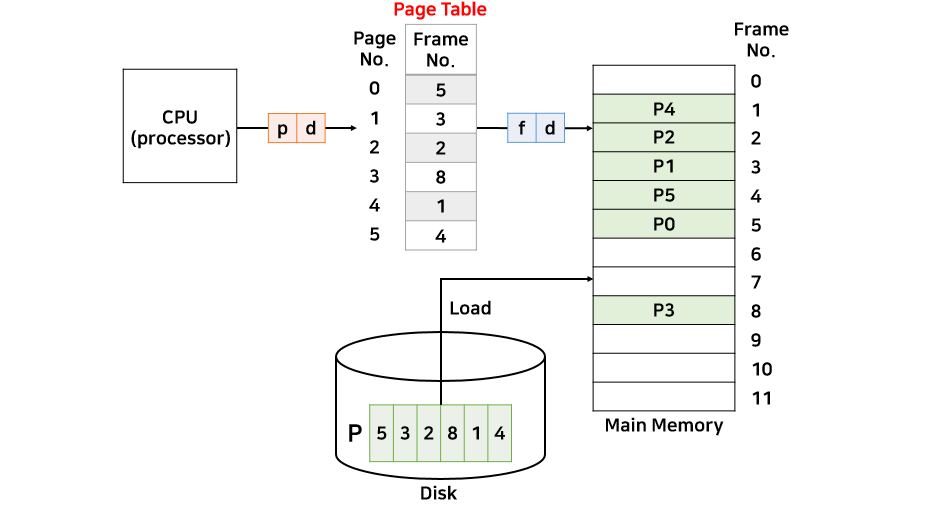
위 그림은 프로세스 P가 메모리에 할당된 모습이다.
CPU가 50번지에 접근하려 한다.
그러면 페이지 테이블의 정보를 읽어오기 위해 논리주소를 p,d로 나눠야 한다.

d는 페이지 크기에 따라 달라지는 데, Page Size가 16byte이니까 2^4이다.
그래서 d = 4가 되므로 이진수의 뒤에서 4칸이 d이다.

50 = 110010
p = 11
d = 0010

P는 이진수로 11이고 십진수로 3이다.
즉, 페이지 테이블의 페이지 번호 3을 가리킨다.
페이지 3번에 해당하는 프레임번호는 8이므로 물리주소를 구성하는 f값은 8이 된다.

f = 1000
d = 0010
물리주소 = 10000010

최종적으로 물리주소는 f,d로 구성되어 있으므로 물리주소는 이진수로 10000010이 되고, 십진수로는 130번지가 된다.
즉, 변위는 2이므로 8번재 프레임의 시작주소는 128번지가 된다.

연속 메모리 할당을 하면서 외부 단편화가 발생하여 이를 해결하기 위해 페이징이 나왔다.
하지만 페이징은 외부 단편화가 아닌 내부 단편화가 발생한다.

내부단편화

• 프로세스 크기가 페이지 크기의 배수가 아닐 경우, 마지막 페이지는 한 프레임을 다 채울 수 없다.
• 이로 인한 공간 발생은 메모리 낭비로 이어진다.

예를 들어, 15byte 크기의 프로세스 P가 있다.
페이지 크기(프레임 크기)는 4byte로 P를 페이지로 나누면 4,4,4,3의 크기로 총 4개의 페이지가 만들어진다.
여기서 마지막 3byte 페이지는 프레임 크기보다 1byte 작으므로, 이 만큼 메모리 공간이 비게 된다.
이렇게 비어진 공간은 프로세스 P에서도 쓰지 않고, 다른 프로세스에서도 쓰지 못하는 낭비되는 공간이 된다.

내부단편화는 해결 방법이 없다. 😹
하지만 내부단편화는 외부단편화에 비해 낭비되는 메모리 공간은 매우 적다.
내부 단편화의 최대 낭비되는 크기는 page size - 1이 된다.
(외부 단편화는 최대 전체 메모리의 1/3이 낭비된다고 이전에 살펴봤다)
이는 무시할 정도로 작은 크기다.

페이지 테이블 만들기

• CPU 내부에 페이지 테이블을 만들 수 있다.
  CPU 내부의 기억장치는 레지스터로 여러개의 레지스터로 페이지 테이블을 만드는 것.
  CPU 내부에 페이지 테이블을 만들면, 장점은 주소 변환 속도가 빠르다. 하지만 단점은 CPU 내부에 사용할 수 있는 레지스터는 한정되어 있어 페이지 테이블의 크기가 매우 제한된다.

• 페이지 테이블을 메모리 내부에 만들 수도 있다.
  메모리 내부에 만드는 것의 장단점은 CPU와 정반대이다.
  즉, 장점은 페이지 테이블의 크기 제한이 없는 것이고 단점은 주소 변환 속도가 느리다는 것이다.
  CPU는 프로세스의 주소에 접근하기 위해 메모리에 위치한 페이지 테이블에 한 번, 실제 주소로 접근하는데 한 번해서 메모리에 총 2번 접근해야 하므로 속도가 2배 느려진다.

이 모든 것을 해결하기 위해 페이지 테이블도 캐시로 만들어 해결한다.
페이지 테이블을 별도의 칩(SRAM)으로 만들어서 CPU와 메모리 사이에 위치시킨다.
이러한 테이블을 TLB(Translation Lock-aside Buffer) 라고 부른다.

👍 CPU보다 변환 속도가 느리고 메모리보다 테이블 크기는 작지만, CPU보다 테이블 크기가 크고 메모리 보다 변환 속도가 빠르다.

TLB는 캐시와 역할이 동일하므로, 실제 전체 페이지 테이블은 메모리에 위치해 있고 테이블의 일부를 TLB에 가져와서 사용한다.
TLB에 유효한 페이지가 있을 때와 없을 때의 속도차이가 발생한다.

TLB 효율을 알아보기 위해 Effective Memory Access Time을 계산해보자.

• 메모리를 읽는 시간(Tm) = 100ns
• TLB를 읽는 시간(Tb) = 20ns
• TLB에 유효한 페이지 엔트리가 있을 확률(hit ratio) = 80%

먼저, EMAT의 정형화된 식을 보자.

EMAT = h(Tb + Tm) + (1-h)(Tb + Tm + Tm), h는 hit ratio

예제를 계산해보면 140ns가 나온다.
hit ratio는 실제로 평균 95%이상이므로 충분히 효율적으로 동작한다고 볼 수 있다.

실제 유효한 메모리에 접근하는 시간은 위와 같다. TLB에 유효한 페이지가 있다면 TLB를 읽는 시간과 실제 메모리를 읽는 시간만 있으면 된다.
하지만, TLB에 유효한 페이지가 없다면 이를 다시 메모리에서 가져와야 하므로 메모리를 총 2번 읽어야 한다.

Ref

• KOCW 운영체제 강의