[코딩 테스트] - 소수 판별 알고리즘, 에라토스테네스의 체

소수 판별 알고리즘

• 소수: 1보다 큰 자연 수 중 1과 자기 자신을 제외한 자연수로는 나누어떨어지지 않는 자연수
• 어떠한 자연수가 소수인지 아닌지 판별하는 문제가 자주 출제됨
• 기본 코드

  import math
  
  # 소수 판별 함수
  def is_prime_number(x):
      # 2부터 x-1 까지의 모든 수를 확인하며
      for i in range(2, x):
          # x가 해당 수로 나누어떨어진다면
          if x % i == 0:
              return False # 소수가 아님
      return True # 소수임
  
  print(is_prime_number(4)) # 4는 소수가 아님
  print(is_prime_number(7)) # 7은 소수임

• 소수 판별 알고리즘의 시간 복잡도
  • 2부터 X-1까지의 모든 자연수에 대하여 연산을 수행해야 하므로 모든 수를 하나씩 확인한다는 점에서 시간 복잡도는 O(X)
• 약수의 성질
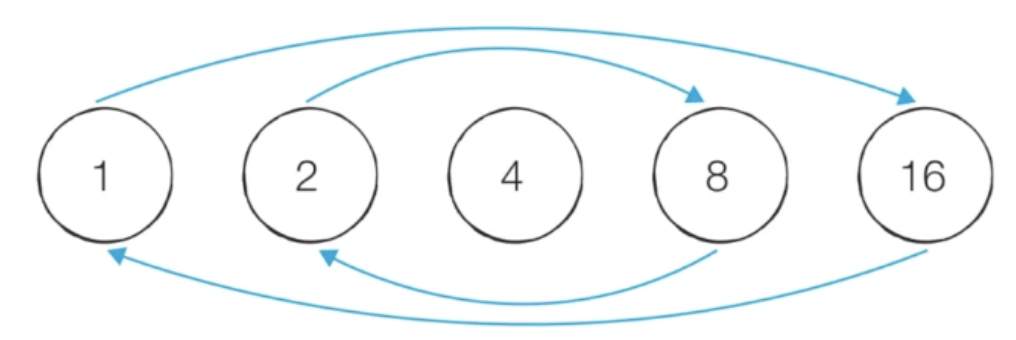
  • 모든 약수가 가운데 약수를 기준으로 곱셈 연산에 대해 대칭을 이룸
    • ex) 16의 약수는 1, 2, 4, 8, 16
    • 2 x 8 = 16은 8 x 2 = 16과 대칭
  • 따라서 특정한 자연수의 모든 약수를 찾을 때 가운데 약수(제곱근)까지만 확인하면 됨

    • ex) 16이 2로 나누어떨어진다는 것은 8 로도 나누어떨어진다는 것을 의미

      

• 개선된 코드(제곱근까지 확인)

  import math
  
  # 소수 판별 함수
  def is_prime_number(x):
      # 2부터 x의 제곱근까지의 모든 수를 확인하며
      for i in range(2, int(math.sqrt(x)) + 1):
          # x가 해당 수로 나누어떨어진다면
          if x % i == 0:
              return False # 소수가 아님
      return True # 소수임
  
  print(is_prime_number(4)) # 4는 소수가 아님
  print(is_prime_number(7)) # 7은 소수임

• 개선된 알고리즘의 시간복잡도
  • 2부터 X의 제곱근(소수점 이하 무시)까지의 모든 자연수에 대하여 연산을 수행해야 하므로 시간복잡도는 O(N^1/2)

에라토스테네스의 체

• 특정한 수의 범위 안에 존재하는 모든 소수를 찾아야할 떄 에라토스테네스의 체 알고리즘을 사용함

• 다수의 자연수에 대하여 소수 여부를 판별할 때 사용하는 대표적인 알고리즘

• N보다 작거나 같은 모든 소수를 찾을 때 사용

• 동작과정

  1. 2부터 N까지의 모든 자연수 나열
  2. 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i 찾기
  3. 남은 수 중에서 i의 배수 모두 제거 (i는 제거하지 않음)
  4. 더 이상 반복할 수 없을 때까지 2번과 3번의 과정을 반복함
  • [초기 단계] 2부터 26까지의 모든 자연수 나열 (N = 26)
  • [Step 1] 아직 처리하지 않은 가장 작은 수 2를 제외한 2의 배수 모두 제거
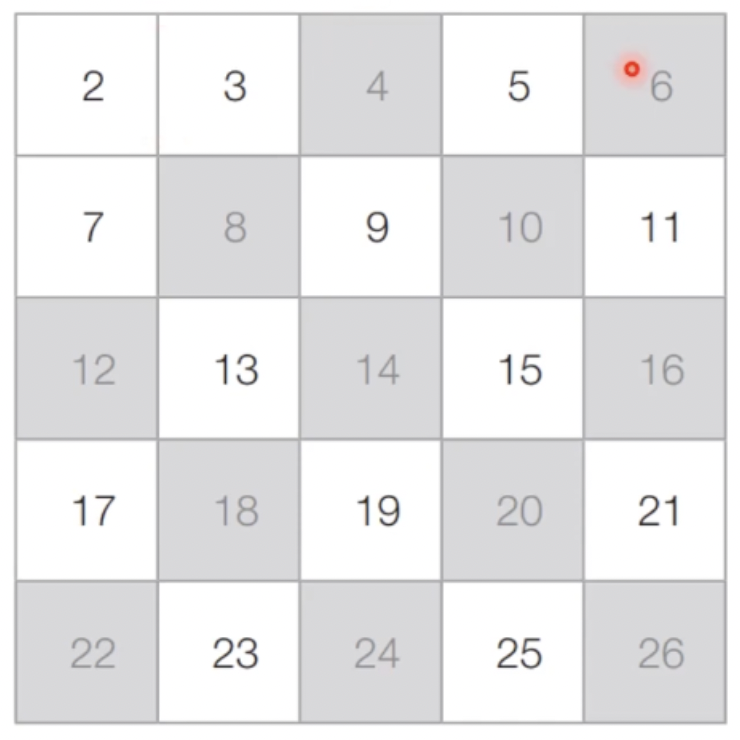
  • [Step 2] 아직 처리하지 않은 가장 작은 수 3을 제외한 3의 배수 모두 제거
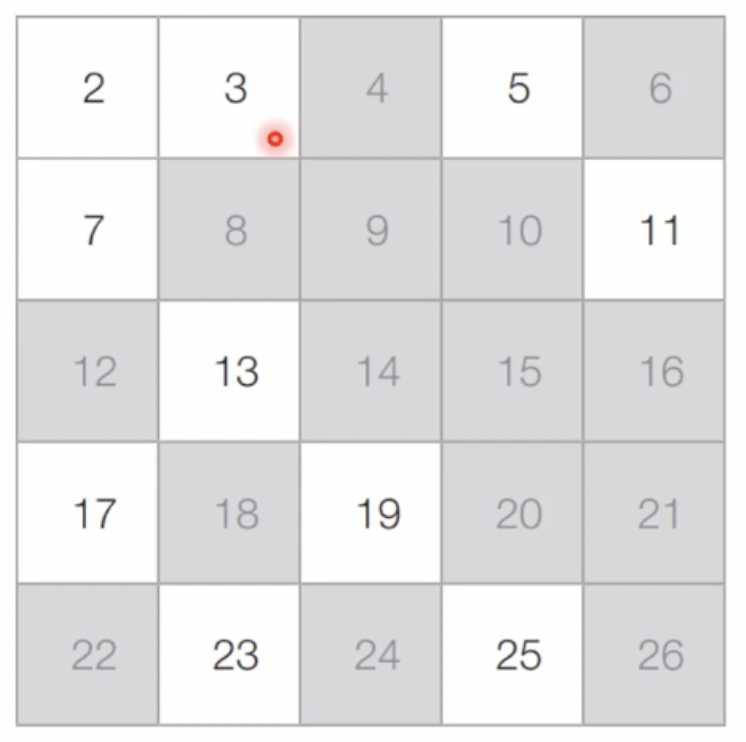
  • [Step 3] 아직 처리하지 않은 가장 작은 수 5를 제외한 5의 배수 모두 제거
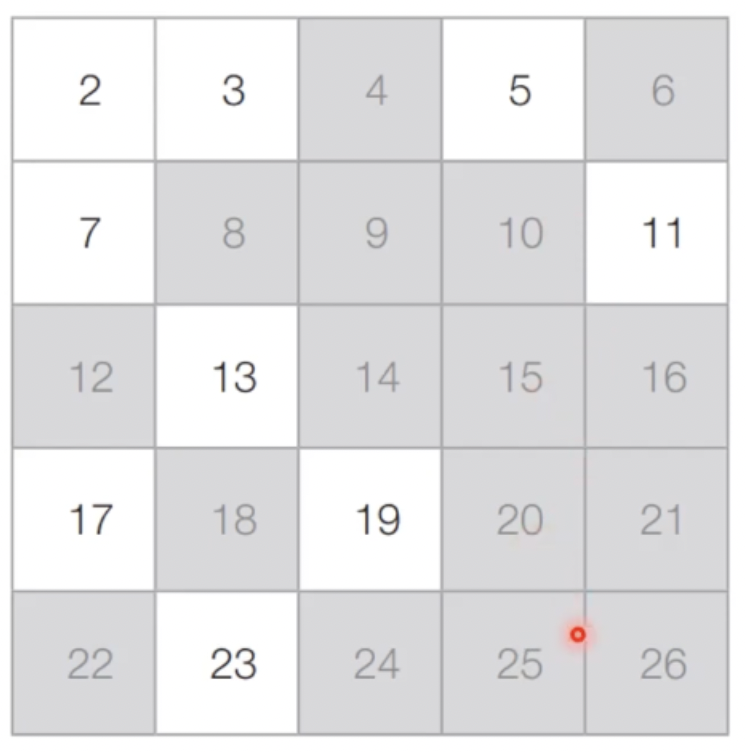
  • [Step 4] 마찬가지의 과정을 반복했을 때의 최종적인 결과

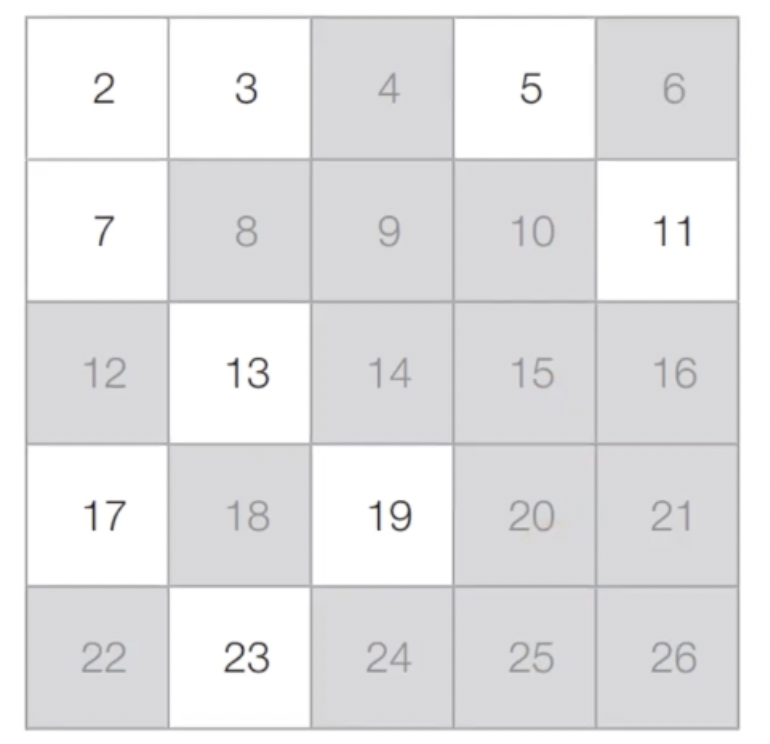
• 코드

  import math
  
  n = 1000 # 2부터 1,000까지의 모든 수에 대하여 소수 판별
  array = [True for i in range(n + 1)] # 처음엔 모든 수가 소수(True)인 것으로 초기화
  
  # 에라토스테네스의 체 알고리즘 
  for i in range(2, int(math.sqrt(n)) + 1): # 2부터 n의 제곱근까지의 모든 수를 확인하며
      if array[i] == True: # i가 소수인 경우 (남은 수인 경우)
          # i를 제외한 i의 모든 배수를 지우기
          j = 2 
          while i * j <= n:
              array[i * j] = False
              j += 1
  
  # 모든 소수 출력
  for i in range(2, n + 1):
      if array[i]:
          print(i, end=' ')

• 에라토스테네스의 체의 시간복잡도

  • 사실상 선형시간에 가까울정도로 매우 빠름
  • 시간복잡도는 O(NloglogN)
  • 다수의 소수를 찾아야하는 문제에서 효과적으로 사용될 수 있지만 각 자연수에 대한 소수 여부를 저장해야하므로 메모리가 많이 필요함
  • 10억이 소수인지 아닌지 판별해야 할 때 사용하긴 힘듦

참고: 이것이 취업을 위한 코딩 테스트다 with 파이썬 (취업과 이직을 결정하는 알고리즘 인터뷰 완벽 가이드), 유튜브 강의 영상