[코딩 테스트] - 최단 경로 알고리즘 문제 풀이

Jeonghwan Kim·2022년 11월 8일

최단 경로 알고리즘 코딩테스트

코딩 테스트

목록 보기

13/21

최단 경로 알고리즘 문제 풀이

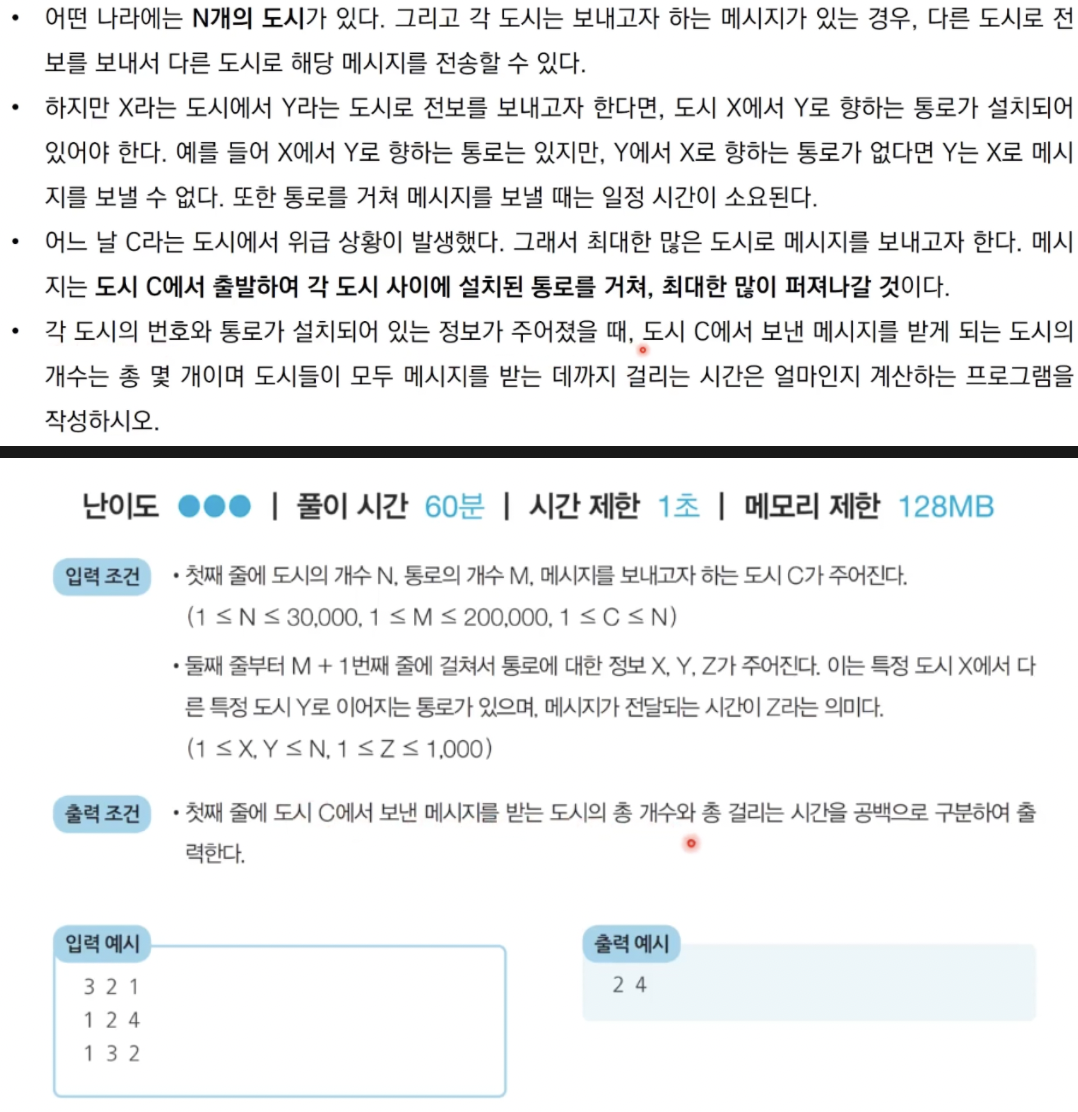
<문제> 전보

문제 해결 아이디어
- 한 도시에서 다른 도시까지의 최단 거리 문제로 치환
- N과 M의 범위가 충분히 크기 때문에 우선순위 큐를 활용한 다익스트라 알고리즘을 구현함

코드

import heapq
import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수, 간선의 개수, 시작 노드를 입력받기
n, m, start = map(int, input().split())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)

# 모든 간선 정보를 입력받기
for _ in range(m):
    x, y, z = map(int, input().split())
    # X번 노드에서 Y번 노드로 가는 비용이 Z라는 의미
    graph[x].append((y, z))

def dijkstra(start):
   q = []
   # 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
   heapq.heappush(q, (0, start))
   distance[start] = 0
   while q: # 큐가 비어있지 않다면
        # 가장 최단 거리가 짧은 노드에 대한 정보를 꺼내기
        dist, now = heapq.heappop(q)
        if distance[now] < dist:
            continue
        # 현재 노드와 연결된 다른 인접한 노드들을 확인
        for i in graph[now]:
            cost = dist + i[1]
            # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(q, (cost, i[0]))

# 다익스트라 알고리즘을 수행
dijkstra(start)

# 도달할 수 있는 노드의 개수
count = 0
# 도달할 수 있는 노드 중에서, 가장 멀리 있는 노드와의 최단 거리
max_distance = 0
for d in distance:
    # 도달할 수 있는 노드인 경우
    if d != 1e9:
        count += 1
        max_distance = max(max_distance, d)

# 시작 노드는 제외해야 하므로 count - 1을 출력
print(count - 1, max_distance)

<문제> 미래도시

문제 해결 아이디어
- 전형적인 최단 거리 문제이므로 최단 거리 알고리즘을 이용해 해결함
- N의 크기가 최대 100이므로 플로이드 워셜 알고리즘을 이용해도 효율적으로 해결할 수 있음
- 플로이드 워셜 알고리즘을 수행한 뒤에 (1번 노드에서 X까지의 최단거리 + X에서 K까지의 최단 거리)를 계산하여 출력하면 정답임
- 각 간선은 양방향 간선이며, 간선의 비용은 모두 1임

코드

INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수 및 간선의 개수를 입력받기
n, m = map(int, input().split())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]

# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
    for b in range(1, n + 1):
        if a == b:
            graph[a][b] = 0

# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
    # A와 B가 서로에게 가는 비용은 1이라고 설정
    a, b = map(int, input().split())
    graph[a][b] = 1
    graph[b][a] = 1

# 거쳐 갈 노드 X와 최종 목적지 노드 K를 입력받기
x, k = map(int, input().split())

# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
    for a in range(1, n + 1):
        for b in range(1, n + 1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

# 수행된 결과를 출력
distance = graph[1][k] + graph[k][x]

# 도달할 수 없는 경우, -1을 출력
if distance >= 1e9:
    print("-1")
# 도달할 수 있다면, 최단 거리를 출력
else:
    print(distance)