밑바닥부터 시작하는 딥러닝 #3-3 손실함수, 미분, 기울기
Prologue
나는 여전히 웹개발자이지만, 회사에 부쩍 딥러닝 과제가 많아져서 딥러닝 공부가 많이 필요하게 됐다. 밑바닥부터 시작하는 딥러닝 책이 좋다고 해서 천천히 하나하나 공부해보려 한다.
손실함수의 사용 이유
최적의 가중치와 편향을 탐색할 때 손실함수의 값을 가능한 한 작게 하는 매개변수의 값을 찾습니다. 이 때 매개변수의 미분을 계산하고 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복합니다.
손실함수의 미분이란 '가중치 매개변수의 값을 아주 조금 변화시켰을 때, 손실함수가 어떻게 변하는지'입니다.
그렇다면, 왜 직접적인 '정확도'라는 지표를 놔두고 '손실함수의 값'이라는 지표를 사용할까요? 정확도를 지표로 삼으면 미분 값이 대부분의 장소에서 0이 되어 매개변수를 갱신할 수 없기 때문입니다.
신경망을 학습할 때, 정확도를 지표로 삼으면 매개변수의 미분이 대부분의 장소에서 0이 됩니다.
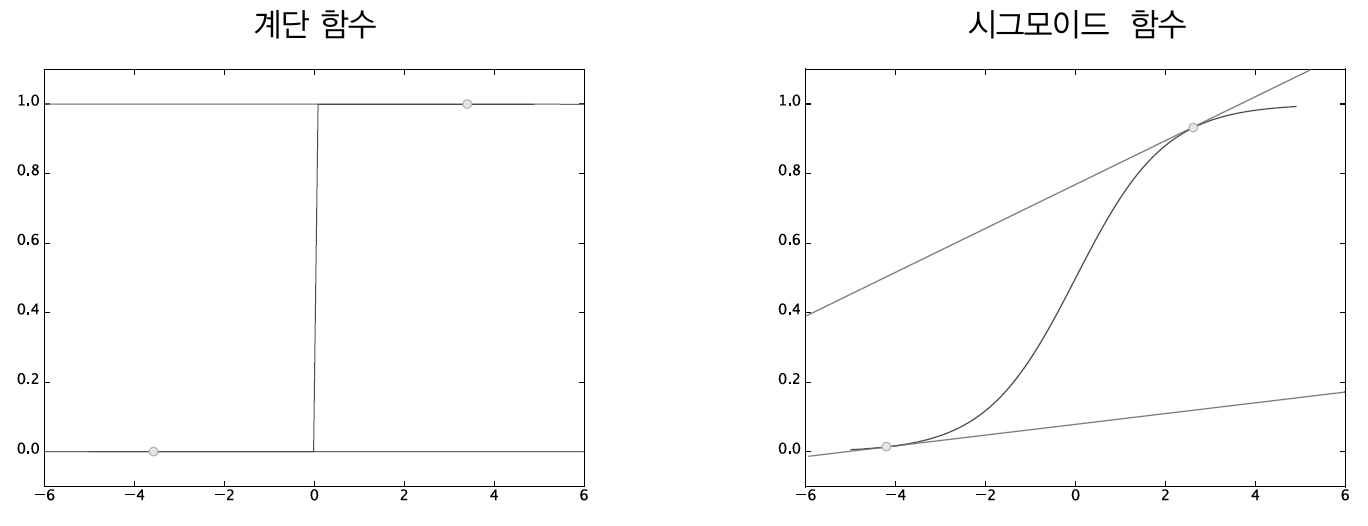
정확도는 매개변수의 미세한 변화에는 반응을 보이지 않고, 반응이 있더라도 그 값이 불연속적으로 갑자기 변화합니다. 계단함수와 비슷하게 생각하면 됩니다. 계단함수는 대부분의 장소에서 미분 값이 0입니다.
반면 시그모이드 함수는 출력이 연속적으로 변하고 곡선의 기울기도 연속적으로 변합니다. 시그모이드 함수의 미분은 어느 장소라도 0이 되지는 않습니다. 이처럼 기울기가 0이 되지 않는 덕분에 신경망이 올바르게 학습할 수 있는 것입니다.
미분
미분은 특정 순간의 변화량을 말합니다.
수식
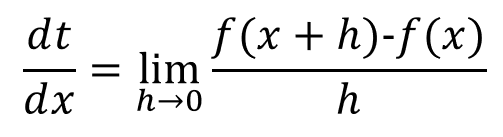
코드

위는 미분을 코드로 구현한 나쁜 예입니다. h를 0으로 수렴하게 하고 싶어서, 최대한 작은 값을 넣었지만 저렇게 작은 값을 넣으면 반올림 오차 라는 문제를 일으킵니다.
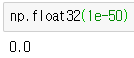
위와 같이 최종 계산 결과에 오차가 생겨 0.0으로 표기됩니다. 그래서 약 1e-4정도의 값이 적당합니다. 일반적으로 그정도면 좋은 결과를 얻는다고 여겨집니다.
위에서 h를 약 1e-4정도의 값으로 한다고 했는데 이렇게 되면 사실 오차가 발생합니다. 이러한 오차를 줄이기 위해 (x + h)와 (x - h)일 때의 함수 f의 차분을 계산하는 방법을 쓰기도 합니다.
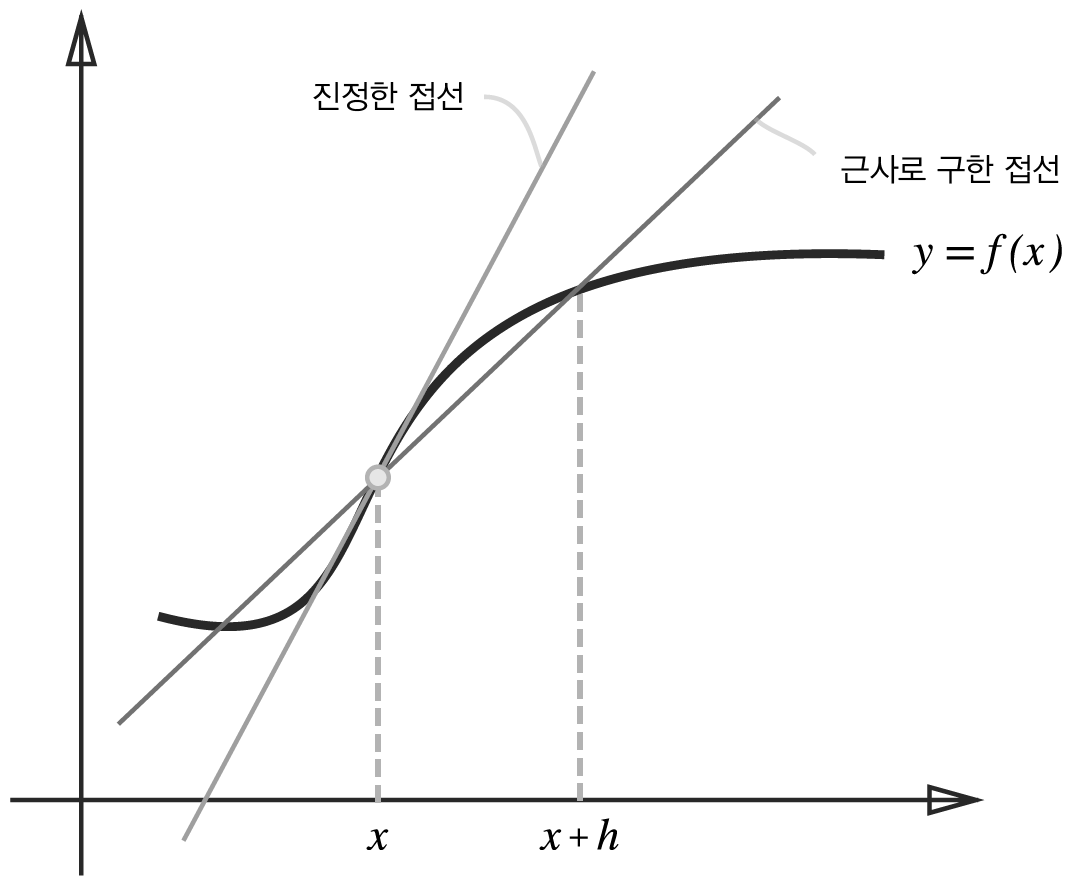
여기서 h를 0에 수렴하게 하는 것이 사실상 불가능하기 때문에 우리가 구한 접선과 진정한 접선이 다릅니다.
기존의 방법은 x와 x+h의 기울기를 구하는 전방 차분 이었다면, 새로운 방법은 x-h, x, x+h의 차분을 계산하는 중심차분 혹은 중앙차분 이라고 불리는 방법을 사용합니다.

아주 작은 차분으로 미분하는 것을 수치 미분 이라 합니다. 수식을 전개하여 오차를 포함하지 않는 미분은 해석적 미분 이라 합니다.
수치미분 사용해보기
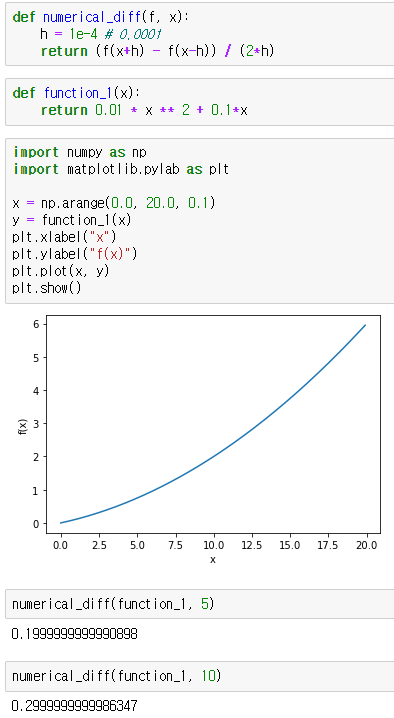
위의 코드는 앞서 만든 코드를 실제로 사용해본 결과입니다. 해석적 미분 결과(0.20, 0.30)와 비교했을 때 매우 적은 오차를 보이고 있습니다.
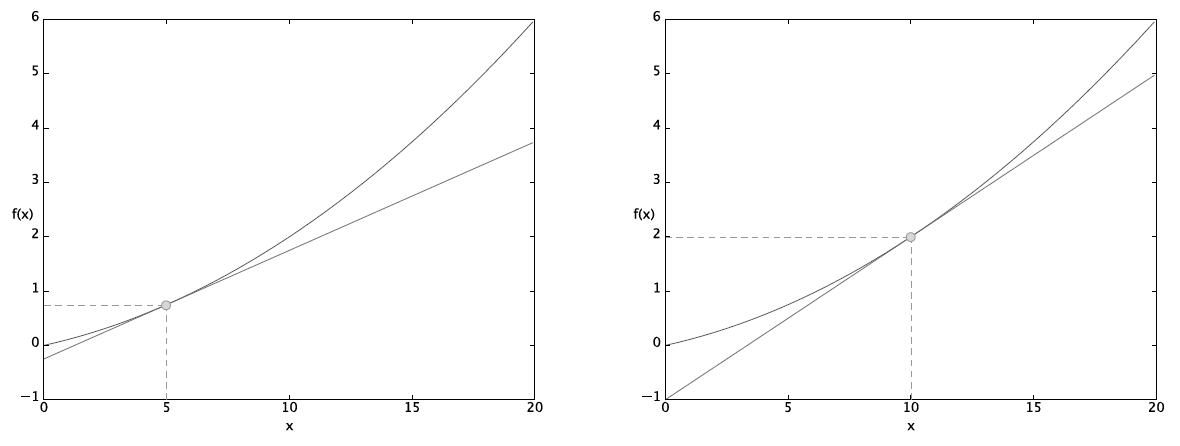
아래는 접선을 시각화한 것입니다. 각각 x는 5일 때와 10일 때입니다.
편미분 사용해보기
변수가 여럿인 함수에 대한 미분을 편미분 이라 합니다. 편미분은 미분할 변수 하나를 제외한 뒤, 나머지를 고정 값으로 둔 채 문제를 풀면 됩니다.
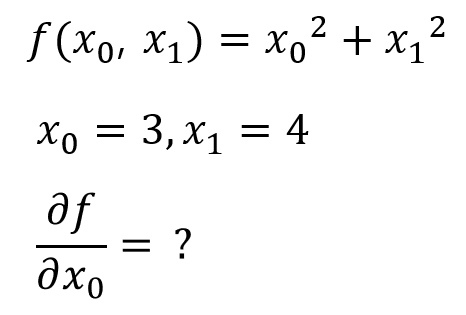
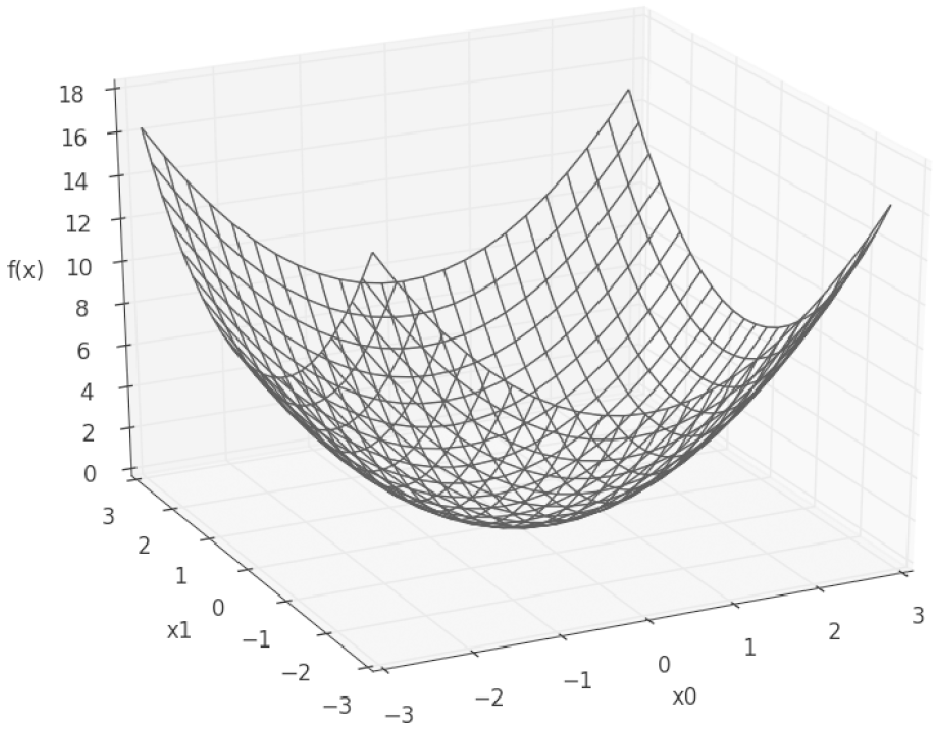
위의 함수를 그래프로 그리면 아래와 같은 그림이 나옵니다.
위의 문제를 코드로 풀면 아래의 코드가 나옵니다.
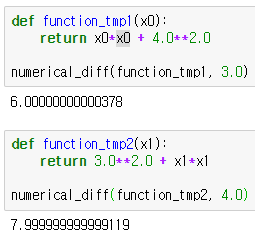
해석적 미분과 거의 동일한 값이 나옵니다.
기울기(gradient)
위에선 변수가 여러개일 때 하나씩 미분하는 편미분을 배워봤습니다. 그렇다면 여러 개의 편미분을 동시에 계산하고 싶다면 어떻게 해야 할까요?
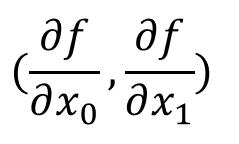
위와 같은 형식으로 모든 편미분을 벡터 형식으로 정리한 것을 기울기(gradient) 라고 합니다.

위는 기울기를 계산하는 코드입니다.
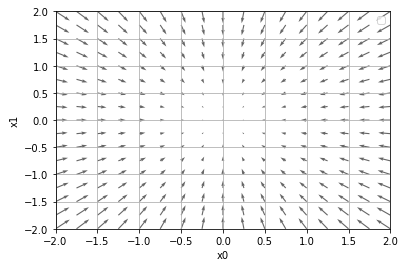
위는 기울기 벡터의 방향을 시각화한 것입니다. 기울기는 각 지점에서 기울기가 낮아지는 지점을 가리킵니다. 기울기가 가리키는 쪽은 각 장소에서 손실 함수의 출력 값을 가장 크게 줄이는 방향 입니다.
정리
- 신경망을 학습할 때 지표는 정확도가 아닌 손실함수를 사용합니다. (정확도를 지표로 삼으면 매개변수의 미분이 대부분의 장소에서 0이 됩니다.)
- 학습을 위해 미분을 할 때는 기존 수학적 개념인 '해석학적 미분' 이 아닌 '수치 미분' 을 하게 됩니다. 이 때 h의 값은 1e-4 정도를 사용하면 결과가 괜찮습니다. 너무 작은 값을 사용하면 오차가 심해집니다.
- 오차를 줄이기 위해 중앙차분미분 ((f+h)-(f-h)/2h) 을 합니다.
- 편미분은 미분할 값을 제외한 나머지 값을 고정하고 미분을 진행하면 됩니다.
- 편미분한 값들을 벡터 형식으로 모아두면 기울기 가 됩니다.
- 기울기가 가리키는 쪽은 각 장소에서 손실 함수의 출력 값을 가장 크게 줄이는 방향 입니다.
