자바스크립트로 알고리즘 정리하기 #9 다이나믹 프로그래밍 개념

자바스크립트로 알고리즘 정리하기 #9 다이나믹 프로그래밍 개념

다이나믹 프로그래밍 개념

• 큰 문제를 작은 문제로 나눠서 푸는 알고리즘이다.
  • 분할정복(Divide and Conquer)도 큰 문제를 작은 문제로 나눠서 푸는 알고리즘이다.
  • 다이나믹 프로그래밍과 분할 정복의 차이는 큰 문제를 작은 문제로 나눴을 때, 중복이 가능한지 불가능한지이다.
    • 다이나믹 프로그래밍은 작은 문제의 중복이 된다.
    • 분할정복은 작은 문제의 중복이 안 된다.
  • 10을 나눌 때 분할정복이라면 5/5, 6/4, 7/3, 3/7과 같이 중복이 되지 않게 나눈다.
  • 10을 나눌 때 다이나믹 프로그래밍이라면 5, 5, 3과 같이 중복이 되게 나눈다.
• 다이나믹 프로그래밍이란 이름 자체에는 아무런 의미가 없다.

다이나믹 프로그래밍으로 풀 수 있는 문제의 속성

1. 겹치는 부분 문제가 있는 경우 (Overlapping Subproblem)

• 큰 문제를 작은 문제로 쪼갤 수 있는 경우

2. 최적화 부분 구조 (Optimal Substructure)

• 작은 문제를 풀어나감으로써 큰 문제의 정답을 구할 수 있는 경우

겹치는 부분 문제가 있는 경우 (Overlapping Subproblem)

피보나치 수열

• F0 = 0
• F1 = 1
• Fn = Fn-1 + Fn-2 (n >= 2)

피보나치 수열의 큰 문제를 작은 문제로 나누기

• 큰 문제 : N번째 피보나치 수를 구하는 문제

• 작은 문제 : N-1번째 피보나치 수를 구하는 문제, N-2번째 피보나치 수를 구하는 문제

• 큰 문제2 : N-1번째 피보나치 수를 구하는 문제

• 작은 문제2 : N-2번째 피보나치 수를 구하는 문제, N-3번째 피보나치 수를 구하는 문제

• 큰 문제3 : N-2번째 피보나치 수를 구하는 문제

• 작은 문제3 : N-3번째 피보나치 수를 구하는 문제, N-4번째 피보나치 수를 구하는 문제

주로 이러한 경우에는 재귀를 사용한다.

최적화 부분 구조 (Optimal Substructure)

문제의 정답을 작은 문제의 정답에서 구할 수 있는 경우

• 서울에서 부산을 가는 가장 빠른 길이 대전과 대구를 순서대로 거쳐야 한다면,
  • 서울 -> 대전 -> 대구 -> 부산
• 대전에서 부산을 가는 가장 빠른 길은? 대구를 거쳐야 한다.
  • 만일 대전에서 부산을 가는 가장 빠른 길이 울산을 거쳐야 한다면?
  • 서울 -> 대전 -> 울산 -> 부산이 되는 것이 맞다.
  • 작은 문제의 정답을 이용하여 큰 문제의 정답을 구할 수 있음

피보나치 수열의 경우

• Optimal Substructure를 만족하면, 문제의 크기에 상관 없이 어떤 한 문제의 정답이 일정하다.
• 몇번째 피보나치 수를 구하든지에 상관없이 n번째 피보나치수는 항상 동일하다.

다이나믹 프로그래밍 최적화의 핵심

• 각 작은 문제는 한 번만 풀어야 한다.
• Optimal Substructure를 만족하기 때문에, 같은 문제는 구할 때마다 정답이 같다.
• 정답을 한 번 구했으면, 어딘가에 메모해놓는다.
• 메모하는 것을 코드에서는 배열로 구현할 수 있다.
• 메모한다고 해서 Memoization 이라는 용어를 쓴다.

dp를 이용해 피보나치 수 구현해보기

let fibo = (n) => (n > 2 ? fibo(n - 2) + fibo(n - 1) : 1);

위는 일반적으로 재귀를 이용하는 피보나치 수 구현이다.

n = 1, 2일 때 초기값 1을 부여해주고 2를 넘는 값이 들어올 때부터는 n-1 n-2 위치에 있는 값을 합한 것이 n이 되는 방식이다.

예로 5번째 피보나치 수를 구할 때 재귀를 이용하면

5번째의 피보나치 수를 구하기 위해
4번째 3번째의 피보나치 수를 구해야 하고

5번째 내부 4번째의 피보나치 수를 구하기 위해
3번째 2번째의 피보나치 수를 구해야 하고
3번째 피보나치 수를 구하기 위해
2번째 1번째의 피보나치 수를 구해야 한다.

5번째 내부 3번째의 피보나치 수를 구하기 위해
3번째 2번째의 피보나치 수를 구해야 하고
3번째 피보나치 수를 구하기 위해
2번째 1번째의 피보나치 수를 구해야 한다.

5번째의 피보나치 수를 구하는데 위와 같은 과정을 거쳐야 한다.
계속 같은 번째 피보나치 수를 구하는 과정을 반복해야 한다.

사실 이미 계산했던 값을 이용하면 되는 것이라 위와 같은 방법으로 구현하면 매우 비효율적이다.

그래서 아래의 방법을 이용할 수 있다.

let fiboArr = [0];
let fiboWithMemoization = (n) => {
  if (n < 3) {
    fiboArr[n] = 1;
  }

  if (!fiboArr[n]) { // 내가 저장한 값 중에 없다면 ...
    // 재귀를 이용해 구하고 저장
    fiboArr[n] = fiboWithMemoization(n - 1) + fiboWithMemoization(n - 2);
  }

  return fiboArr[n];
};

위는 dp를 이용한 피보나치 수 구현이다. fiboArr이라는 곳에 내가 계산해둔 피보나치 수를 저장해둔다. 이러한 방식의 차이는 속도면에서 어마어마한 차이를 가져온다.

이를테면 50번째 피보나치 수를 구하는 것은 메모이제이션을 사용하지 않은 단순 재귀에서는 어마어마한 시간이 걸리지만, 메모이제이션을 사용한 피보나치 수 구하기 함수를 이용하면 금방 나온다.

시간복잡도 비교

메모이제이션 없는 재귀함수의 총 함수 호출 횟수

• n=0일 때
  • 계산 없음, 1 반환
  • 계산 1회
• n=1일 때
  • 계산 없음, 1 반환
  • 계산 1회
• n=2일 때
  • n=0일 때 계산 1회
  • n=1일 때 계산 1회
  • n=0일 때와 n=1일 때를 더해주는 연산 1회
  • 총 3회
• n=3일 때
  • n=2일 때 3회
  • n=1일 때 1회
  • n=2일 때와 n=1일 때를 더해주는 연산 1회
  • 총 5회
• n=4일 때
  • n=3일 때 5회
  • n=2일 때 3회
  • n=3일 때와 n=2일 때를 더해주는 연산 1회
  • 총 9회
• n=5일 때
  • n=4일 때 9회
  • n=3일 때 5회
  • n=4일 때와 n=3일 때를 더해주는 연산 1회
  • 총 15회

위와 같은 횟수의 연산을 계속한다.

계속 n-1의 연산횟수 + n-2의 연산횟수 + 1회 가 추가된다.

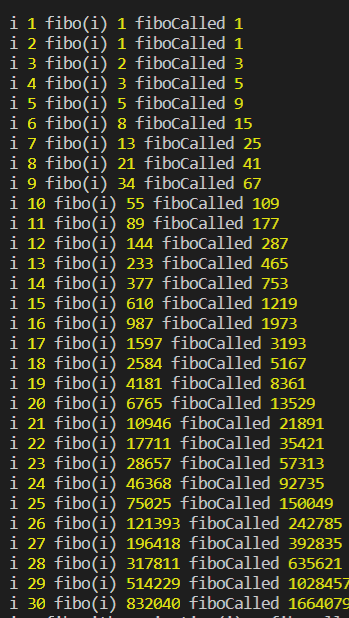
30번째 피보나치 수를 구하는데까지 드는 연산횟수를 프로그램으로 측정해보았다.

총 함수호출이 4356586번만큼 이루어진다.

메모이제이션 있는 재귀함수

• n=0일 때
  • 1 반환
  • n[0] = 1
  • 1회
• n=1일 때
  • 1 반환
  • n[1] = 1
  • 1회
• n=2일 때
  • n[2] = n[0] + n[1]
  • n[0]일 때 1회 + n[1]일 때 1회 + 둘을 더하는 1회
• n=3일 때
  • n[3] = n[1] + n[2]
  • n[1]일 때 1회 + n[2]일 때 1회 + 둘을 더하는 1회
    ...

위와 같은 숫자로 계산하게 된다. n이 몇이든 계속 3회의 함수호출만 추가된다.

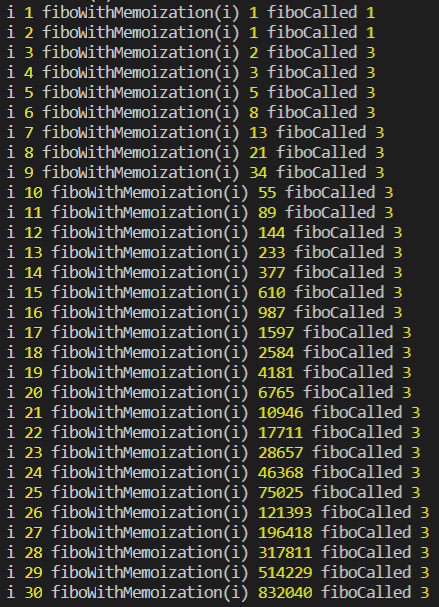
총 함수호출이 86번만큼 이루어진다.

결론

메모이제이션을 하지 않으면, O(대략 피보나치 n번째까지의 총합)만큼의 시간에 값을 구하게 된다. 대략 O(2n제곱) 만큼의 시간복잡도가 걸린다.

메모이제이션을 하면 대략 O(3n)만큼의 시간에 값을 구하게 된다.

다이나믹 프로그래밍의 구현 방식

1. Top-down

• 큰 문제부터 문제를 쪼개가며 작은 문제로 만들고 다시 합쳐가며 원래 문제를 푸는 방식

2. Bottom-up

• 작은 문제들을 모아서 큰 문제를 만들어 쌓아 올려가는 방식

앞에 서봤던 재귀 방식은 Top-down 방식이라고 할 수 있음

Bottom-up은 주로 반복문을 사용해서 구현함

// bottom-up의 예제
int d[100];
int fibonacci(int n) {
  d[0] = 0;
  d[1] = 1;
  
  for(int i=2; i<=n; i++){
    d[i] = d[i-1] + d[i-2];
  }
  
  return d[n];
}

사실 두 방법 중 하나만 알아도 다이나믹프로그래밍 문제를 푸는데는 큰 지장이 없다.

Top-down과 Bottom-up의 시간차이는?

알 수 없다. 일단은 재귀는 함수 호출 과정이 많이 들어가서 스택 오버플로우를 만들 수도 있고, 반복문이 더 빠를 것 같은데 알 수 없는 이유는 Bottom-up 방식은 정말 모든 문제를 풀고 Top-down은 그렇지 않은 경우가 있기 때문에 알 수 없다.

재귀로 풀었을 때 Stack Overflow가 났다면 다이나믹 프로그래밍을 잘못 구현했을 확률이 높다.

Python 언어를 사용하는 경우에는 스택오버플로 현상 때문에 Top-down보다는 Bottom-up이 유리하다. C, Java 등의 언어에는 상관없다.

Top-down과 Bottom-up은 서로 대체 가능한가?

대체 가능하다. 대부분 Top-down으로 풀 수 있는 문제는 Bottom-up으로도 풀 수 있다.

다이나믹 프로그래밍 문제풀이 전략

1. 점화식의 정의를 세운다.
2. 실제 점화식을 만든다.

조금 어려워지면 점화식의 정의를 조금 변경해야 하는 어려운 문제들이 나온다.