Algorithm Study #6 (Graph_Expression_How_To_Save_Graph)

Representation of Graph

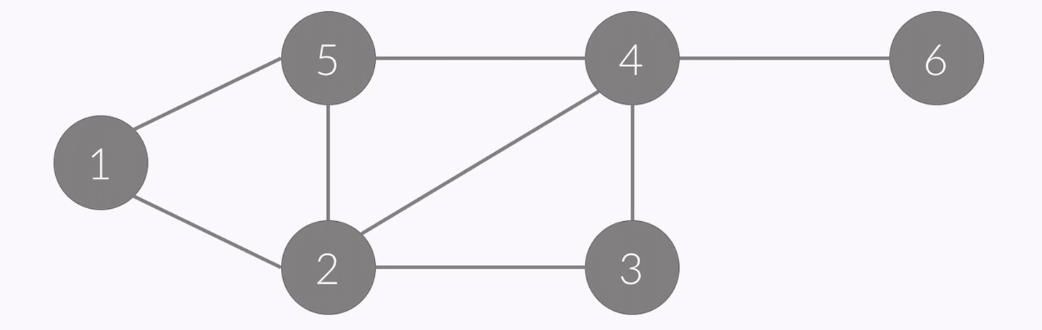
• in case of this graph, it has 6 vertices and 8 edges
• it doesn't have direction so it is undirected graph
• vertices : {1, 2, 3, 4, 5, 6}
• edges : {(1, 2), (1, 5), (2, 5), (2, 3), (3, 4), (2, 4), (4, 5), (4, 6)}
• vertices are usually named just 1 to the amount of vertices
  - so edges are important
  • we only save the amount of vertices by using variable.
• if we just want to express graph, it is the same to just save the all of edges.
  - edge can save effectively
  - we can figure out the graph's representation

Adjacency Matrix (Without Weight)

• When you say the number of vertices is V
  - We use 2 dimension array which has size of V * V
• A[i][j] = 1 (when there is edge connecting i to j), 0 (no edge)
• in case of graph at the top, it can be expressed like this

/ 1 2 3 4 5 6
1 0 0 0 0 1 0
2 1 0 1 1 1 0
3 0 1 0 1 0 0
4 0 1 1 0 1 1
5 1 1 0 1 0 0
6 0 0 0 1 0 0

• These numbers are symmetrical in relation of the diagonal
• it has dis-advantage
  - it saves useless edges
  - even if it doesn't have any edge, it saves 0 in that space
• usually, V^2 >= E
• to solve easy problems, it is good way to express graph data structure.

  	```c++
  	#include <cstdio>
  	#include <vector>
  	int a[10][10];
  	int main() {
  int n, m;
  scanf("%d %d", &n, &m);
  for (int i=0; i<m; i++){
    int u, v;
    scanf("%d %d", &u, &v);
    a[u][v] = a[v][u] = 1; // it means undirected graph
  }

  }

  	```

Adjacency Matrix (With Weight)

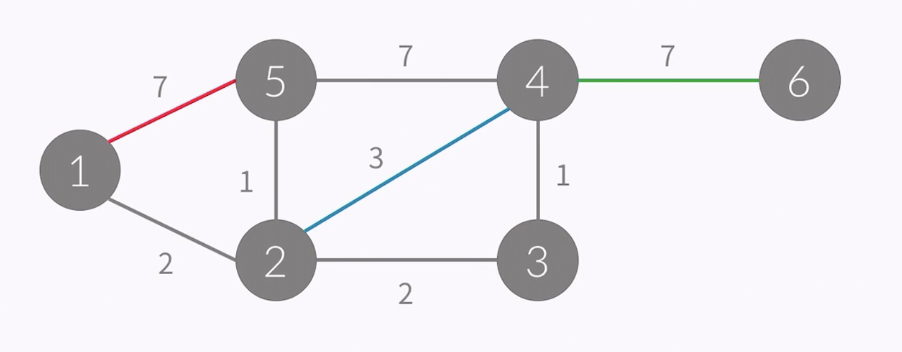
• it is similar to that of undirected grpah
• but when it is saved it doesn't just save 1 but its weight
• A[i][j] = w (there is edge connecting from i to j), 0 (no edge)
• if range of w is -9999 <= w <= 9999, we can make 2 arrays.
  - one expresses edges connecting vertices
  • another expresses weight of edges
    - graph above can be expressed like this.

/ 1 2 3 4 5 6
1 0 2 0 0 7 0
2 2 0 2 3 1 0
3 0 2 0 1 0 0
4 0 3 1 0 7 7
5 7 1 0 7 0 0
6 0 0 0 7 0 0

• code

#include <cstdio>
#include <vector>
int a[10][10];
int main() {
  int n, m;
  scanf("%d %d", &n, &m);
  for (int i=0; i<m; i++){
    int u, v;
    scanf("%d %d", &u, &v);
    a[u][v] = a[v][u] = 1; // it means undirected graph
  }
}

Adjacency List (Without Weight)

• implement using linked-list
• in A[i], there are linked lists which is connected with 'i'
  
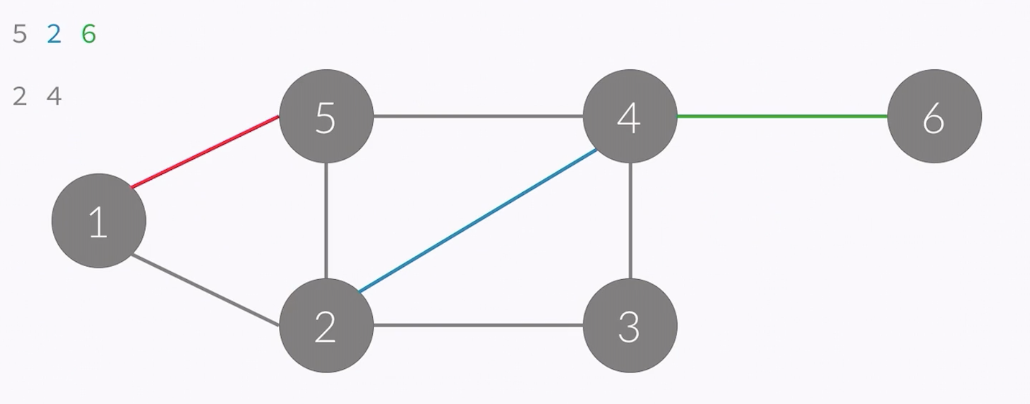
• in this case,
  - A[1]: 2 5
  • A[2]: 1 3 4 5
  • A[3]: 2 4
  • A[4]: 3 5 2 6
  • A[5]: 1 2 4
  • A[6]: 4
    • the numbers in array actually doesn't mean vertex but edges
      - the amount of its numbers means 'degree'
• it needs space of O(E)
• since LinkedList takes too much time to implement, it is usually implemented with vector in which length can be changed
• it is used to use space only needed

#include <cstdio>
#include <vector>
using namespace std;
vector<int> a[10]; // it is different from expression like a(10)
				   // a[10] means 10 of 2 dimension array which has changable size
int main() {
  int n, m;
  scanf("%d %d", &n, &m);
  for (int i=0; i<m; i++) {
    int u, v;
    scanf("%d %d", &u, &v);
    a[u].push_back(v); // it means undirected graph
    a[v].push_back(u);
  }
}

Adjacency List (With weight)

• it saves edges and weight like below
  - A[1]: (2, 2) (5, 7)
  • A[2]: (1, 2) (3, 2) (4, 3) (5, 1)
  • A[3]: (2, 2) (4, 1)
  • A[4]: (3, 1) (5, 7) (2, 3) (6, 7)
  • A[5]: (1, 7) (2, 1) (4, 7)
  • A[6]: (4, 7)
• implementation

#include <cstdio>
#include <vector>
using namespace std;
vector<pair<int, int>> a[10];
int main() {
  int n, m;
  scanf("%d %d", &n, &m);
  for (int i=0; i<m; i++) {
    int u, v, w;
    scanf("%d %d %d", &u, &v, &w);
    a[u].push_back(make_pair(v, w));
    a[v].push_back(make_pair(u, w));
  }
}

Space Complexity of Adjacency Matrix and List

• Adjacency Matrix : O(V^2)
• Adjacency List : O(E)
  - in most cases, we don't need much space for edges
  • so adjacency list is usually right choice to use

Edge-list

• it is implemented by using array
• it saves all of edges
• for example)
  - E[0] = 1 2
  • E[1] = 1 5
  • E[2] = 2 3
  • ....
    • each means start point of edge and end point of edge
• if there are 8 edges and the graph is undirected, to implement this, we need 16 spaces
• it should be sorted start point of edge first
• after sorting there should be array like this.
  - i .... 0 1 2 3 4 5 6
  • cnt[i] 0 2 4 2 4 3 1
  • it means the number of edges in the graph
• implementation

for (int i=0; i<m; i++) {
  cnt[e[i][0]] += 1;
}

• after getting the number of all edges to N
• accumulate like this again
  - i .... 0 1 2 3 4 5 6
  • cnt[i] 0 2 6 8 12 15 16
• implementation

for (int i=1; i<=n; i++) {
  cnt[i] = cnt[i-1] + cnt[i];
}

• after this, amazing thing happens
  - the range from cnt[i-1] to cnt[i]-1 means that E[cnt[i-1] to E[cnt[i]-1] is the range of the edge number i
  - for example)
  - edges of vertex 1 exists from E[0] to E[1]
  - 0 = cnt[i-1], 1 = cnt[i]-1

meaning of Saving Graph

• it means we want to save edges
• there are three ways
  - adjacency matrix
  - ineffective
  • adjacency list
  • edge list