Algorithm Study #6 (Graph Search)

Search of Graph

• There are two kinds of way to search graph
  - DFS and BFS
  - DFS
  - Depth First Search Algorithm
  - Search graph as deeply and many as it can
  - It uses Stack
  - BFS
  - Breadth First Search Algorithm
  - Search graph as broadly as it can
  - It uses Queue
  - When all edges' weight is 1
  - it becomes the algorithm for getting shortest distance
• Purpose of graph search (DFS, BFS)
  - To visit all vertices once
• Algorithm of DFS
  - by using stack, it goes as much as it can
  • when there is no way to go, it goes back to a previous vertex
    - example)
    • first, to check if this vertex is already visited
      • it's good to make array for remembering the vertex number it visited.
        - i ........... 1 2 3 4 5 6
        • check[i] 1 0 0 0 0 0
          • it is a first state. start point is 1 and it is not moving yet
            • when all of check array's value have value of 1, this algorithm will be over.
              
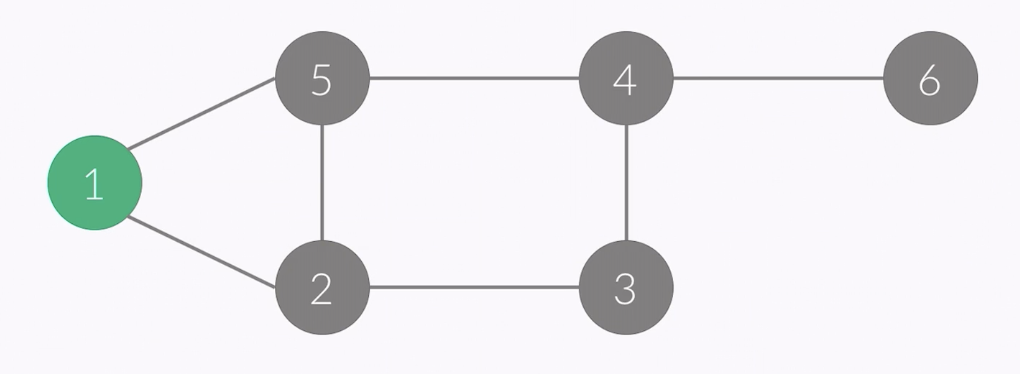
              - when graph's state is like this, it can move any direction (2 or 5).
              - but in this case, we will make this go to smaller number first.
              
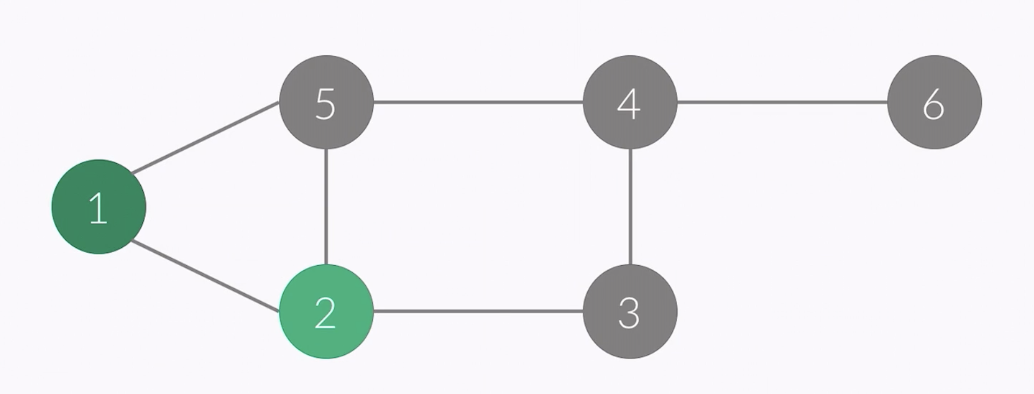
              - so it went to number 2
        • and array will be like
          - i ........... 1 2 3 4 5 6
          - check[i] 1 1 0 0 0 0
          - vertex of this point : 2
        • order : 1 2
        • stack : 1 2
          
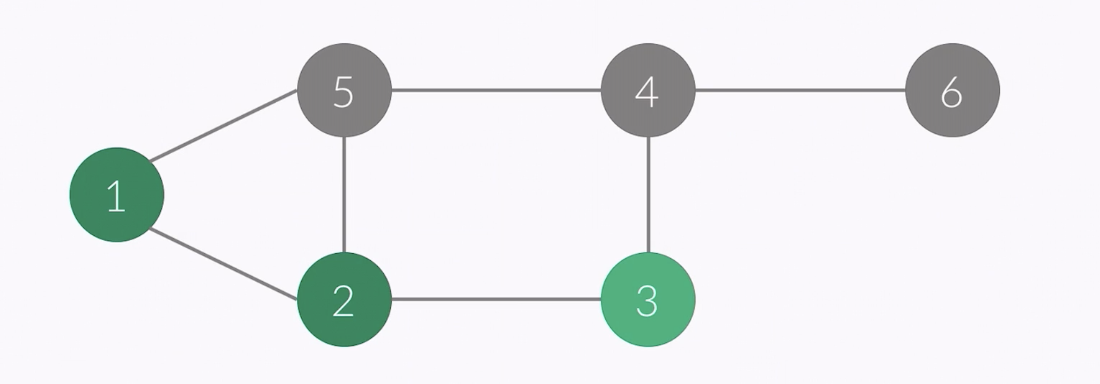
          - vertex of this point : 3
          - i ........... 1 2 3 4 5 6
          - check[i] 1 1 1 0 0 0
        • order : 1 2 3
        • stack : 1 2 3
          
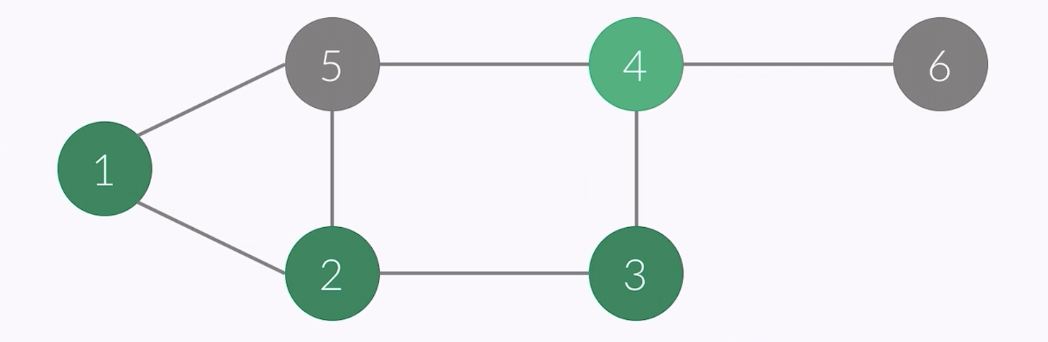
          - vertex of this point : 4
          - i ........... 1 2 3 4 5 6
          - check[i] 1 1 1 1 0 0
        • order : 1 2 3 4
        • stack : 1 2 3 4
          
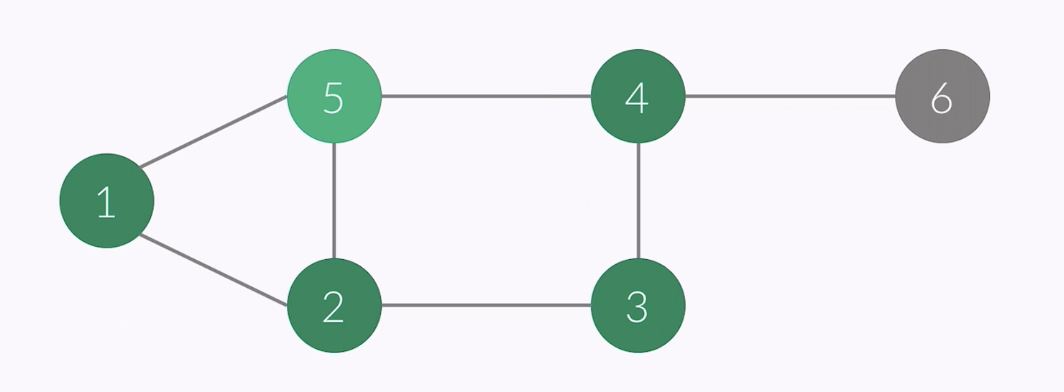
          - vertex of this point : 5
          - i ........... 1 2 3 4 5 6
          - check[i] 1 1 1 1 1 0
        • order : 1 2 3 4 5
        • stack : 1 2 3 4 5
        • in this case, it has to go back to go to vertex 6
          • by using stack, it can trace the number of vertices it has stopped by at
            • after popping stack it will go to vertex number 4
              
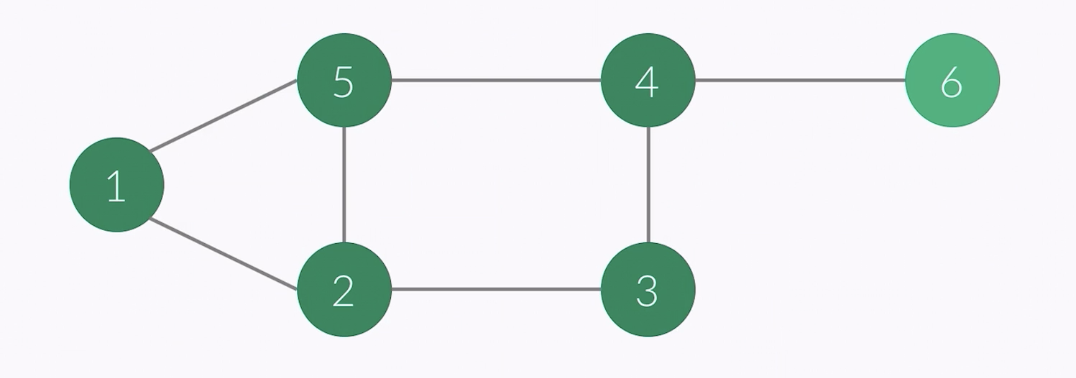
              - vertex of this point : 5
              - i ........... 1 2 3 4 5 6
              - check[i] 1 1 1 1 1 0
        • order : 1 2 3 4 5 6
        • stack : 1 2 3 4 6
          - it's all over now
          • once it over, people can know it's over but
            • stack goes popping one by one
            • after stack : 1 2 3 4
              - it can know that there is no vertex to go.
              - it is judged by checking if array 'check[i]'s value is 1 or 0
              - only if the value is 0, we can go to that number of vertex
              • it should pop the stack out
            • after stack : 1 2 3
            • after stack : 1 2
            • after stack : 1
            • after stack : empty
              - implement of DFS with Adjecency Matrix
  • time complexity = V * O(V) -> O(V^2)

        void dfs(int x) { // implemented recursively
            check[x] = true;
            printf("%d ", x);
            for (int i=1; i<=n; i++) {
                if (a[x][i] == 1 && check[i] == false) {
                    dfs(i);
                }
            }
        }

  • implement of DFS with Adjacency List
  • time complexity = O(V + E)

        void dfs(int x) {
        	check[x] = true;
            printf("%d ", x);
        	for (int i=0; i<a[x].size(); i++) {
            	int y = a[x][i];
            	if (check[y] == false) {
                	dfs(y); 
                }
            }
        }
    			```

• Algorithm of BFS
  - by using queue, it puts all the vertices which it can go to into queue
  • when it puts vertices into queue, it should check that number of vertex is in queue
    
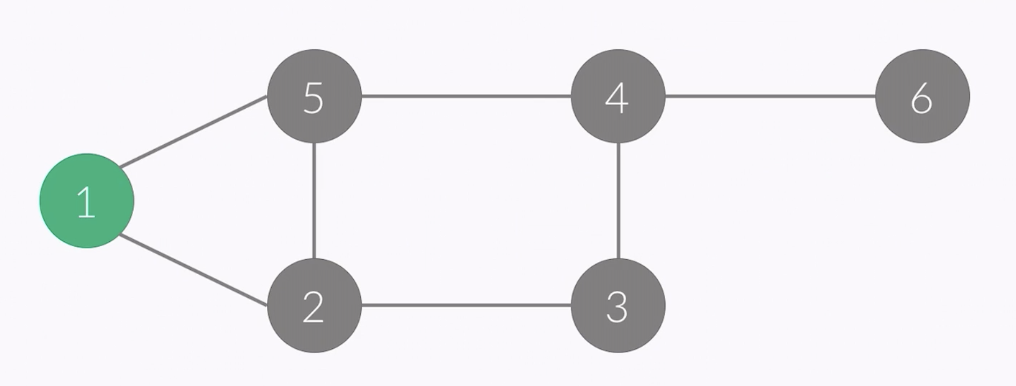
    - vertex of this point : 1
    - i ........... 1 2 3 4 5 6
    - check[i] 1 0 0 0 0 0
    - order : 1
    - queue : 1
    
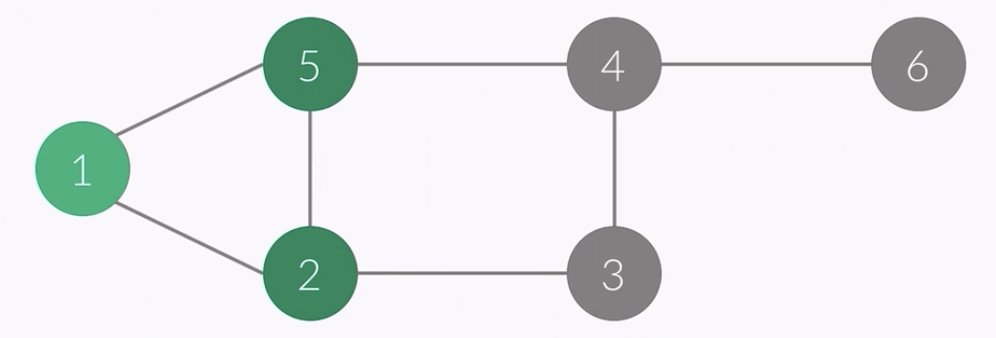
    - vertex of this point : 1
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 0 0 1 0
    - order : 1 2 5
    - queue : 1 2 5
    
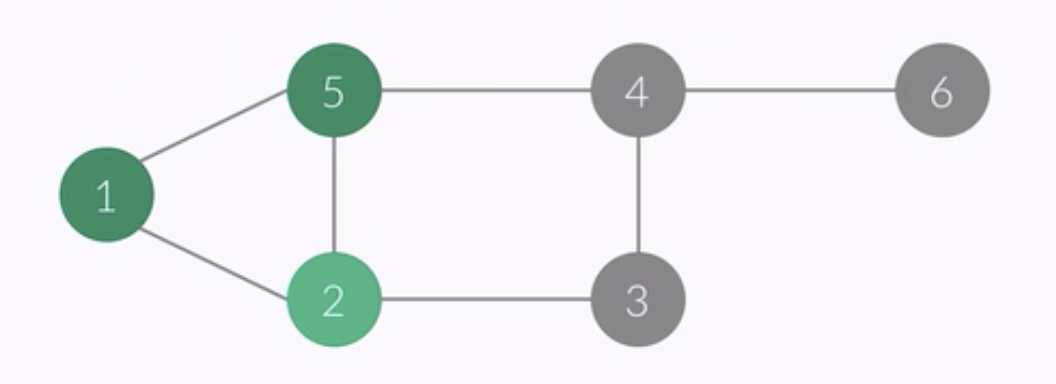
    - vertex of this point : 2
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 0 0 1 0
    - order : 1 2 5
    - queue : 2 5
    - in this case, it can't go to 5 because 5 has been already checked at this point.
    - so it saves only vertex number 3
    
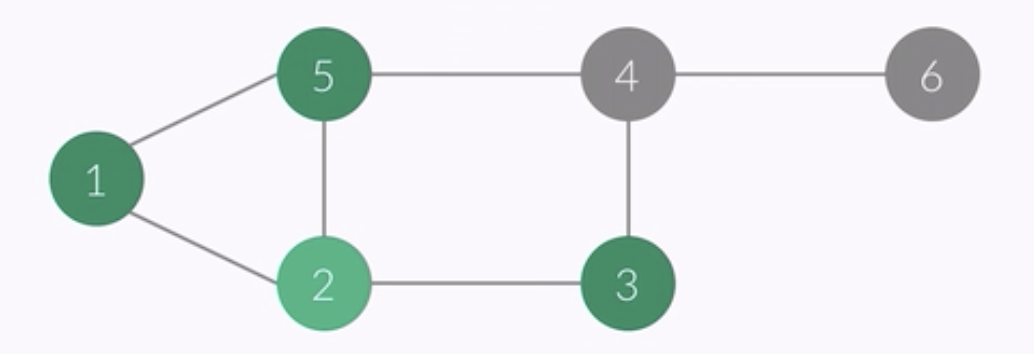
    - vertex of this point : 2
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 1 0 1 0
    - order : 1 2 5 3
    - queue : 2 5 3
    
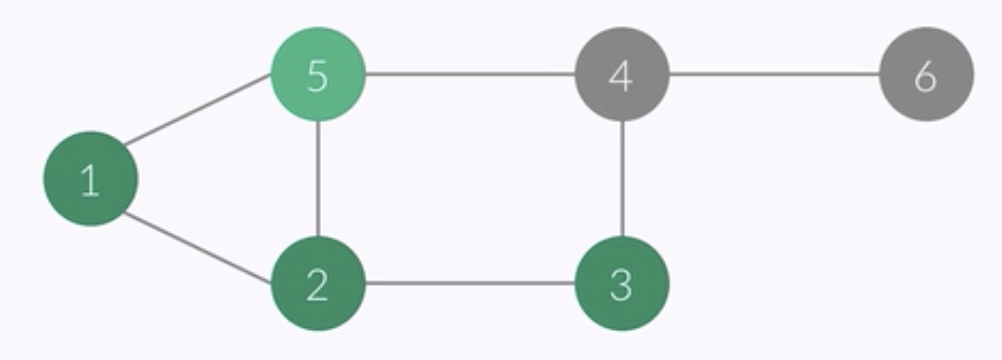
    - vertex of this point : 5
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 1 0 1 0
    - order : 1 2 5 3
    - queue : 5 3
    
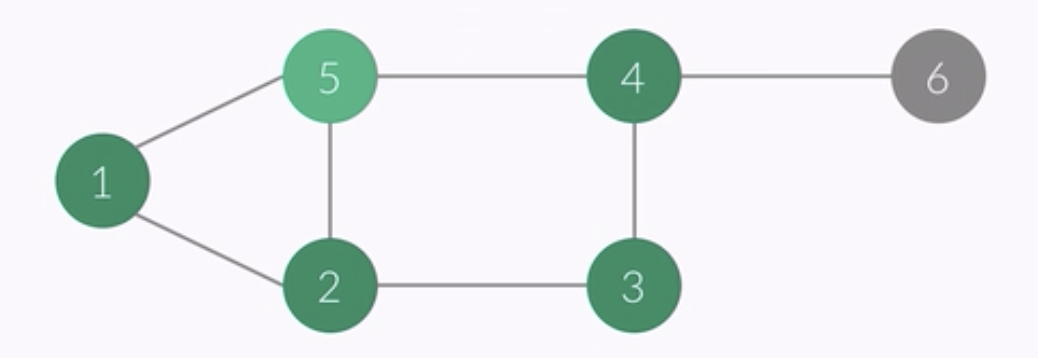
    - vertex of this point : 5
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 1 1 1 0
    - order : 1 2 5 3 4
    - queue : 5 3 4
    
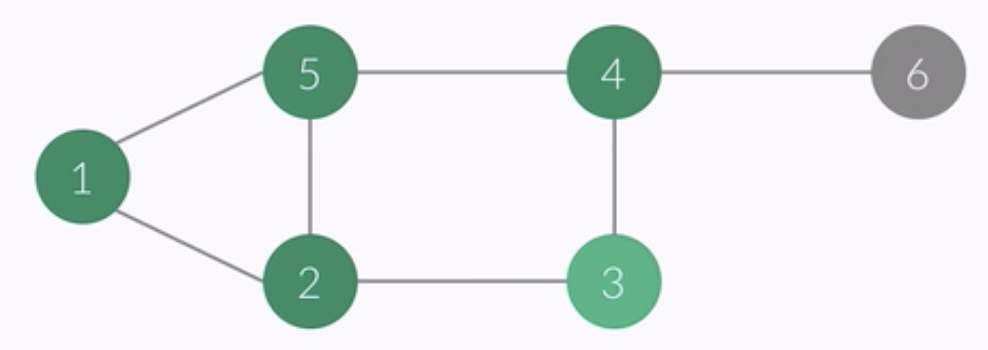
    - vertex of this point : 3
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 1 1 1 0
    - order : 1 2 5 3 4
    - queue : 3 4
    
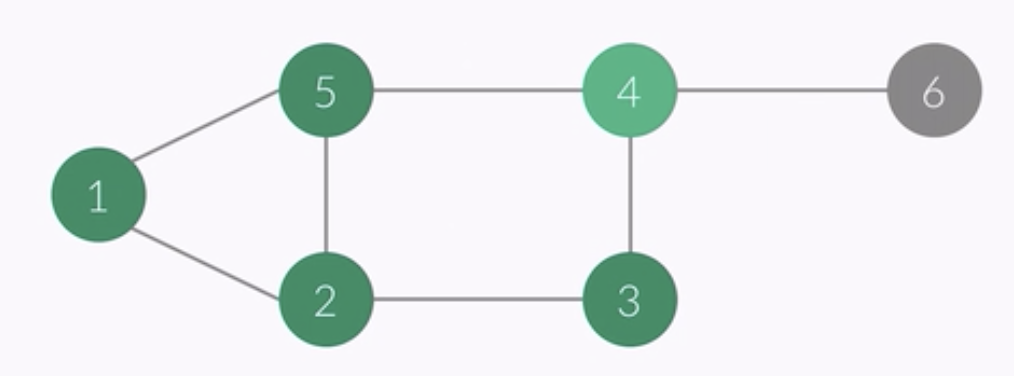
    - vertex of this point : 4
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 1 1 1 0
    - order : 1 2 5 3 4
    - queue : 4
    
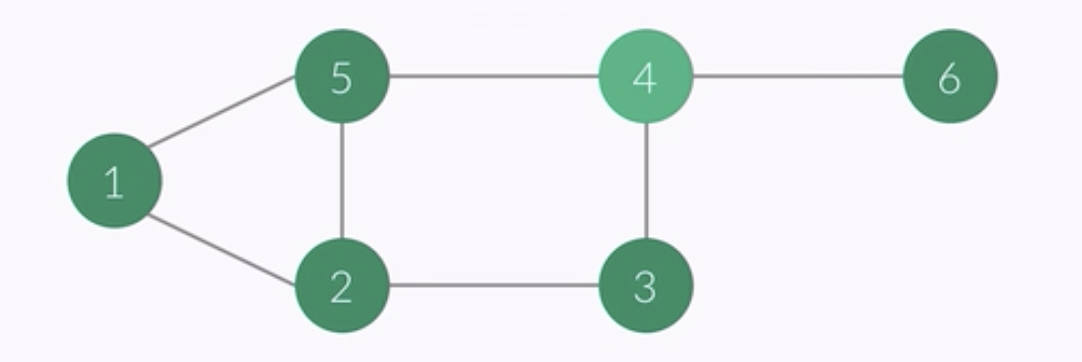
    - vertex of this point : 4
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 1 1 1 1
    - order : 1 2 5 3 4 6
    - queue : 4 6
    
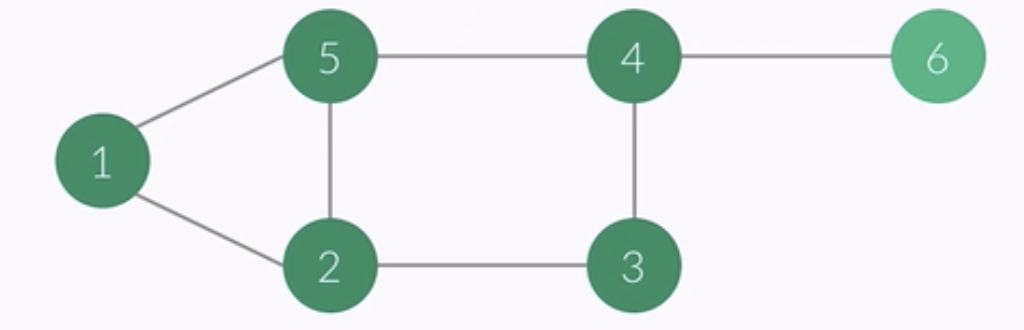
    - vertex of this point : 6
    - i ........... 1 2 3 4 5 6
    - check[i] 1 1 1 1 1 1
    - order : 1 2 5 3 4 6
    - queue : 6
    - implement of BFS with Adjacency Matrix

    			queue<int> q;
    			check[1] = true; q.push(1);
    			while(!q.empty()) {
    	int x = q.front(); q.pop();
    	printf("%d ", x);
    	for (int i=1; i<=n; i++) { // it's really similar to DFS, but DFS is implemented by recursive function
        	if (a[x][i] == 1 && check[i] == false) {
            	check[i] = true;
            	q.push(i);
            }
        }
      
    }

    		- implemented of BFS with Adjacency List

    			queue<int> q;
    			check[1] = true; q.push(1);
    			while (!q.empty()) {
    	int x = q.front(); q.pop();
    	printf("%d ", x);
    	for (int i=0; i<a[x].size(); i++) {
        	int y = a[x][i];
        	if (check[y] == false) {
            	check[y] = true; q.push(y);
            }
        }
    }
    			```

Problem implementing DFS and BFS

• boj.kr/1260

    import java.io.BufferedReader;
    import java.io.IOException;
    import java.io.InputStreamReader;
    import java.util.ArrayList;
    import java.util.Collections;
    import java.util.LinkedList;
    import java.util.StringTokenizer;

    public class Main {

        static boolean[] checkList;
        static int numOfVisitedVertices;
        static StringBuffer sb = new StringBuffer();

        public static void dfs(ArrayList<Integer>[] adjacentList, int startVertexNum, int numOfVertices){
            int currentVertexNum;
            for(int i=0; i<adjacentList[startVertexNum].size(); i++) {
                if(!checkList[adjacentList[startVertexNum].get(i)]) {
                    currentVertexNum = adjacentList[startVertexNum].get(i);
                    sb.append(currentVertexNum + " ");
                    checkList[currentVertexNum] = true;
                    numOfVisitedVertices++;
                    dfs(adjacentList, currentVertexNum, numOfVertices);
                }
            }
        }

        public static void bfs(ArrayList<Integer>[] adjacentList, int startVertexNum, int numOfVertices){

            LinkedList<Integer> queue = new LinkedList();
            queue.push(startVertexNum);

            while(!queue.isEmpty()){
                int currentVertexNum = queue.peekFirst();
                for(int i=0; i<adjacentList[currentVertexNum].size(); i++) {
                    int currentEdgeNum = adjacentList[currentVertexNum].get(i);
                    if(!checkList[currentEdgeNum]) {
                        queue.add(currentEdgeNum);
                        checkList[currentEdgeNum] = true;
                    }
                }

                sb.append(queue.poll() + " ");
            }
        }

        public static void main(String args[]) throws IOException {
            BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
            StringTokenizer st = new StringTokenizer(br.readLine());

            int numOfVertices = Integer.parseInt(st.nextToken());
            int numOfEdges = Integer.parseInt(st.nextToken());
            int startVertex = Integer.parseInt(st.nextToken());

            ArrayList<Integer>[] adjacentList = new ArrayList[numOfVertices + 1];

            for(int i=0; i<numOfEdges; i++){
                st = new StringTokenizer(br.readLine());

                int vNum = Integer.parseInt(st.nextToken());
                int eNum = Integer.parseInt(st.nextToken());

                if(adjacentList[vNum] == null) adjacentList[vNum] = new ArrayList();
                if(adjacentList[eNum] == null) adjacentList[eNum] = new ArrayList();

                adjacentList[vNum].add(eNum);
                adjacentList[eNum].add(vNum);
            }

            for(int i=1; i<=numOfVertices; i++)
                if(adjacentList[i] != null)
                    Collections.sort(adjacentList[i]);

            checkList = new boolean[numOfVertices + 1];
            checkList[startVertex] = true;
            numOfVisitedVertices = 1;
            sb.append(startVertex + " ");
            dfs(adjacentList, startVertex, numOfVertices);

            sb.append("\n");

            checkList = new boolean[numOfVertices + 1];
            checkList[startVertex] = true;
            bfs(adjacentList, startVertex, numOfVertices);

            System.out.print(sb);
        }
    }