밑바닥부터 시작하는 딥러닝 #2-1 신경망

Prologue

나는 여전히 웹개발자이지만, 회사에 부쩍 딥러닝 과제가 많아져서 딥러닝 공부가 많이 필요하게 됐다. 밑바닥부터 시작하는 딥러닝 책이 좋다고 해서 천천히 하나하나 공부해보려 한다.

신경망 개요

이전 시간에는 퍼셉트론을 알아봤습니다. 퍼셉트론의 귀찮은 특징 중 하나는 사람이 직접 가중치와 편향을 적절하게 조정해주어야 했던 점입니다. 신경망은 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습합니다.

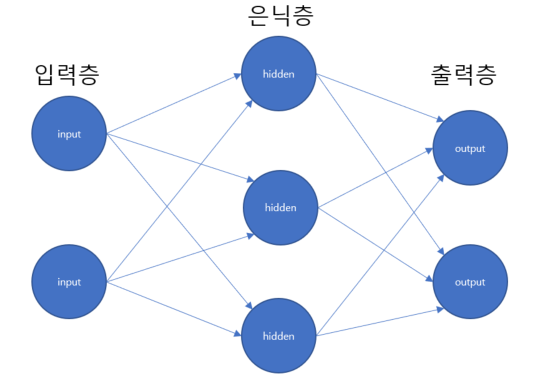
신경망은 위와 같은 형태로 구성됩니다. 총 3개의 층이 있는데, 0층에는 입력층, 1층에는 은닉층, 2층에는 출력층이 있습니다.

사실 우리는 퍼셉트론을 공부하며 위와 비슷한 그림을 본 적 있습니다. 그렇다면 퍼셉트론과 신경망의 차이는 무엇일까요? 그 차이를 공부하기 위해 잠시 퍼셉트론을 다시 떠올려봅시다.

퍼셉트론 복습

퍼셉트론은

1. 두 개의 입력을 받고
2. 가중치와 입력을 곱하고
3. 마지막으로 편향(bias)와 합해서
4. 세타(임계값)가 넘으면 1, 아니면 0

위와 같은 절차를 따랐습니다.

이를 수식으로 표현하면 다음과 같습니다.

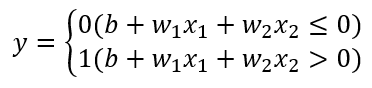
활성화 함수의 도입

이번에는 '활성화 함수'라는 새로운 함수를 도입해봅시다.

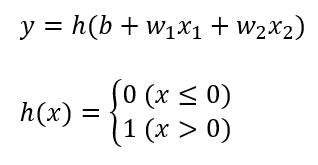
이전 퍼셉트론에서 y의 식을 활성화 함수 h(x)를 도입하여 쪼개봤습니다. y가 하는 일은 정확히 이전과 같습니다.

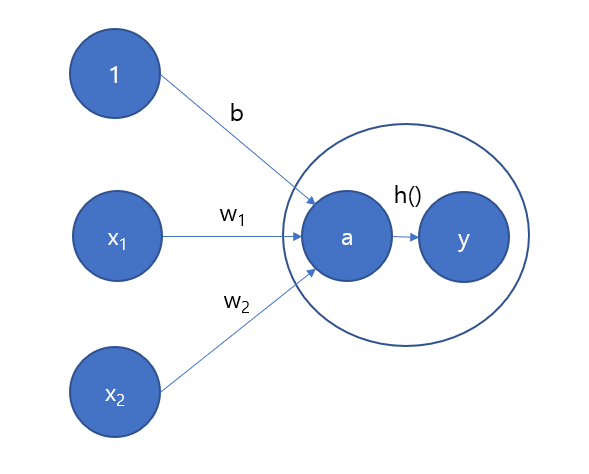
처리 과정을 시각화해보면 다음과 같습니다.

기존 가중치와 편향에 대한 신호를 합한 것이 a라는 뉴런(노드)가 되고, 활성화 함수 h()를 통과하여 y라는 출력 뉴런이 됩니다.

퍼셉트론에서 신경망으로

퍼셉트론과 신경망은 무슨 차이가 있는지 이제 정확히 정의해봅시다.

• 퍼셉트론
  1. 퍼셉트론은 일반적으로 '단층 퍼셉트론'을 가리킵니다.
  2. 퍼셉트론은 '계단 함수'라는 함수를 활성화 함수로 사용합니다.
• 신경망
  1. 신경망은 2개 이상의 퍼셉트론이 합쳐진 '다층 퍼셉트론'을 가리킵니다.
  2. 신경망은 '다양한 활성화 함수'를 골라쓸 수 있습니다.
  

다시 정리해보면, 퍼셉트론은 '단층'이며, '계단함수'를 활성화 함수로 사용하고, 신경망은 '다층'이며, '다양한 활성화 함수'를 골라씁니다.

'계단 함수'는 무엇이고 '다양한 활성화 함수'란 무엇일까요?

다양한 활성화 함수 소개

계단 함수

수식

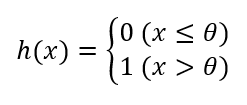
구현

def step(x):
	theta = 0
	return np.array(x > 0, dtype=np.int)

np.array의 마법이 있어서 가능한 코딩입니다. x>0은 bool타입 값인 TRUE를 반환하고, dtype에서 설정한 np.int가 TRUE를 1로 바꿔줍니다.

그래프

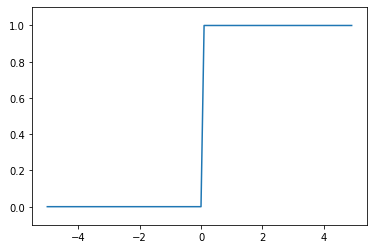
세타가 0인 케이스 입니다.

설명

퍼셉트론을 떠올려보면 쉽습니다. 세타를 넘기면 1 아니면 0입니다.

시그모이드 함수

수식

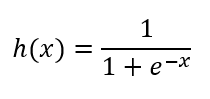
e는 자연상수 약 2.718xxx의 값입니다.

구현

def sigmoid(x):
	return 1 / (1 + np.exp(-x))

그래프

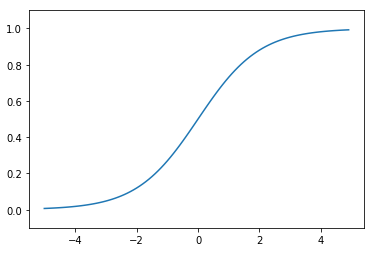
-5와 +5를 기점으로 0과 1이 됩니다.

설명

e의 -x제곱은 exp(-x) 로 표현되기도 합니다.

ReLU 함수

수식

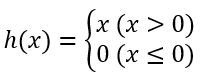
구현

def relu(x):
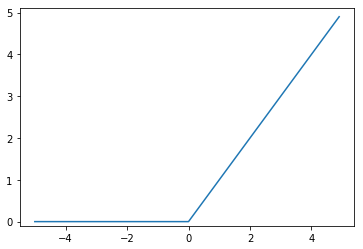
	return np.maximum(0, x)

그래프

시그모이드 함수와 계단 함수의 비교

• 차이점

  • 계단 함수는 입력 값이 세타를 넘기 전 0, 세타를 넘은 후 1이 되는 딱딱한 양상의 그래프를 보입니다. 반면 시그모이드는 -5보다 작지 않고, 5보다 크지 않은 값에 대해 부드럽게 0에서 1의 값을 반환합니다.

• 공통점

  • 둘 다 0에서 1 사이의 값을 반환합니다.
  • 둘 다 비선형 함수입니다.

비선형 함수

비선형 함수란 무엇일까요? 선형함수가 아닌 함수입니다.

선형함수란, 입력 값의 상수배를 출력 값으로 반환하는 함수를 말합니다. 수식으로는 일반적으로 아래와 같이 표현할 수 있습니다.

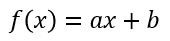
퍼셉트론에서 입력과 가중치 그리고 편향을 계산할 때의 식과 비슷합니다.

선형함수는 1개의 곧은 직선으로 표기가 가능합니다. 반면, 비선형 함수는 문자 그대로 '선형이 아닌 함수'입니다. 즉, 직선 1개로 그릴 수 없는 함수를 말합니다.

신경망에서는 활성화 함수로 비선형 함수를 사용해야 합니다. 만일, 선형 함수를 사용하면 신경망의 층을 깊게하는 의미가 사라집니다.

일례로 h(x) = cx일 때, y(x) = h(h(h(x)))라면, y(x) = c^3x와 같습니다.
그러므로, 선형 함수의 중첩은 활성화 함수 하나로 표현될 수 있습니다.
층을 쌓을 때는, 반드시 비선형 함수를 사용해야 의미가 있습니다.

numpy로 다차원 배열 다루기

행렬과 다차원 배열

2차원 배열은 행렬이라고도 부릅니다. 읽는 방법은 위와 같습니다. numpy는 2차원 배열 뿐만 아니라, 더 높은 차원의 다차원 배열도 지원합니다.

ndim

numpy의 내장함수 ndim은 해당 배열의 차원(dimension)을 반환합니다. 차원이란 하나의 배열에 몇개의 원소가 들어있는지를 말합니다.

shape

shape는 numpy로 만든 배열의 형상을 알려줍니다. (3, 2)는 총 3개의 배열로 이루어져있고, 그 배열 안의 내부 원소는 2개씩 있다는 것을 의미합니다. 내부 원소가 또 배열일 경우에는 계속하여 차원이 증가할 수 있습니다.

만일, 위의 케이스와 같이 배열 내부의 원소 개수가 일치하지 않으면 공백으로 표기합니다.

행렬 곱(내적)

행렬 곱에는 몇가지 조건이 있습니다.

1. A, B 행렬을 곱한다고 했을 때 A의 행(가로), B의 열(세로)을 곱한다.

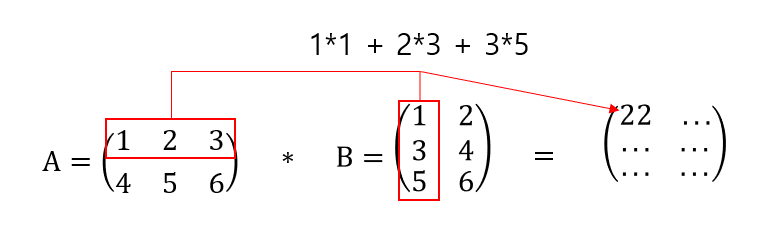
2. A, B 행렬을 곱한다고 했을 때 A의 행과 B의 열이 일치해야 한다.
   • shape의 결과로 나타내면 (5, 3) (3, 2)과 같이 일치해야 한다.

만일 A의 행(3)과 B의 열(3)이 일치하지 않는다면, 에러가 납니다.

다차원 배열의 경우에는 대응하는 차원의 원소 수를 일치시키면 됩니다.

넘파이를 이용한 신경망 구현

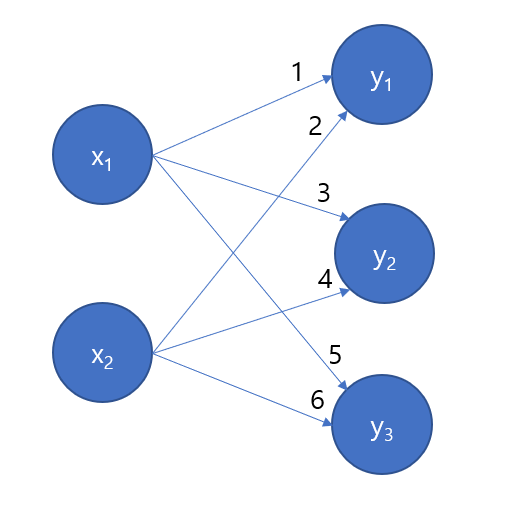
위의 1, 2, 3, 4, 5, 6은 가중치입니다. 위의 그림과 같은 신경망을 넘파이로 구현하면 아래와 같습니다.

위의 파이썬 코드는 X에 입력값으로 1, 2가 들어왔다고 가정하고 구현한 코드입니다. 그림과 같은 복잡해 보이는 신경망을 np.dot 함수를 이용하여 매우 쉽게 코드로 작성할 수 있습니다. 만일, np.dot이 없으면 for문으로 일일이 돌려야 하는 불상사가 생깁니다.

넘파이를 이용한 3층 신경망 구현

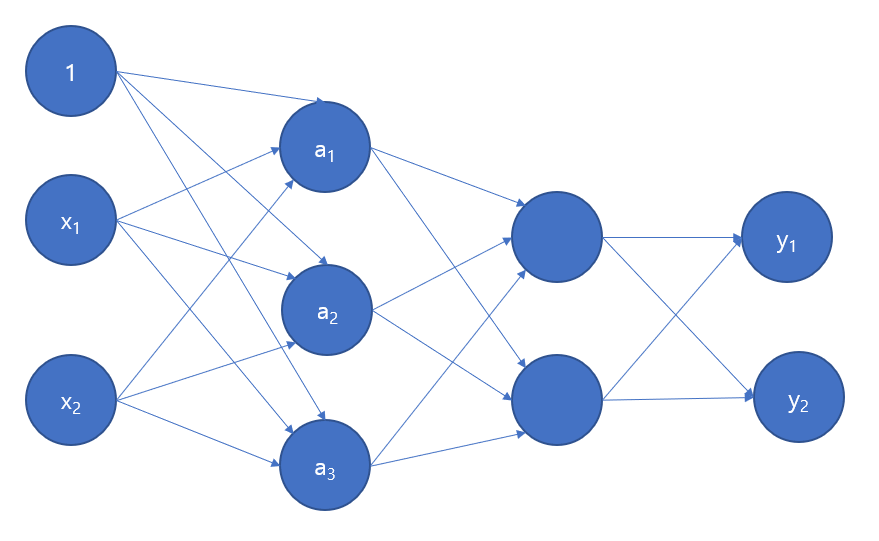
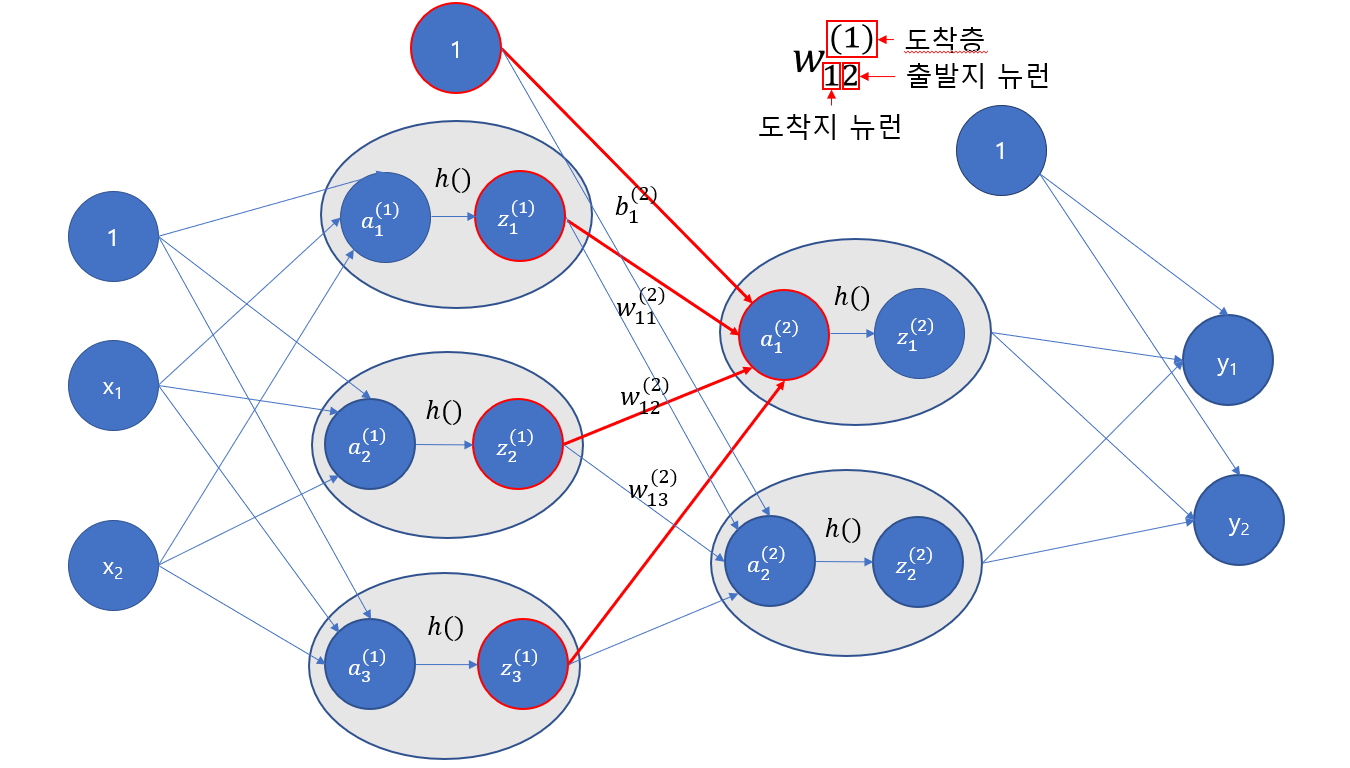
이렇게 생긴 신경망을 구현할 것입니다. 보기에는 매우 복잡해보이지만, 어떤 계산을 해야하는지 생각해보고 어떻게 행렬 혹은 다차원 배열로 표현할 것인지 떠올려본다면 대략적인 아이디어를 얻을 수 있습니다.

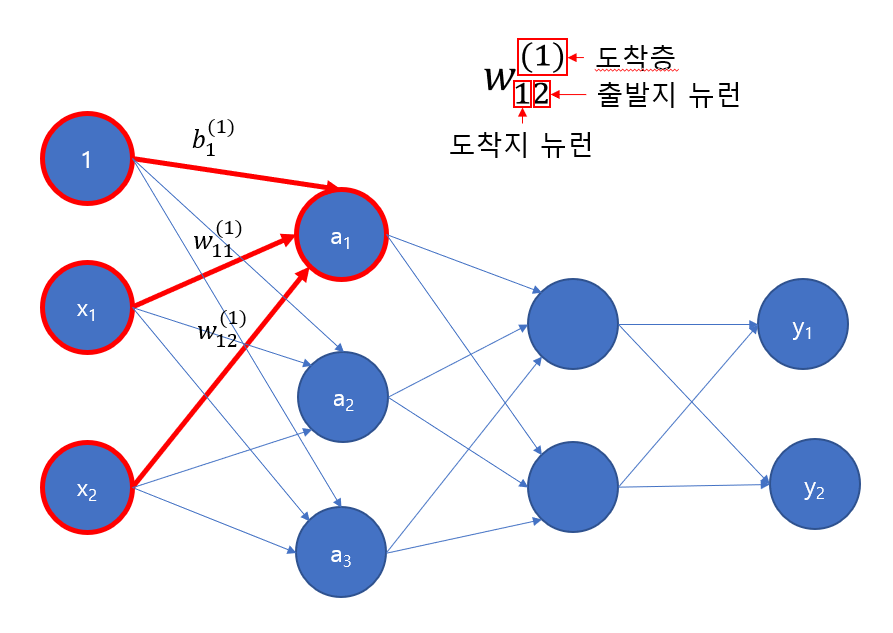
어떻게 계산할지를 생각해보면, a1, a2, a3 모두 3가지 값에 의해 연산이 되고 그 값은 각각의 입력값, 가중치, 편향에 의해 계산됩니다.

이전 퍼셉트론의 식을 이용하여 우리가 계산할 값들을 조금 일반화하면 공식이 나옵니다.

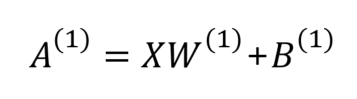
위와 같은 공식이 나오고 여기서 층 수가 더해지면 X를 이전 층의 A로 바꾸고 W와 B위의 (1)만 (2)로 바꿔주면 될 것입니다. 여기서 공식에 나온 변수를 일일이 행렬로 변경하면 다음과 같습니다.

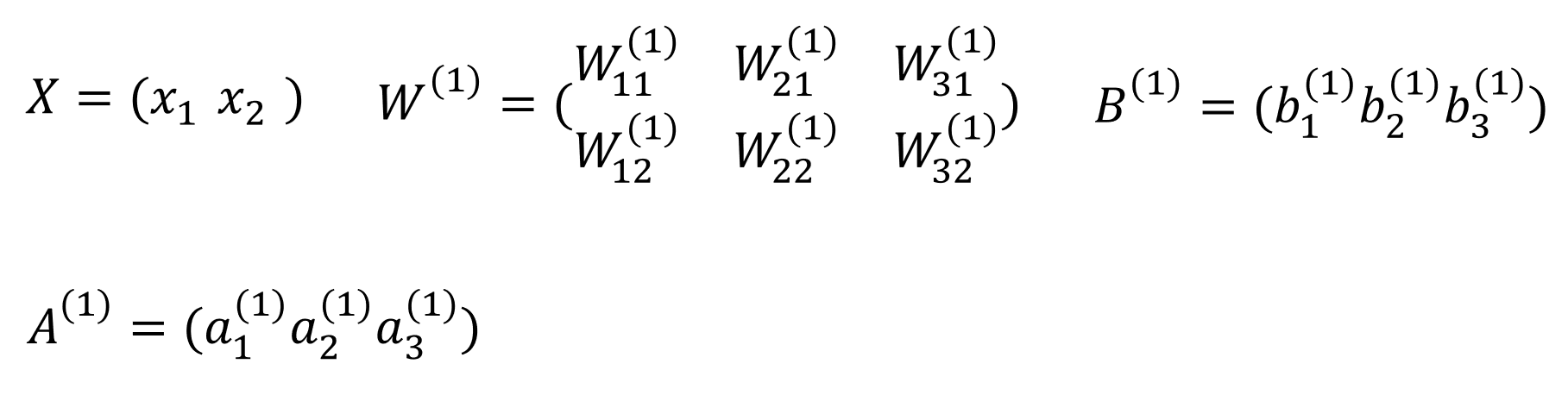
XWB를 곱하면 A가 나옵니다. 이걸 numpy로 구현하면 다음과 같은 코드가 나올 것입니다.

이제 가중치와 편향이 계산된 신호가 1층까지 도달했습니다. 다음으로 1층에 적용된 '활성화 함수'의 처리가 있습니다.

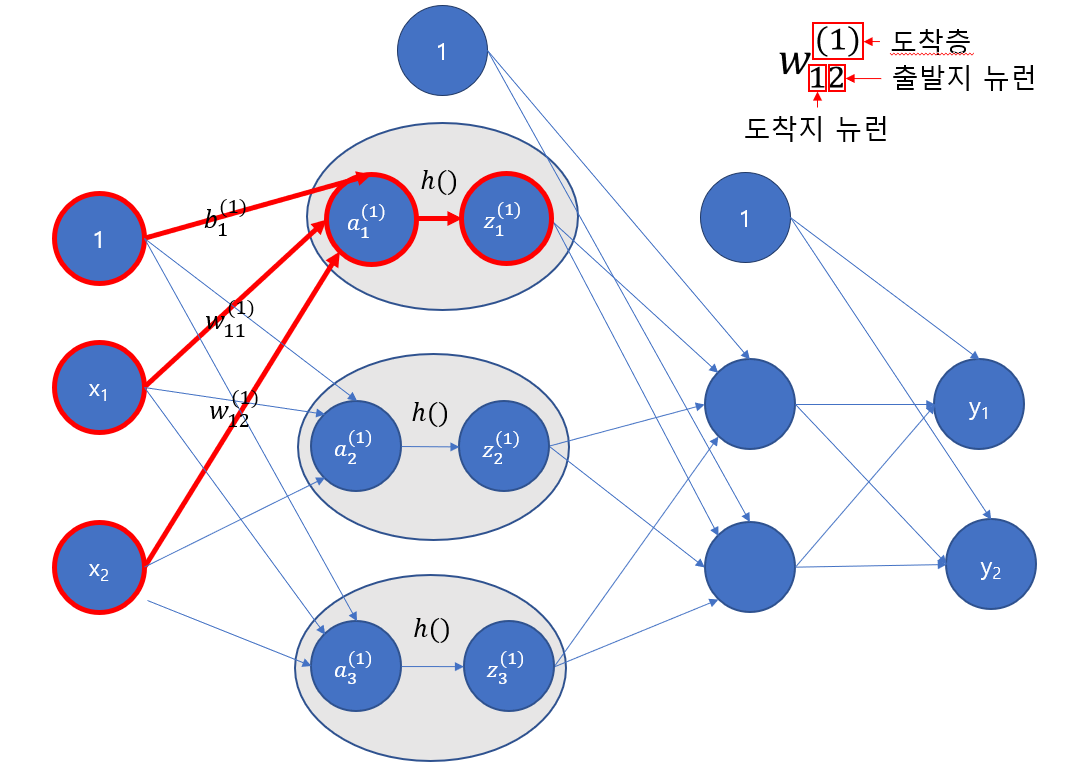
그림으로 표현하면 위와 같습니다. a는 가중치와 편향이 계산된 값이며, h()는 활성화 함수, z는 활성화 함수가 적용된 값입니다. 우리는 여기서 활성화 함수로 시그모이드 함수를 사용해보겠습니다.

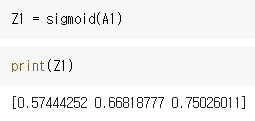
위와 같은 코드가 만들어지고, 결과는 Z1의 프린트 내역과 같습니다. 이후에 모든 시그모이드 처리를 한 결과 값 Z1에 가중치를 곱하고 편향을 더하여 다음 층으로 보냅니다.

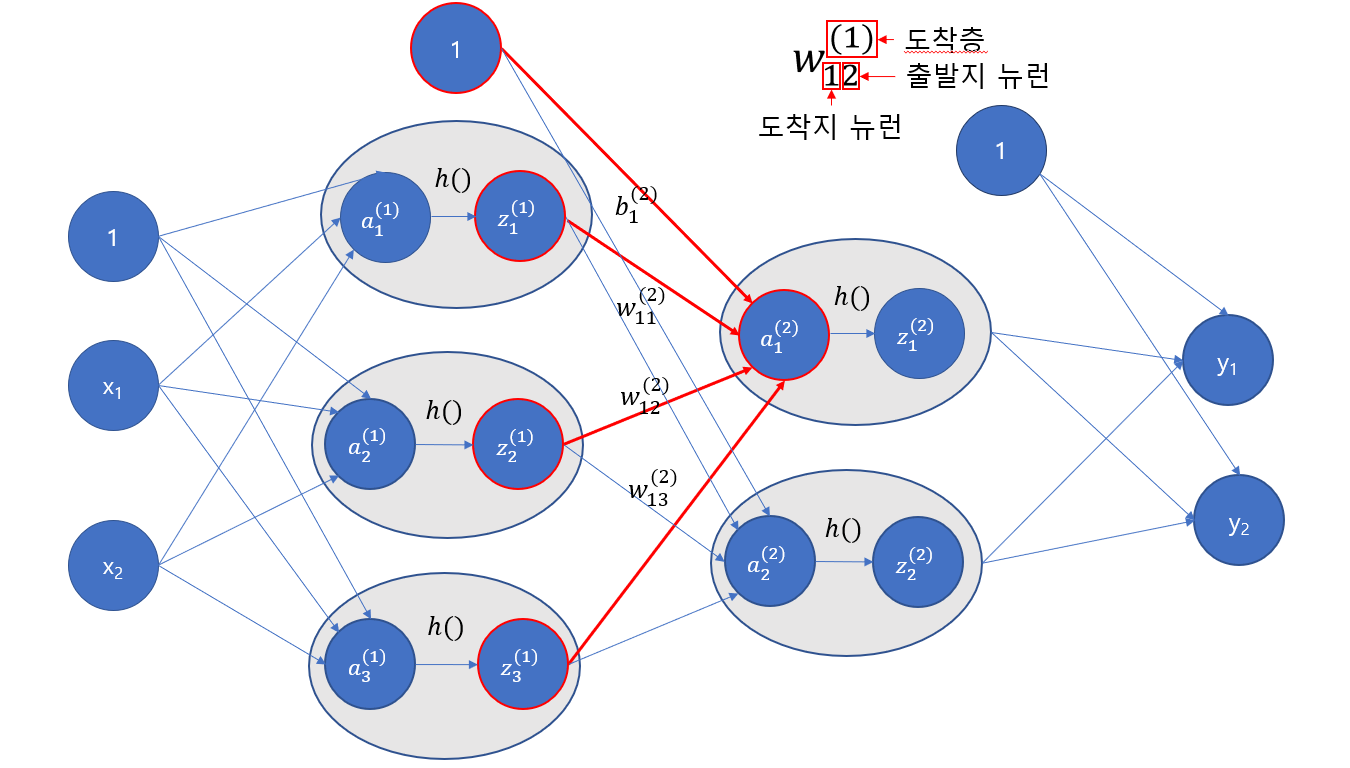
코드로 표현하면 다음과 같습니다.

다음으로 또 연산 값에 활성화 함수를 적용시켜줍니다.

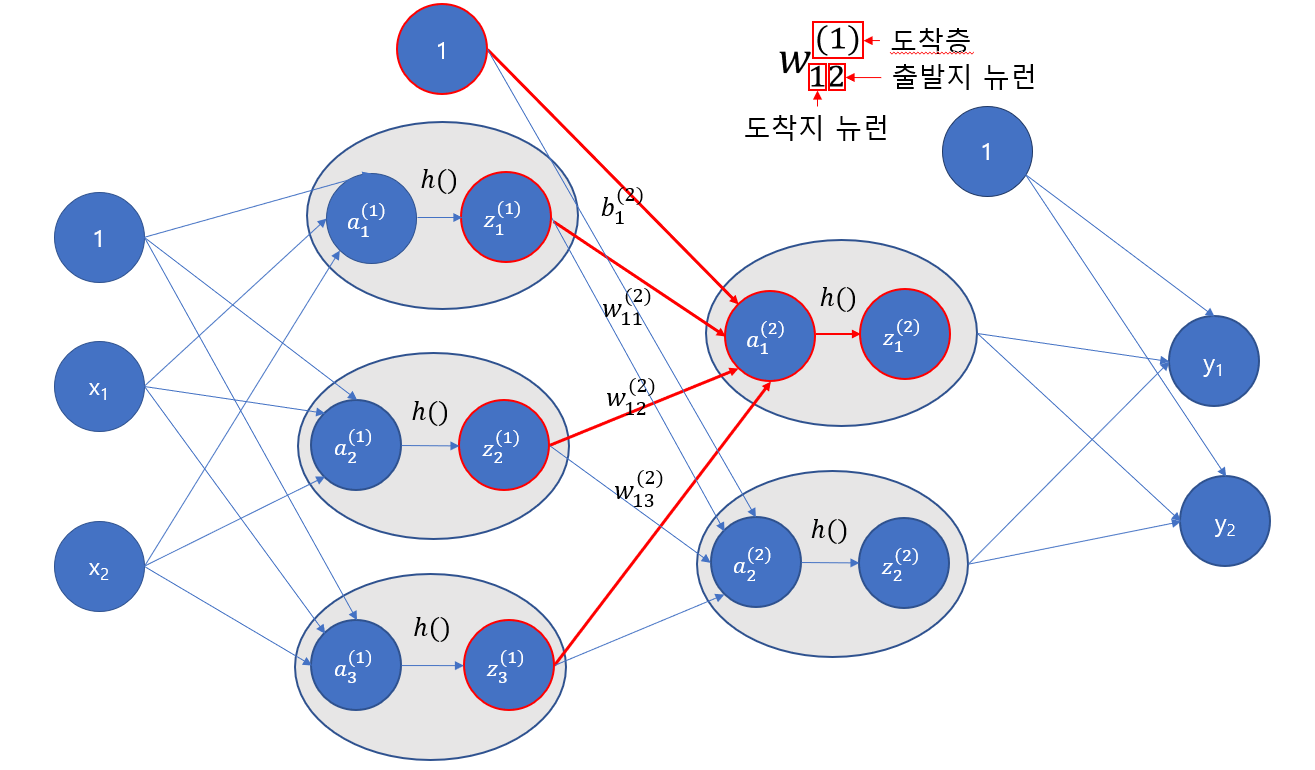
코드로 구현하면 다음과 같습니다.

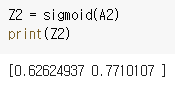
이제 마지막으로 2층에서 출력층으로 가는 일만 남았는데요. 출력층에서는 조금 특별한 활성화 함수를 사용합니다. 여기서 우리는 항등함수라는 것을 사용할 것입니다. 항등함수는 그냥 들어온 그대로 값을 반환해주는 함수입니다.

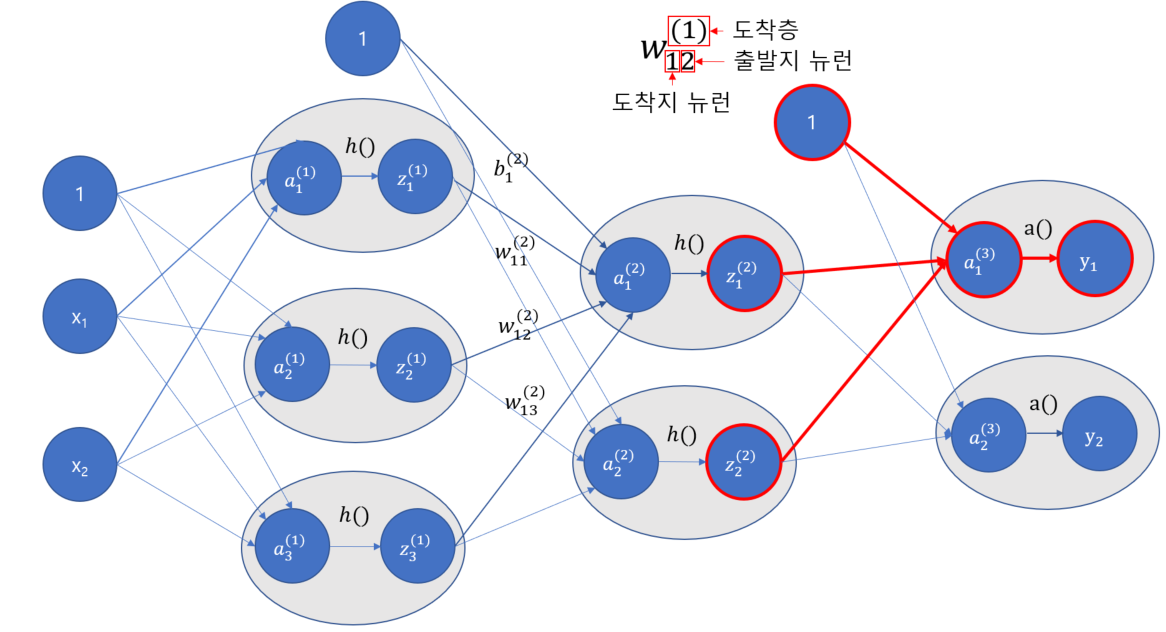
그림으로 표현하면 위와 같고, a() 라는 항등함수를 적용하기 때문에 z의 마지막 계산 값이 결국 y로 출력됩니다.

코드로 표현하면 위와 같습니다.

출력층의 활성화 함수는 풀고자하는 문제에 따라 달라집니다. 이진 분류에는 시그모이드 함수, 다중 분류에는 소프트맥스 함수를 사용하는 것이 일반적입니다.

위의 코드는 여태까지의 내용을 전부 코드로 묶은 겁니다.

'init_network'는 신경망에서 가중치와 편향을 초기화하는 것을 말하며, 'forward'는 순전파임을 의미합니다.

출력 활성화 함수인 소프트맥스 함수 구현하기

수식

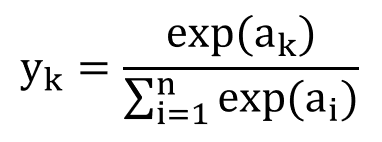
그림

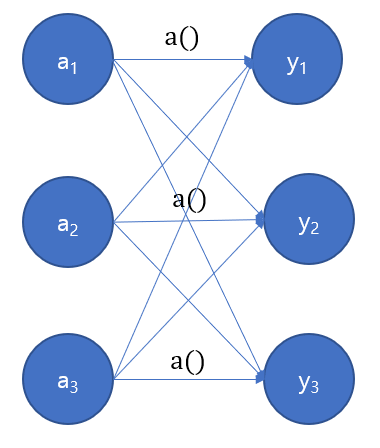
항등함수와는 다르게, softmax는 모든 출력에 영향을 미칩니다.

항등함수는?

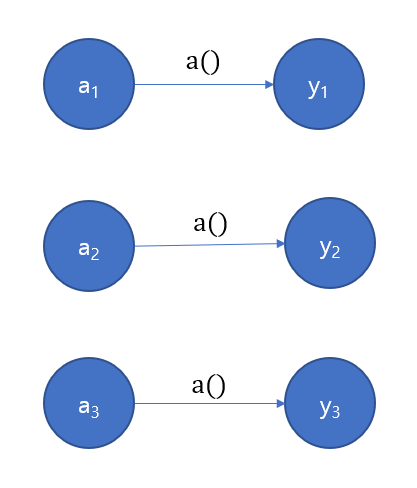
코드

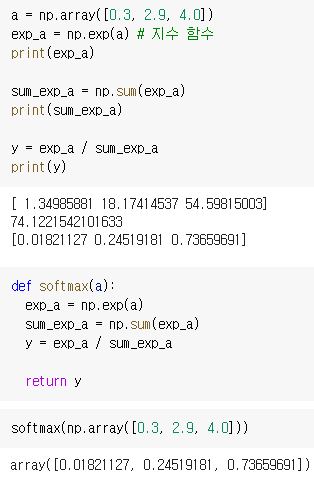
코드는 위와 같습니다. 전체를 더하고 그 전체로 각각을 나누면 됩니다.

개선된 소프트맥스 함수

기존 소프트맥스 함수의 문제점

• e의 범위로 인한 에러 발생

softmax 함수를 구현하는데에 들어가는 함수 중 하나인 np.exp()는 아주 쉽게 큰 값을 내뱉습니다. argument로 10만 들어가도 20,000이 넘는 값이 나오고 1000은 무한대를 뜻하는 inf가 됩니다.

개선된 수식

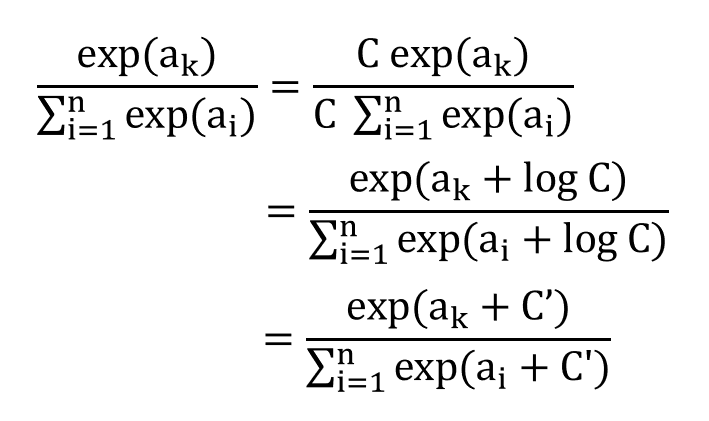
이 수식이 의미하는 것은, 분자 분모에 C라는 새로운 변수를 곱했을 때의 식의 진행을 말합니다. 여기서 +되는 C'는 보통 많은 a[i] 원소값중 가장 큰 값을 넣습니다.

개선된 코드

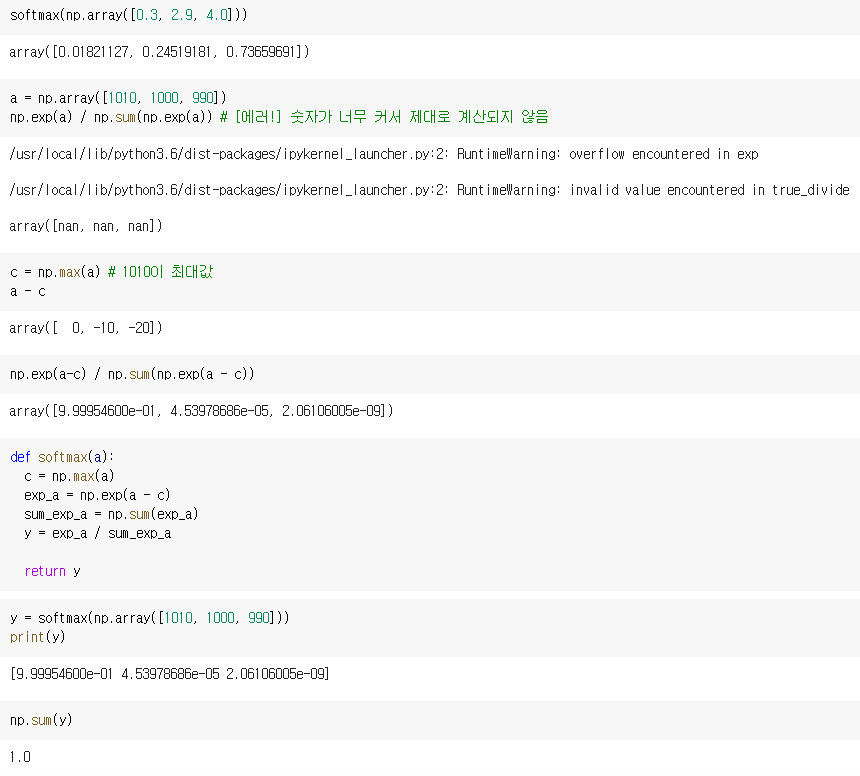
주의해서 볼 부분은 c = np.max(a) 로 최대 값을 가져오고, exp_a = np.exp(a - c)로 최대 값을 빼주는 부분입니다.

정리

1. '활성화 함수의 도입' 과 '다중 퍼셉트론의 사용' 은 신경망을 만듭니다.
2. 활성화 함수는 비선형적이어야 중첩의 의미 가 있습니다.
3. 비선형 활성화 함수는 ReLU, 시그모이드, 계단함수 등이 있습니다.
4. 출력 활성화 함수는 소프트맥스, 항등 함수 가 있습니다.
5. 분류 문제 에는 소프트맥스 함수가 적당하며, 회귀 문제 에는 항등함수가 적당합니다.