밑바닥부터 시작하는 딥러닝 정리 #1 퍼셉트론

Prologue

나는 여전히 웹개발자이지만, 회사에 부쩍 딥러닝 과제가 많아져서 딥러닝 공부가 많이 필요하게 됐다. 밑바닥부터 시작하는 딥러닝 책이 좋다고 해서 천천히 하나하나 공부해보려 한다.

퍼셉트론 개요

퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 것입니다. 여기서 퍼셉트론의 '신호'란 1(흐른다)과 0(안 흐른다) 두가지가 들어올 수 있습니다.

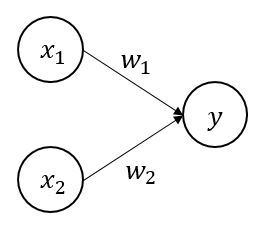
위 그림에서 x는 입력, y는 출력으로 볼 수 있습니다. x값이 입력되어 w라는 가중치와 곱해지고, 그 가중치가 일정 이상의 값(보통 Θ-세타라고 합니다.)을 초과하면 퍼셉트론의 신호는 '1(흐른다)'이 됩니다.

논리회로를 퍼셉트론으로 표현하기

위에서 퍼셉트론이 입력 x와 가중치 w 임계 기준 Θ(theta)를 갖는다는 것을 알았습니다. 우리는 들어오는 입력 값 x에 따라 가중치와 임계 값 Θ가 잘 작동하게 만들어서 논리회로인 AND, NAND, OR 등을 표현할 수 있습니다.

위는 AND회로를 구현한 것입니다. 입력값 2개(x1, x2)가 들어가서 출력 값을 만들어냅니다. 제가 모델을 만들기 위해 설정한 값은 가중치 w와 임계 값 Θ입니다.

가중치 w와 임계값 Θ만 잘 바꾸면 NAND도 OR도 전부 구현할 수 있습니다.

편향(bias) 도입하기

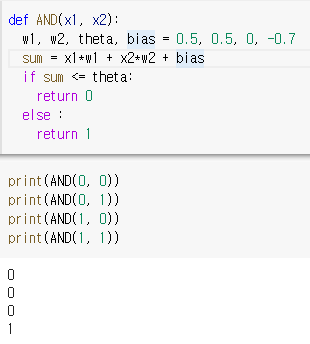
이전의 구현에서 bias라는게 추가되어서 결과 값에 마지막으로 더해지고 있습니다.
이 구현을 넘파이를 이용하여 구현하면 다음과 같습니다.

넘파이 배열의 곱셈에 대해 간단히 설명드리자면, 넘파이의 곱셈은 원소 수가 같을 경우에는 각각의 원소를 곱합니다.

위의 코드를 보시면 아시겠지만, 편향은 결국 얼마나 쉽게 활성화하느냐를 조정하는 매개변수가 됩니다.

일반적으로 w는 가중치 b는 편향이라고 하지만, 문맥에 따라 셋 모두를 '가중치'로 표현하는 경우도 있습니다.

위는 NAND와 OR를 구현한 것입니다.

(단일) 퍼셉트론의 한계

XOR게이트는 2개의 입력 값 중 1개만 TRUE일 때 활성화되는 게이트입니다. 이러한 XOR게이트를 만드려고 할 때, 퍼셉트론의 한계가 드러납니다.

먼저, OR게이트의 예를 보면서 생각해봅시다.

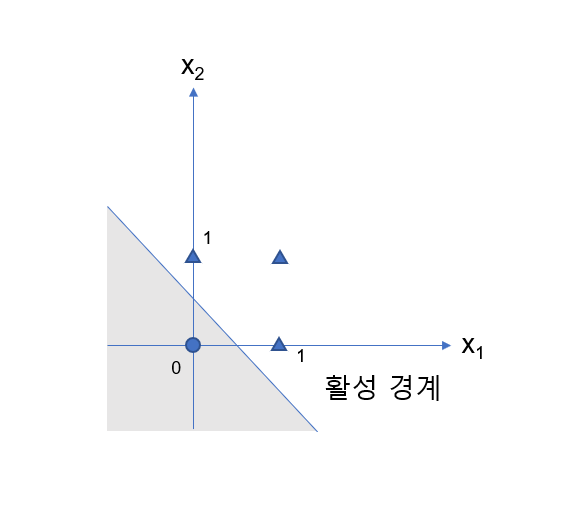
위 그림은 OR게이트 퍼셉트론을 시각화한 것입니다. x1, x2 두 개의 입력을 받고, 1개라도 1이면 1을 반환, 둘 다 1이면 1을 반환합니다.

회색 부분은 0을 반환하는 영역입니다.

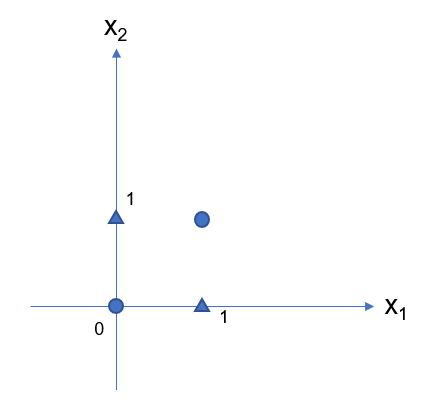
xor(입력값 1개가 1일 경우에만 출력값이 1인 게이트)의 경우, 경계선은 어디에 그리고, 회색 부분은 어디일까요? 직선으로 생각하면 답을 얻을 수 없습니다.

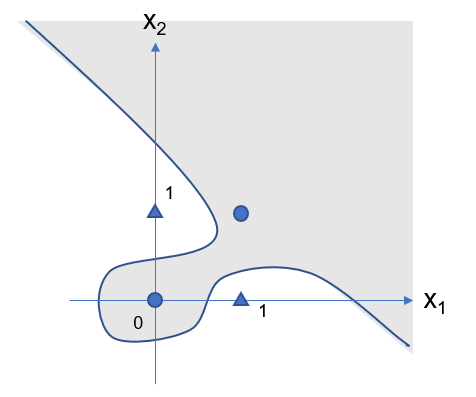
정답은 위와 같습니다.

이렇게 직선 말고 곡선으로 활성의 경계선을 긋고 싶다면, 퍼셉트론 하나로는 불가능하고 다층 퍼셉트론을 이용할 줄 알아야 합니다.

여태까지 만들어보았던, AND, NAND, OR를 합쳐서 다중 퍼셉트론을 만든다면, XOR 게이트를 구현할 수 있습니다.

위의 코드처럼 코딩하면 XOR 게이트를 얻을 수 있습니다.

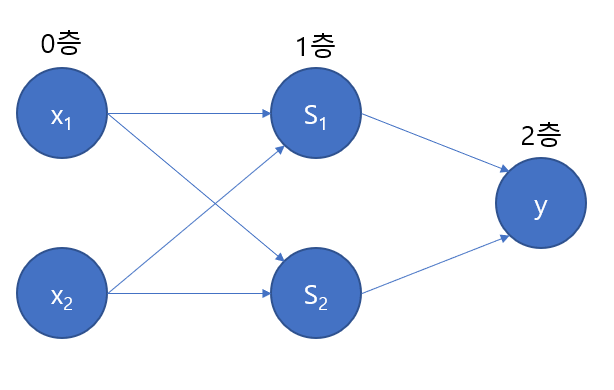
AND, OR가 단층 퍼셉트론인데 반해, XOR는 2층 퍼셉트론입니다. 이를 다중 퍼셉트론이라 합니다. 총 3층으로 볼 수도 있으나, 입력은 층으로 치지 말고 0층으로 봅시다.

퍼셉트론을 거듭 쌓으면, 비선형적인 표현도 가능하고, 이론상 컴퓨터가 수행하는 처리도 모두 표현 가능합니다.

요약

• 퍼셉트론은 입출력을 갖춘 알고리즘이다.
• 퍼셉트론에서는 '가중치'와 '편향'을 매개변수로 설정한다.
• 다양한 논리회로가 표현 가능하며, XOR는 다중 퍼셉트론으로 표현 가능하다.
• 단층 퍼셉트론은 직선형 영역, 다층 퍼셉트론은 비선형 영역도 표현할 수 있다.
• 퍼셉트론은 (이론상) 컴퓨터를 표현할 수 있다.