코딩테스트 #1 2019 카카오 개발자 겨울 인턴십 크레인 인형뽑기 게임

문제 설명

게임개발자인 죠르디는 크레인 인형뽑기 기계를 모바일 게임으로 만들려고 합니다.
죠르디는 게임의 재미를 높이기 위해 화면 구성과 규칙을 다음과 같이 게임 로직에 반영하려고 합니다.

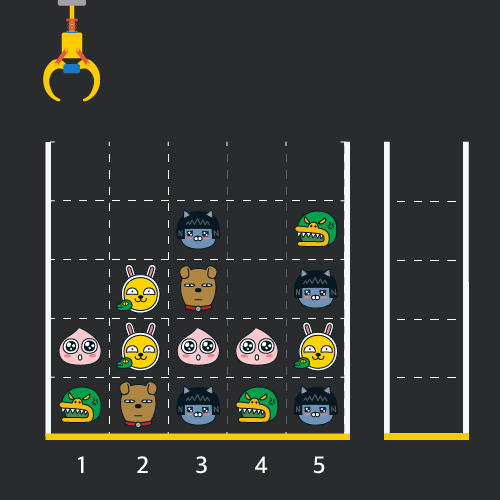
게임 화면은 1 x 1 크기의 칸들로 이루어진 N x N 크기의 정사각 격자이며 위쪽에는 크레인이 있고 오른쪽에는 바구니가 있습니다. (위 그림은 5 x 5 크기의 예시입니다). 각 격자 칸에는 다양한 인형이 들어 있으며 인형이 없는 칸은 빈칸입니다. 모든 인형은 1 x 1 크기의 격자 한 칸을 차지하며 격자의 가장 아래 칸부터 차곡차곡 쌓여 있습니다. 게임 사용자는 크레인을 좌우로 움직여서 멈춘 위치에서 가장 위에 있는 인형을 집어 올릴 수 있습니다. 집어 올린 인형은 바구니에 쌓이게 되는 데, 이때 바구니의 가장 아래 칸부터 인형이 순서대로 쌓이게 됩니다. 다음 그림은 [1번, 5번, 3번] 위치에서 순서대로 인형을 집어 올려 바구니에 담은 모습입니다.

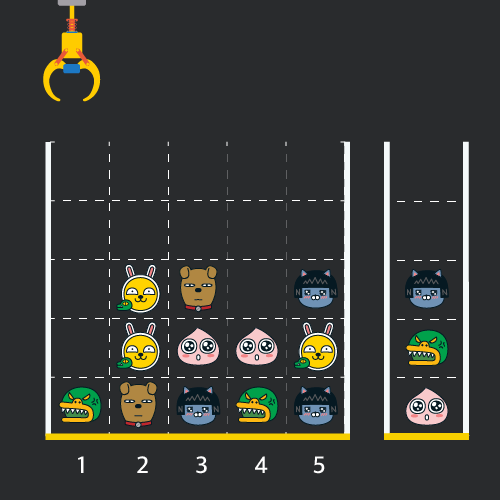
만약 같은 모양의 인형 두 개가 바구니에 연속해서 쌓이게 되면 두 인형은 터뜨려지면서 바구니에서 사라지게 됩니다. 위 상태에서 이어서 [5번] 위치에서 인형을 집어 바구니에 쌓으면 같은 모양 인형 두 개가 없어집니다.

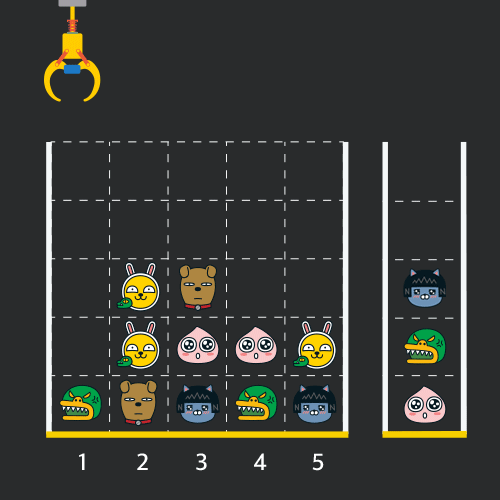
크레인 작동 시 인형이 집어지지 않는 경우는 없으나 만약 인형이 없는 곳에서 크레인을 작동시키는 경우에는 아무런 일도 일어나지 않습니다. 또한 바구니는 모든 인형이 들어갈 수 있을 만큼 충분히 크다고 가정합니다. (그림에서는 화면표시 제약으로 5칸만으로 표현하였음)

게임 화면의 격자의 상태가 담긴 2차원 배열 board와 인형을 집기 위해 크레인을 작동시킨 위치가 담긴 배열 moves가 매개변수로 주어질 때, 크레인을 모두 작동시킨 후 터트려져 사라진 인형의 개수를 return 하도록 solution 함수를 완성해주세요.

제한사항

• board 배열은 2차원 배열로 크기는 5 x 5 이상 30 x 30 이하입니다.
• board의 각 칸에는 0 이상 100 이하인 정수가 담겨있습니다.
• 0은 빈 칸을 나타냅니다.
• 1 ~ 100의 각 숫자는 각기 다른 인형의 모양을 의미하며 같은 숫자는 같은 모양의 인형을 나타냅니다.
• moves 배열의 크기는 1 이상 1,000 이하입니다.
• moves 배열 각 원소들의 값은 1 이상이며 board 배열의 가로 크기 이하인 자연수입니다.

입출력 예

board
[[0,0,0,0,0],[0,0,1,0,3],[0,2,5,0,1],[4,2,4,4,2],[3,5,1,3,1]]

moves
[1,5,3,5,1,2,1,4]

result
4

입출력 예에 대한 설명

입출력 예 #1

인형의 처음 상태는 문제에 주어진 예시와 같습니다. 크레인이 [1, 5, 3, 5, 1, 2, 1, 4] 번 위치에서 차례대로 인형을 집어서 바구니에 옮겨 담은 후, 상태는 아래 그림과 같으며 바구니에 담는 과정에서 터트려져 사라진 인형은 4개 입니다.

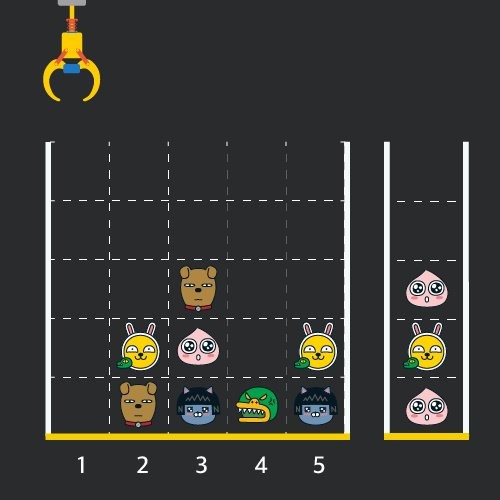
풀이

딱 봤을 때, 스택 이라는 자료구조가 바로 생각나는 문제입니다. 집게로 뽑을 인형이 들어갈 공간의 스택과, 뽑힌 인형이 들어있는 스택이 있습니다.

그런데 입출력 예에서 board의 값을 보면 [[0,0,0,0,0],[0,0,1,0,3],[0,2,5,0,1],[4,2,4,4,2],[3,5,1,3,1]]이런 식으로 구성이 되어 있습니다. 현재 board의 배열 값은 row(행)의 관점으로 표현되어 있습니다.

board의 가장 앞 배열 값이 [0, 0, 0, 0, 0]으로 되어 있다는 것은 맨 윗줄이 비어있다는 것이며 2번째 줄 부터는 차례로 인형이 들어가있습니다. board의 배열을 row라는 변수를 이용하여 표현하면, [row1, row2, row3, row4, row5]이런 식으로 볼 수 있습니다.

그런데, 인형뽑기의 집게는 row(행) 단위로 인형을 집어가지 않습니다. 집게는 옆에서 인형을 집어가는 것이 아니라 위에서 인형을 집어갑니다. 그래서 board의 값을 column(열) 의 관점으로 바꾸어주는 작업이 필요합니다.

그리고 board의 값을 column(열) 의 관점으로 바꿔주는 동시에 빈 공간은 제거해버릴 것입니다. 행과 열을 뒤바꾸는 이러한 일은 행렬에서 transpose 라는 행위로 할 수 있습니다.

이 문제를 풀기 위해서 사실 transpose 라는 것이 무엇인지 몰라도 됩니다.

그냥

[[0,0,0,0,0],[0,0,1,0,3],[0,2,5,0,1],[4,2,4,4,2],[3,5,1,3,1]]의 값 (위에서부터 행을 순차적으로 왼쪽에서 오른쪽으로 본 관점) 을

[[0,0,0,4,3],[0,0,2,2,5],[0,1,5,4,1],[0,0,0,4,3],[0,3,1,2,1]]의 값 (왼쪽에서부터 열을 위에서 아래로 본 관점)으로 바꿔야 한다는 것만 알면 됩니다.

제한사항에 이 인형이 들어가는 박스는 NxN의 정사각형 이라는 말이 있습니다. 정사각형의 값을 transpose 하기 위해서는 javascript의 맵 함수를 사용하여 매우 간단하게 구현할 수 있습니다. 물론 for문을 중첩으로 사용하는 것도 좋습니다.

function transposeSqaure(s) {
	return s.map((_, index) => s.map($ => $[index]));
}

정확히 한줄로 구현이 가능한데, [행x열]만큼 반복하며 [x, y]와 같이 구성되어있던 값을 [y, x]로 좌표를 반대로 바꾸어 재구성한다고 생각하면 쉽습니다.

[[1, 2], [3, 4]]와 같은 값이 있으면 2차원 배열의 관점에서 1은 0,0 2는 0,1 3은 1,0 4는 1,1과 같은 좌표를 갖고 있습니다. 여기서 transpose를 가하게 되면, x,y 를 그대로 바꾼 [[1, 3], [2, 4]]가 됩니다.

이렇게 transpose 를 완료하고 추가적으로 0이라는 빈 공간은 우리가 고려할 필요가 없으니 다 지워줍시다.

그러면 함수는 다음과 같습니다.

function transposeSqaureAndRemoveZero(s) {
	return s.map((_, index) => s.map($ => $[index]).filter((_) => _ !== 0));
}

다음으로는 move에 있는 숫자에 맞춰 인형을 뽑으면 됩니다. 입출력 예제에는 [1, 5, 3, 5, 1, 2, 1, 4]라는 값이 들어있습니다.

인형을 뽑을 때는 배열의 가장 앞 원소를 지우며 리턴하는 shift 메소드를 이용하면 됩니다.

이제 moves 변수에 맞추어 인형을 뽑는 함수를 작성해봅시다.

function grabDolls(transposedBoard, moves){
    let vanishedDolls = 0; // 사라진 총 인형의 수
    let stackedDolls = []; // 뽑혀서 쌓인 인형의 배열
    
    moves.map((move) => {
        // 쌓인 인형의 수
        let stackedDollsCount = stackedDolls.length;
      	// 만일 집게가 간 열에 인형이 존재한다면, (인형이 없을 수 있음)
        if(transposedBoard[move-1].length > 0){
            // 집게에 잡힌 인형은 첫번째 인형
            let grabbedDoll = transposedBoard[move-1].shift();
            // 쌓인 인형이 있고, 맨 위에 쌓인 인형이 집게에 잡힌 인형과 같은 인형이라면 쌓인 인형 없애기
            if(stackedDollsCount > 0 && 
                stackedDolls[stackedDollsCount-1] 
                === grabbedDoll){
                stackedDolls.pop();
                // 인형은 한번에 2개씩 사라지기 때문에 2개 더하기
                vanishedDolls += 2;
            }else {
                // 만일 쌓여있던 인형과 일치하지 않으면 인형을 그냥 쌓기
                stackedDolls.push(grabbedDoll);
            }
        }
    });

    // 총 사라진 인형이 정답
    return vanishedDolls;
}

설명을 위해 일부러 변수명을 길게 적어봤는데 다른분들이 보았을 때 이해가 쉬웠으면 좋겠습니다.