3. Digital Signatures

Digital Signatures

Digital signatures are cryptographic mechanisms used to verify the authenticity and integrity of digital messages or documents. One popular digital signature scheme is the Schnorr signature scheme. Below is an overview of how it works:

Schnorr Signature Scheme

Watch an explanation here.

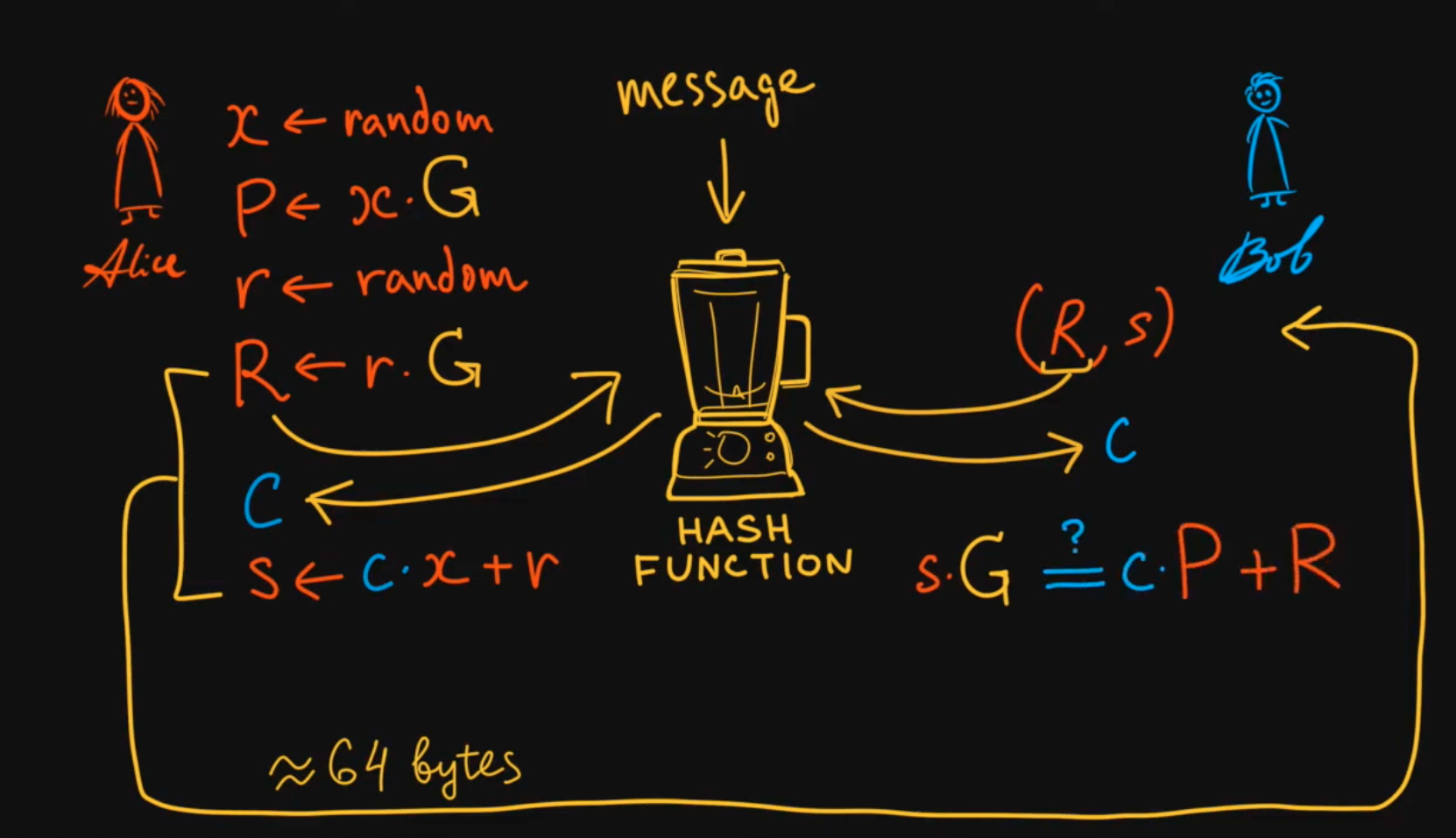
1. Key Generation:

• Generate Private Key $(sk)$: Select a random private key $x$ from the range $[1, n - 1]$, where $n$ is a large prime number.
• Compute Public Key $(pk)$: Calculate the public key $P = g^{x} \mod p$, where $g$ is a generator of a cyclic group of order $n$ in a finite field $F_p$.

2. Signing:

To sign a message $m$:

• Generate a Random Nonce $(k)$: Select a random integer $k$ from the range $[1, n - 1]$.

• Compute the Commitment: Calculate $R = g^{k} \mod p$.

• Compute the Hash: Calculate $e = H(R \parallel m)$, where $H$ is a cryptographic hash function and $\parallel$ denotes concatenation.

• Compute the Response: Calculate $s = k + e \cdot x \mod n$.

The signature on the message $m$ is the pair $(R, s)$.

3. Verification:

To verify a signature $(R, s)$ on a message $m$:

• Compute the Hash: Calculate $e = H(R \parallel m)$.

• Compute the Expected Commitment: Calculate $R' = g^{s} \cdot P^{-e} \mod p$.

• Verify the Commitment: Check if $R' = R$. If they are equal, the signature is valid.

Security Properties

• Unforgeability: The security of Schnorr signatures relies on the hardness of the discrete logarithm problem. Given $g$ and $P$, it is computationally infeasible to find $x$.

• Non-repudiation: Only the holder of the private key $x$ can generate a valid signature for a given message $m$.

• Integrity: If a signature $(R, s)$ on a message $m$ verifies correctly, it ensures that the message has not been altered.

Benefits

• Efficiency: Schnorr signatures are computationally efficient for both signature generation and verification.

• Compactness: Schnorr signatures are relatively short, making them suitable for systems with bandwidth or storage constraints.

Applications

• Cryptocurrencies: Schnorr signatures are used in some cryptocurrency protocols to improve efficiency and security.

• Authentication: They are employed in various authentication protocols, including secure communications and access control.

Conclusion

Schnorr signatures provide a robust and efficient method for ensuring the authenticity and integrity of digital data, making them a valuable tool in modern cryptography.