Hash Functions
A hash function is a cryptographic algorithm that takes an input (or "message") of any size and produces a fixed-size output, known as a message digest or digital fingerprint. This output is designed to be unique to the input data, and it’s nearly impossible to reverse-engineer the original input from the output.
Key properties of a good hash function:
- Deterministic: The same input will always produce the same output.
- Non-invertible: It is computationally infeasible to derive the original input from its output.
- Fixed Output Size: Regardless of the input size, the output is always of a fixed length.
- Collision-Resistant: It’s highly unlikely for two different inputs to produce the same output.
Common use cases for hash functions:
- Data Integrity Verification: Ensuring data has not been altered.
- Password Storage: Securely storing hashed passwords.
- Digital Signatures: Verifying the authenticity of digital documents.
- Cryptocurrencies: Used in systems like Bitcoin for transaction verification.
Popular hash functions include:
- SHA-1: Secure but now considered weak against modern attacks.
- SHA-2: Includes SHA-256 and SHA-512, widely used and secure.
- MD5: Considered broken and unsuitable for cryptographic purposes.
- bcrypt: Specifically designed for securely hashing passwords.

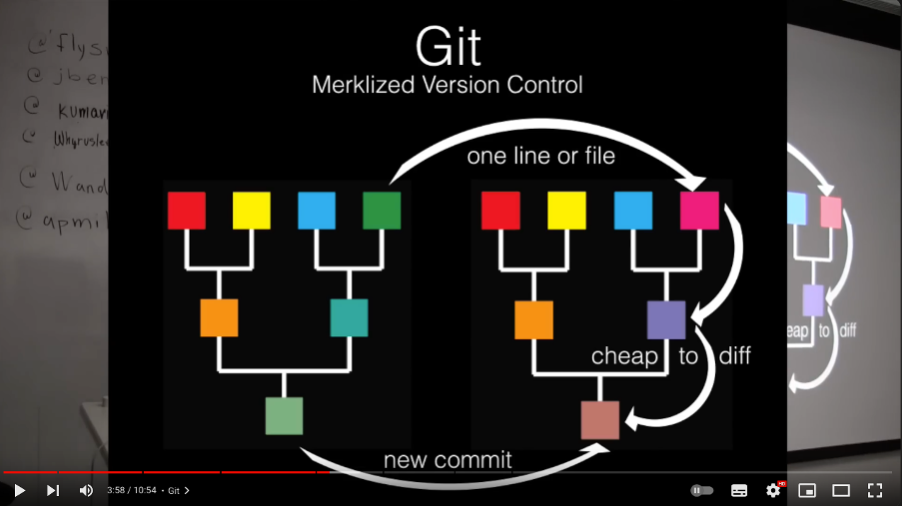
Merkle Trees
A Merkle tree, named after cryptographer Ralph Merkle, is a data structure that uses hash functions to verify the integrity and consistency of large datasets. It’s particularly useful for efficiently verifying large amounts of data without needing to check each individual piece.
How a Merkle Tree works:
- Data Chunking: Split the data into smaller chunks (e.g., files, blocks).
- Hashing: Compute a hash for each chunk using a cryptographic hash function.
- Pairing and Hashing: Combine the hashes of two adjacent chunks and hash the result to create a new node. Repeat this for all pairs to build a new level of the tree.
- Building the Tree: Continue combining and hashing nodes until you reach a single node at the top, known as the root hash or Merkle root.
Properties of Merkle Trees:
- Efficient Verification: To verify data integrity, only the hashes along the path from a leaf node to the root need to be checked.
- Scalability: Can handle large datasets with minimal computational overhead.
- Data Deduplication: Identical subtrees can be pruned, reducing storage requirements.
Applications of Merkle Trees:
- Blockchain: Used in blockchain technologies like Bitcoin and Ethereum to efficiently store and verify transactions while minimizing storage needs.
- Data Integrity: Ensures the integrity of large datasets by computing a root hash that acts as a compact representation of the data's authenticity.
- Digital Signatures: Enables efficient digital signatures, where signing the root hash validates the entire dataset.
In summary, hash functions provide a secure way to generate a unique identifier for data, while Merkle trees organize these identifiers into a structure that allows for efficient storage and verification of large data sets, ensuring their integrity.