7. BLS signature (BLS12-391)

BLS (Boneh-Lynn-Shacham) signatures are a type of digital signature scheme that utilizes pairings on elliptic curves to provide efficient and secure authentication. Developed by Dan Boneh, Ben Lynn, and Hovav Shacham in 2001, BLS signatures have gained popularity due to their efficient verification process, compactness, and support for signature aggregation.

Key Points:

• Multisig Challenges: Traditional multisignature schemes require several communication rounds, which can be cumbersome, especially with cold storage setups. BLS signatures simplify this by enabling a more straightforward aggregation process.

• Random Number Generation: In BLS signatures, the reliance on random number generators can be a concern since deterministic signing methods (like in ECDSA) are not applicable.

• Complexity in m-of-n Multisig: Implementing an m-of-n multisignature scheme with BLS requires creating a Merkle tree of public keys, which can become unwieldy as $m$ and $n$ increase.

• Signature Aggregation: While BLS allows for the aggregation of signatures, not all signatures within a block can be combined into a single signature, which can be a limitation in some contexts.

BLS Signature Scheme Overview:

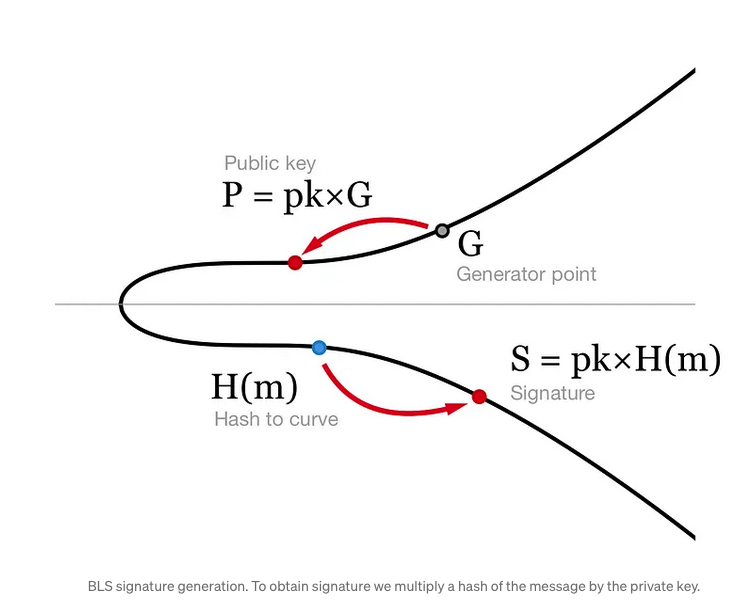
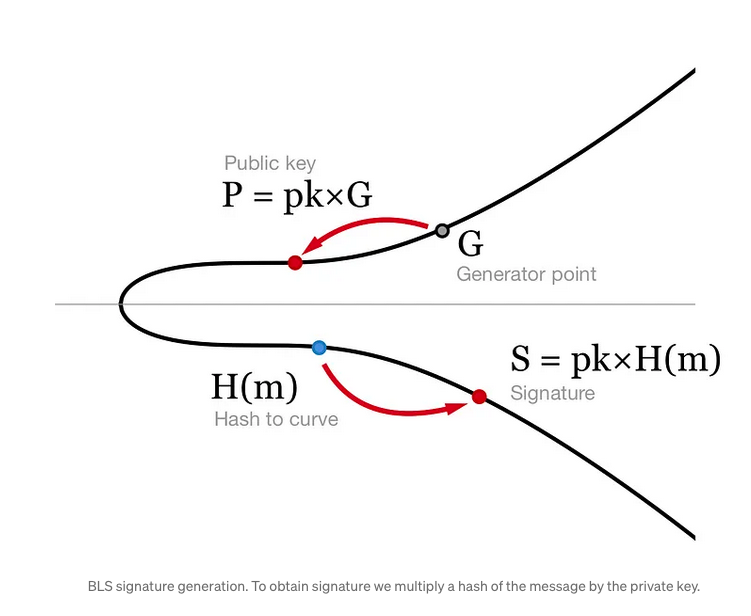
1. Key Generation:

   • A user generates a private key $sk$ and computes the corresponding public key $pk$ by multiplying $sk$ with a generator point $G$ on the elliptic curve.

2. Signing:

   • To sign a message $m$, the user hashes $m$ to a point on the elliptic curve using a cryptographic hash function $H(m)$.
   • The signature $\sigma$ is computed as $\sigma = sk \cdot H(m)$.

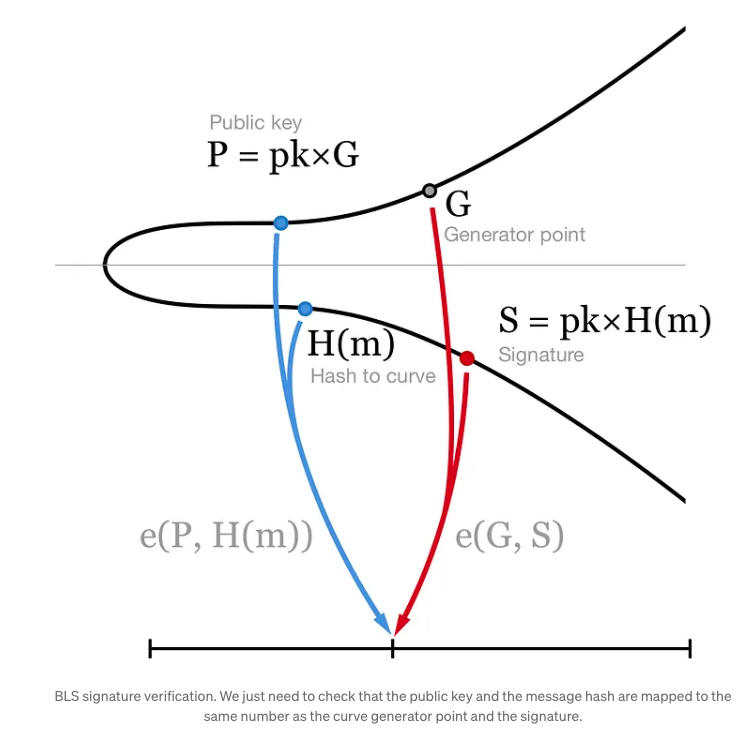
3. Verification:

   • The verifier checks the validity of the signature $\sigma$ by verifying the pairing equation:
     $e(\sigma, G) = e(H(m), pk)$
   • Here, $e$ is a bilinear pairing function, and $G$ is the generator point on the elliptic curve.

Advantages of BLS Signatures:

1. Fast Verification: The verification process in BLS is faster than in many other signature schemes, such as ECDSA, due to the efficient use of bilinear pairings.

2. Compactness: BLS signatures are compact, requiring minimal storage, making them ideal for resource-constrained environments.

3. Multisignature Support: BLS signatures enable efficient multisignature schemes, where multiple signatures can be aggregated into a single, compact signature.

Limitations:

1. Message Uniqueness: BLS signatures do not inherently enforce message uniqueness. If two different messages hash to the same point on the curve (a rare event), the same signature could be used for both.

2. Quantum Vulnerability: While BLS signatures are secure against classical attacks, they may be vulnerable to quantum attacks due to the reliance on bilinear pairings.

Applications:

1. Cryptocurrencies: BLS signatures are used in various cryptocurrencies, such as Ethereum 2.0 and Algorand, for secure transaction validation and key management.

2. Blockchain Consensus: In blockchain consensus protocols like PBFT and HotStuff, BLS signatures play a critical role in ensuring the correctness and efficiency of block propagation.

---

Introduction to BLS12-381

BLS12-381 is a popular elliptic curve used in modern cryptographic protocols, especially those requiring pairing-based operations. It is particularly favored for applications like zk-SNARKs, BLS signatures, and decentralized systems, including Ethereum 2.0.

Key Properties of BLS12-381:

1. Elliptic Curve Equation:

   • BLS12-381 is defined by the equation $y^2 = x^3 + 4$ over a prime field $F_p$.

2. Prime Field $F_p$:

   • The prime field is defined by a large prime number $p$, specifically $p = 2^{381} - 19$, chosen for both security and efficiency.

3. Embedding Degree:

   • The curve has an embedding degree of 12, which is crucial for efficient pairing operations used in cryptographic applications.

4. Twist Curve:

   • BLS12-381 includes a twist curve, which aids in efficient pairing calculations by mapping the curve over an extension field.

5. Security Level:

   • The curve offers 128-bit security, sufficient for most modern cryptographic applications.

BLS Signatures with BLS12-381

BLS12-381 is often used in implementing BLS signatures, which are valued for their efficiency and unique aggregation properties.

BLS Signature Scheme Overview:

1. Key Generation:

   • Generate a private key $sk$ and compute the public key $pk = sk \cdot G$, where $G$ is a generator on the curve.

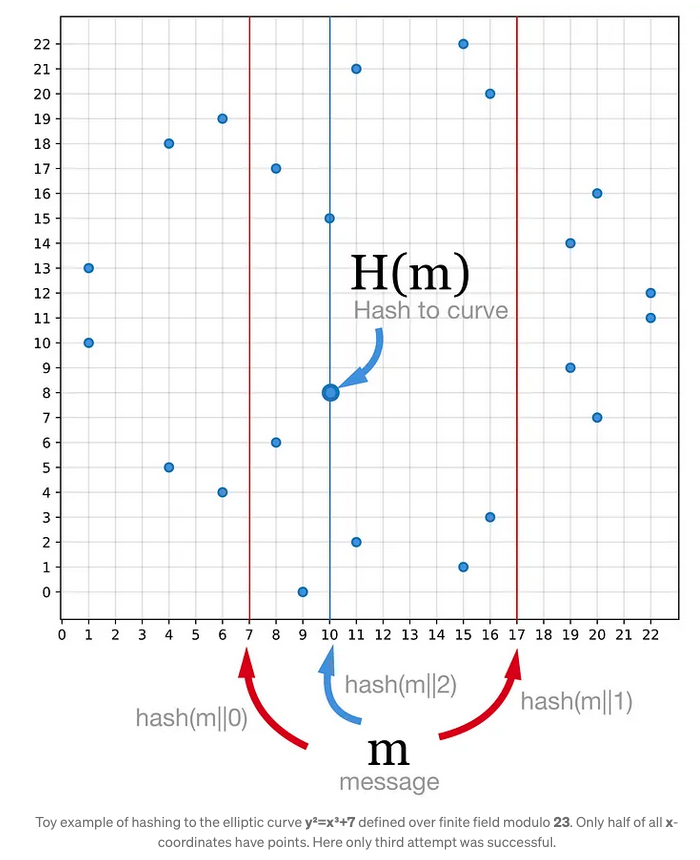
2. Signing:

   • Hash the message $m$ to a curve point $H(m)$.
   • Compute the signature $\sigma = sk \cdot H(m)$.
     
     https://medium.com/cryptoadvance/bls-signatures-better-than-schnorr-5a7fe30ea716

3. Verification:

   • Verify the signature by checking $e(\sigma, G) = e(H(m), pk)$.

   
   

Signature Aggregation

BLS signatures can be aggregated, allowing multiple signatures to be combined into one. For example, if multiple users sign different messages:

• $\sigma_1 = sk_1 \cdot H(m_1)$
• $\sigma_2 = sk_2 \cdot H(m_2)$
• $\sigma_3 = sk_3 \cdot H(m_3)$

The aggregate signature is:

$\sigma_{\text{agg}} = \sigma_1 + \sigma_2 + \sigma_3$

This can be verified against an aggregated public key:

$pk_{\text{agg}} = pk_1 + pk_2 + pk_3$

Background of this:
$e(P, Q + R) = e(P, Q) \cdot e(P, R)$
$e(pk,H(m))=e([sk]g_1,H(m))=e(g_1,H(m))^{(sk)}=e(g_1,[sk]H(m))=e(g_1,\sigma)$
$e([a]P,[b]Q)=e(P,[b]Q)^a=e(P,Q)^{ab}=e(P,[a]Q)^b=e([b]P,[a]Q)$
BLS12-381 for Rest of us

Pairings in BLS12-381

Pairing operations are central to the BLS signature verification process. In BLS12-381, a pairing function $e:G_1 \times G_2 \rightarrow G_T$ is computed between points on different groups, which enables efficient and secure signature verification.

Example with Concrete Values:

1. Private Key: $sk = 987654321$.
2. Public Key: $pk = sk \cdot G$.
3. Message: $m = \text{BLS example}$.
4. Hash: $H(m) = P$ (a specific point on the curve).

• Signature: $\sigma = 987654321 \cdot P$.
• Verification: Check $e(\sigma, G) = e(P, pk)$.

Summary

BLS12-381 is a robust elliptic curve used extensively in cryptographic applications, particularly for BLS signatures. The curve's design balances security, efficiency, and compatibility with pairing-based operations, making it suitable for secure communications and decentralized systems.

---

This version should be well-suited for your Velog blog with LaTeX support.