1. Symmetric vs Asymmetric Encryption (AES, RSA)

아래 내용은 내가 해당 주제를 공부하며 나름대로 정리한 내용이다. 이렇게 정리해 두면 추후에 복기하기가 매우 편리하다. 공부했지만 정리로 남기지 않은 내용도 꽤 있다. 따라서 각자 본인에게 맞는 방식으로 나름대로 정리해 보기를 추천한다.

Symmetric vs Asymmetric Encryption

Encryption algorithms can be broadly classified into two categories:
Symmetric and Asymmetric. The primary difference between them lies in
the way they use keys to encrypt and decrypt data.

Symmetric Encryption

In symmetric encryption, the same key is used for both encryption and
decryption. This means that anyone with access to the key can encrypt
and decrypt the data. Symmetric encryption is fast, efficient, and
widely used for bulk data encryption.

Example: Advanced Encryption Standard (AES)

• Key size: 128-bit, 192-bit, or 256-bit

• Block size: 128-bit

• Mode of operation: CBC, GCM, ECB, etc.

Youtube - Computerphile aes

Common Uses: AES is widely used for encrypting data at rest (e.g.,
files on a disk), encrypting data in transit (e.g., during secure
communication), and in various protocols like TLS (Transport Layer
Security).

AES is a popular symmetric-key block cipher that replaces DES (Data
Encryption Standard). It\'s widely used in various applications,
including secure web browsing (HTTPS), file transfers (SFTP), and
virtual private networks (VPNs).

AES 128 vs 192 vs 256

https://crypto.stackexchange.com/questions/20/what-are-the-practical-differences-between-256-bit-192-bit-and-128-bit-aes-enc

The larger key sizes exist mostly to satisfy some US military
regulations

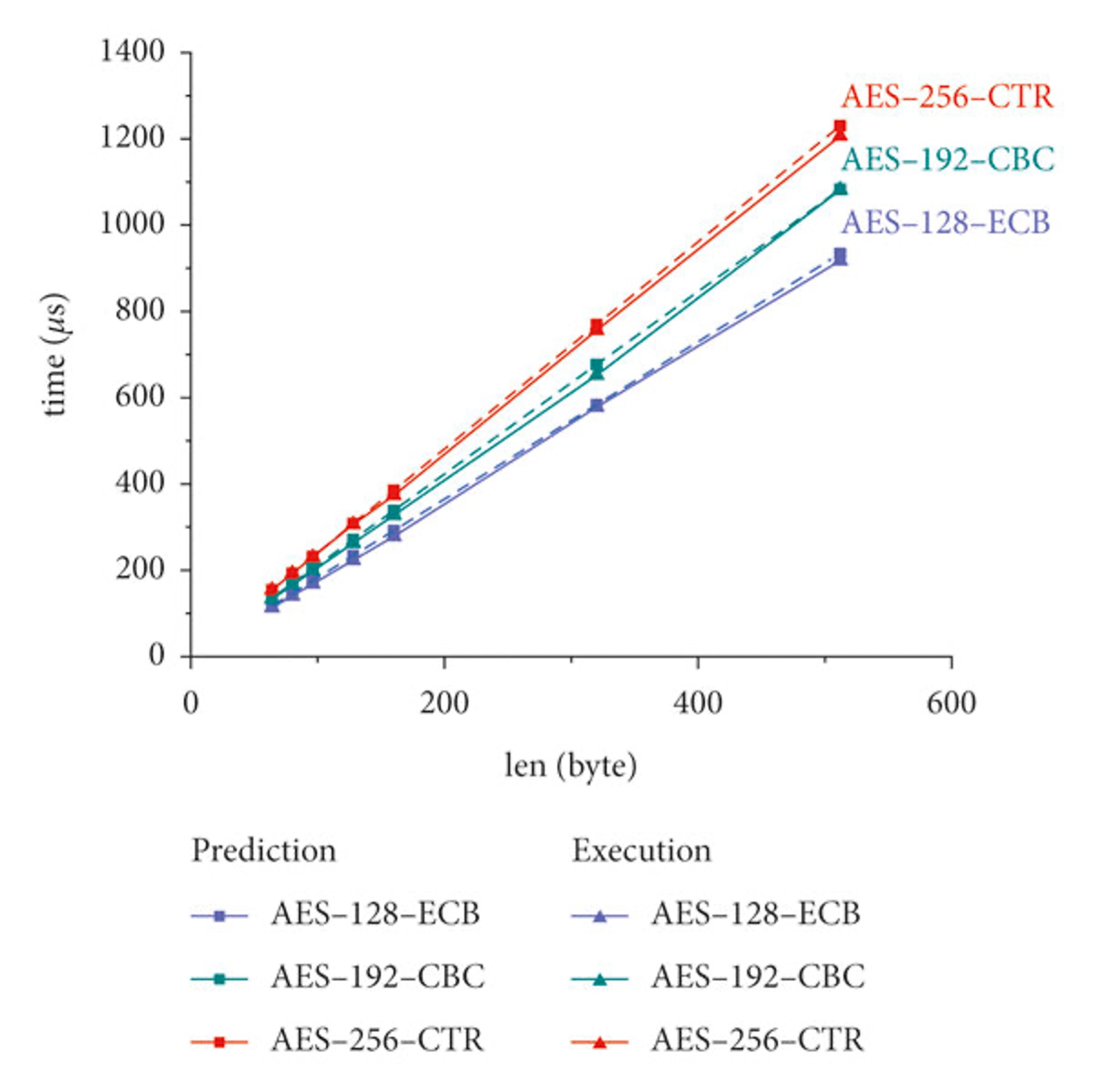
https://www.researchgate.net/figure/AES-encryption-with-variable-plaintext-length_fig4_357782653

Asymmetric Encryption

In asymmetric encryption, also known as public-key cryptography, a pair
of keys is used:

1. Public key: Used for encryption.

2. Private key: Used for decryption.

The public key can be shared openly without compromising security, while
the private key must remain secret. Asymmetric encryption is commonly
used for authentication, digital signatures, and establishing secure
connections.

Example: Rivest-Shamir-Adleman (RSA)

• Key size: Typically 2048-bit or larger

• Public exponent: Usually 65537

• Private exponent: Kept secret

Common Uses: RSA is often used for securing key exchanges (e.g., in
SSL/TLS handshakes), digital signatures (to verify the authenticity and
integrity of messages), and encrypting small amounts of data.

RSA is an asymmetric-key algorithm widely used for secure communication
over the internet. Its strength relies on the difficulty of factoring
large composite numbers. Common uses include SSL/TLS certificates, SSH
authentication, and email encryption.

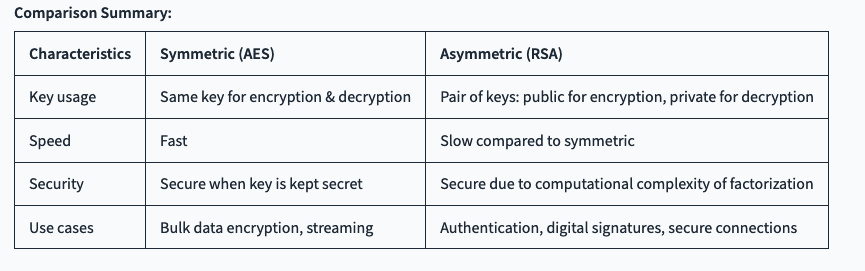
Comparison Summary:

When choosing between symmetric and asymmetric encryption, consider the
following factors:

1. Security requirements: If high-speed encryption is needed,
   symmetric encryption might be preferred. For authenticity and
   non-repudiation, asymmetric encryption is often chosen.

2. Key management: Managing pairs of keys can be more complex than
   handling single symmetric keys.

3. Computational resources: Asymmetric encryption requires more
   processing power due to its mathematical nature.

Keep in mind that many real-world cryptographic systems combine elements
of both symmetric and asymmetric encryption to leverage their strengths.
Examples include hybrid cryptosystems like PGP (Pretty Good Privacy) and
HTTPS (SSL/TLS).

N = p x q where p and q should be very far apart. Choose random numbers,
and find close prime numbers.

### Example

1. **Key Generation**:

- Select primes
$\text{(}\ p\ = \ 61\ \text{)}\ and\ \text{(}\ q\ = \ 53\ \text{)}.$

- Compute \$(\ n\ = \ pq\ = \ 61\ \times 53\ = \ 3233\ \text{)}.$

- Compute
$\text{(}\phi(n) = (p - 1)(q - 1) = 60 \times 52 = 3120\text{)}.$

- Choose
$\text{(}e = 17\text{)}(common\ choice\ and\ coprime\ with\ 3120).$

- Compute
$\text{(}d\text{)}such\ that\text{(}ed \equiv 1\ mod\ 3120\text{)}:$

$\text{[}d = 2753\text{]}\left( since\text{(}17 \times 2753 \equiv 1\ mod\ 3120 \right)$

Public key: $\text{(}(n,e) = (3233,17)\text{)}$

Private key: $\text{(}(n,d) = (3233,2753)\text{)}$

2. **Encryption**:

- Message $\text{(}\ M\ = \ 65\ \text{)}.$

- Compute ciphertext:

$\text{[}C = 65^{17}\ mod3233 = 2790\text{]}$

3. **Decryption**:

- Compute plaintext:

$\text{[}M = 2790^{2753}\ mod3233 = 65\text{]}$

### Security

The security of RSA is based on the difficulty of factoring the large
composite number $\text{(}\ n\ \text{)}$ into its prime factors
$\text{(}\ p\ \text{)}$ and $\text{(}\ q\ \text{)}.$ If an attacker can
factor $\text{(}\ n\ \text{)},$ they can compute
$\text{(}\phi(n)\text{)}$ and thus determine the private key
$\text{(}\ d\ \text{)}.$ The best-known algorithms for factoring large
integers, such as the General Number Field Sieve (GNFS), are not
efficient for sufficiently large $\text{(}\ n\ \text{)}$, making RSA
secure when proper key sizes are used (e.g., 2048 bits or larger).