NVP(1) - Paper Review

Stable Diffusion model에 이어, 3/10(금)에 교수님께서 새롭게 내주신 논문을 리뷰해보기로 한다.

---

Scalable Neural Video Representations with Learnable Positional Features (Subin, Sihyun, et al. NeurIPS 2022)

논문 코드: https://github.com/subin-kim-cv/NVP

Introduction

• CNR(Coordinate-based Neural Representations)은 gigapixel images, audios, 3D scenes, large city-scale street views와 같은 complex signal을 coordinate grid 상이 아닌 parameterized neural network 상에서 compact하게 저장하는 방식이다.
• 특히, 최근 CNR을 video signal에 접목하려는 시도가 이루어지고 있으며, 이는 $f(x,y,t)=(r,g,b)$ 형태의 neural network, 즉 임의의 time $t$에 대한 $(x,y)$ 좌표의 RGB pixel 값을 출력하는 함수를 학습시키는 것이다.
• 이는 복잡한 temporal dynamics와 커다란 spatial variation을 동시에 고려해줘야 하는 video의 특성상 어려움이 있는데, Chen et al.의 연구에서는 temporal dimension에 대해서만 modeling하는 방식으로 현존하는 video codec만큼의 성능을 이끌어내기도 하였다.
• 하지만 CNR의 가장 큰 한계점은 극심한 compute-inefficiency로, real world data에 적용하기 어려워진다.
• 이를 해결하기 위해 CNR을 1) coordinate-to-latent mapping $g_\theta(x,y,t)=z$ (latent grids $U_\theta\in R^{H\times W\times C}$로의 embedding function)와 2) latent-to-RGB mapping $h_\phi(z)=(r,g,b)$의 단계로 나누어 해결하려는 시도도 이루어졌는데, 이는 input dimension에 따라 너무 많은 parameter가 소요된다는 문제점이 있다.

Contribution

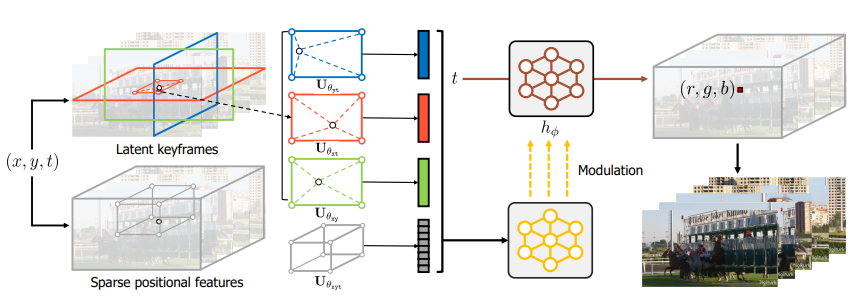
• 제안된 NVP(neural video representations with learnable positional features) 모델은 다음의 세 가지 contribution을 포함한다.

1. $g_\theta$의 $H\times W\times C$ size의 full-dimentional 3D array 대신 learnable positional features를 도입한다.
   $\text{ }\text{ }\Rarr g_\theta=g_{\theta_{xy}}\times g_{\theta_{xt}}\times g_{\theta_{yt}}\times g_{\theta_{xyt}}$, for $\theta:=(\theta_{xy},\theta_{xt},\theta_{yt},\theta_{xyt})$

   • Latent keyframes : $g_{\theta_{xy}},g_{\theta_{xt}},g_{\theta_{yt}}$는 각 spatio-temporal axis에 대해 video contents를 학습해 "image-like" 2D latent grid $U_{\theta_{xy}}, U_{\theta_{xt}}, U_{\theta_{yt}}$로 mapping한다.
   • Sparse positional features : $g_{\theta_{xyt}}$는 video pixel보다 작은 size로 local video detail을 학습해 "video-like" 3D latent grid $U_{\theta_{xyt}}$로 mapping한다.

2. 기존의 image & video codec(JPEG, HEVC)을 활용하여 parameter $\theta$의 개수를 줄였으며, 이는 trained parameter에 대해 re-training이 불필요하므로 compute-efficiency도 높인다.

   • 이는 기존의 hashing-based latent grid 방식에는 적용할 수 없다.

3. $h_\phi$에서, temporal coordinate에 대해 modulated network를 사용하여 encoding quality를 높였다.

---

Related Work

Coordinate-based Neural Representations (CNRs)

• 흔히 multilayer perceptron (MLP)가 high-frequency sinusoidal activation 혹은 Gaussian activation과 결합되어 있는 형태로, signal을 neural network로 encoding하는 방식을 일컫는다.
• Video encoding에 대한 연구가 진행되고 있으나, 아직 부족한 편이다.

Hybrid CNRs

• Coordinate-to-RGB mapping을 대신하여 그 사이에 grid structure를 따르는 latent code를 두는 방식을 일컫는다.
• Grid-shaped latent code는 video의 locality를 유지하여 좋은 성능을 보이지만, 필요한 parameter의 개수가 data resolution에 비례하여 증가한다.

---

NVP: Neural Video Representations with Learnable Positional Features

• Goal: 주어진 video signal $v:=(f_1, f_2, ... , f_T)$에 대해, compact neural representation $f_w$을 학습하는 것.

1. Architecture

• $w:=(\theta, \phi)\text{ }\text{ }$ ( $\theta:=(\theta_{xy},\theta_{xt},\theta_{yt},\theta_{xyt})$ )

• Coordinate-to-latent mapping $g_\theta$
  : $g_\theta=g_{\theta_{xy}}\times g_{\theta_{xt}}\times g_{\theta_{yt}}\times g_{\theta_{xyt}}$ with $g_\theta(x,y,t)=(z_{xy},z_{xt},z_{yt},z_{xyt})$

  a. Learnable latent keyframes $g_{\theta_{xy}}, g_{\theta_{xt}}, g_{\theta_{yt}}$

  • Image-like 2D latent spatial grid $U$는 $L$-level multi-resolution structure를 가지며( i.e. $U:=(U_1, ... , U_L)$ ), 각 spatial grid $U_l$은 $H_l=\lfloor\gamma^{l-1}H_1\rfloor$, $W_l=\lfloor\gamma^{l-1}W_1\rfloor$의 size를 가진다. (coarse to fine) $\Rarr$ $L=16, \gamma=1.35, H_1=W_1=16$
    $\rarr$$\text{ }U_l:=(u_{ij}^l)\in R^{H_l\times W_l\times C}$ for $l=1, ... , L$
    $\rarr$ 다양한 크기의 동일한 객체에 대한 학습을 기대.
  • 예를 들어, $U_{\theta_{xy}}$는 temporal axis에 대해 공통적인 특징들(ex. 배경, 워터마크 등)을 학습한다.
  • $U_l$의 각 좌표에 해당하는 latent code $u_{ij}^l$은 $C$-dimensional vector에 해당하며, latent vector $z_{yt}^l$은 가장 인접한 네 개의 latent code를 linearly interpolate한 값을 갖는다. (이 때, 주어진 $(y, t)$ 좌표에 대한 $H_l\times W_l$ grid의 relative position이 고려되며, 핵심은 latent code가 학습된다는 것과 across spatial axes에 대해서도 고려한다는 것.) $\Rarr$ $C=2$ and $4$ for NVP-S and NVP-L, respectively.
    

  b. Sparse positional features $g_{\theta_{xyt}}$

  • Video-like 3D latent spatial grid $U_{\theta_{xyt}}$는 실제 video의 3D RGB grid보다 훨씬 작은 $H\times W\times S$의 크기를 가진다.
    $\rarr$$\text{ }U_{\theta_{xyt}}:=(u_{ijk})\in R^{H\times W\times S\times D}$
    $\Rarr$ $300\times300\times300$ for ShakeNDry, $300\times300\times600$ for UVG-HD
  • $U_{\theta_{xyt}}$의 각 좌표에 해당하는 latent code $u_{ijk}$는 $D$-dimensional vector에 해당하며, latent vector $z_{xyt}$는 인접한 $h\times w\times s$개의 latent code를 concatenate하여 구해진다. ($h, w, s$는 hyperparameter에 해당한다.)
    $\rarr$ Sparse 3D grid 상의 latent code 하나만으로는 주어진 좌표에 대한 정보가 충분히 담기지 않아 여러 vector를 concatenate하였으며, linear interpolation은 computational cost가 증가하여 선택하지 않았다.
    $\Rarr$ $h=3, w=3, s=1,$ $D=2$ and $4$ for NVP-S and NVP-L, respectively.
  • 임의의 $(x,y,t)$ 좌표에 대한 RGB 값을 구하기 위해 network 상의 모든 parameter를 활용했던 기존의 CNR과는 달리, $U_{\theta_{xyt}}$의 locality를 활용하여 계산 효율을 높였다.

  정리하면, 아래의 표와 같다.

  	Latent keyframes $g_{\theta_{xy}}, g_{\theta_{xt}}, g_{\theta_{yt}}$	Sparse positional features $g_{\theta_{xyt}}$
  Grids	"Image-like" 2D latent grids $U_{\theta_{xy}},U_{\theta_{xt}},U_{\theta_{yt}}$ L-level multi-resolution structure $U:=(U_1,...,U_L)$	"Video-like" 3D latent grid $U_{\theta_{xyt}}$
  Latent codes	각 $U_l$ grid에 대해, $C$-dimentional vector $u_{ij}^l$이 $H_l\times W_l$만큼 존재	$D$-dimentional vector $u_{ijk}$가 $H\times W\times S$만큼 존재
  Latent vector	$z_{xy}^l,z_{xt}^l,z_{yt}^l$는 각각 가까운 네 개의 latent code $u_{mn}^l\text{'}s$를 linear interpolate한 값에 해당	$z_{xyt}$는 가까운 $h\times w\times s$개의 latent code를 concatenate한 값에 해당

• Latent-to-RGB mapping $h_\phi$
  : $h_\phi(z_{xy},z_{xt},z_{yt},z_{xyt})=(r,g,b)$

  • Latent vector $z$를 $(r,g,b)$ 값으로 mapping하는 과정에 Multi-Layer Perceptrion(MLP)을 적용하는 것이 일반적이지만, 동적인 video에 대해서는 expressive power가 떨어진다.
  • 따라서, $K$-layer MLP의 synthesizer network와 별도의 modulator network를 병렬적으로 두어 latent vector $z$와 time coordinate $t$를 각각 통과시키는 방법을 택하였다.
    $\Rarr$ K=3, |$z$|$=128$

  a. Modulated implicit function

  • Synthesizer($K$-layer MLP)는 $k$-1번째 layer에서 전달된 값을 변형하는 weights $A_k$와 bias $b_k$로 구성되어 있으며, sinusoidal activation을 사용한다.
  • 반면 modulator는 각 $k$번째 layer에 대한 hidden feature $z_k$로 구성되어 있으며, ReLU와 같은 piecewise linear activation(LeakyReLU)을 사용한다. 이를 수식과 그림으로 나타내면 아래와 같다.

    $\alpha_0=t$
    $\alpha_k=z_k\odot sin(A_k\alpha_{k-1}+b_k)$ for $k=1, ..., K-1$
    $(r,g,b)=A_K\alpha_{K-1}+b_K$

    

2. Compression procedure

• Parameter 수를 줄이기 위해 training 후 magnitude pruning이나 quantization 등을 접목한 기존의 아이디어는 CNR parameter에 대한 재학습이 수반되어 커다란 computational cost가 필요했다.
  • Magnitude pruning: 특정 값을 기준으로 weight 값을 thresholding하는 방법. 보통 학습 후 pruning을 진행한 sparse network에 대하여 학습을 다시 수행한다(iterative pruning).
• Coordinate-to-latent mapping $g_\theta$의 parameter를 줄이는 것이 핵심이며, 현존하는 image & video codec(HEVC, JPEG)을 활용해 latent spatial grids $U_{\theta_{xyt}},U_{\theta_{xy}},U_{\theta_{xt}},U_{\theta_{yt}}$를 8-bit latent code로 quantize하였다.

---

Experiments

• UVG-HD의 7개 video에 대해 성능을 측정(각 frame에 대한 값을 전체 video에 대해 평균)하여 평균내었으며, metric으로는 PSNR, LPIPS, FLIP, SSIM을 사용하였다.
• Encoded video와 원본 간의 perceptual similarity를 측정하는 LPIPS 수치를 크게 향상시켰으며 모델의 robustness에 해당하는 variance 값도 작았다.
• Applications: Video inpainting, video frame interpolation, video super-resolution, video compression에 좋은 성능을 보였다.
• Sparse positional features $U_{\theta_{xyt}}$는 latent code 간의 non-smooth transition을 완화시키고, video의 sharp detail을 학습하는 것으로 해석하였다. 또한, $U_{\theta_{xyt}}$ 상에서 linear interpolation을 적용하면 더 smooth한 pattern을 보이지만, 학습시간이 1.61배 소요되었다.

---

Discussion and Conclusion

• Video의 특성에 맞게 architecture나 hyperparameter를 변형하면 더 좋은 성능을 기대해볼 수 있을 것이다.

---

Appendix

Baseline methods

• SIREN: High frequency sine activation을 적용해 $(x,y,t)\rarr(R,G,B)$로 mapping하는 모델.
• FFN: Random fourier feature를 활용하여 positional embedding layer를 구성하고, ReLU activation을 적용한 모델.
• NeRV: Video에 특화된 CNR 모델로, time index를 입력받아 그에 해당하는 RGB image를 출력.
• Instant-ngp: Trainable feature vector로 구성된 multiresolution hash table을 활용하는 모델.

---

추가로 고민해봐야 할 것

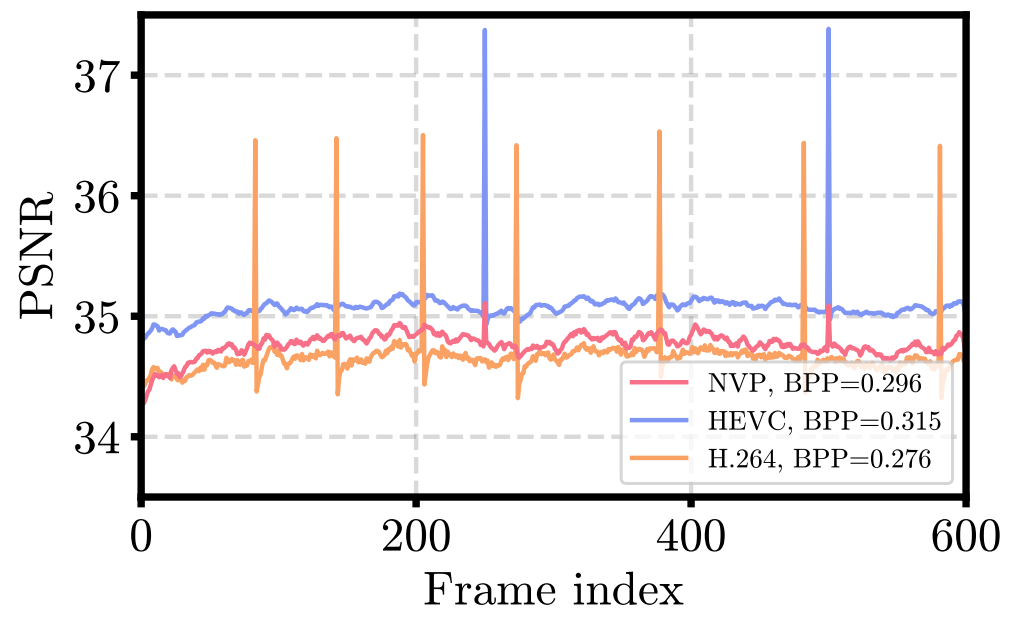
$\Rarr$ NVR 모델은 압축에 특화되어 있지는 않기 때문에 현존하는 다른 video codec에 비해선 다소 떨어지는 reconstruction 성능을 보여준다. 압축에 특화되도록 아이디어를 발전시켜 본다면?