NVP2(4) - Tucker Decomposition

구명규·2023년 4월 17일

'23 Individual Research

목록 보기

14/19

Codec에 이어, sparse grid에 적용해보기로 한 Tucker decomposition에 관해서도 공부하여 정리해보도록 하겠다.

Tensor Decomposition

먼저 $m\times n$ 의 2차원 matrix를 생각해보자. 이는 각각 $m$ , $n$ 차원의 1차원 vector의 곱으로 나타내어질 수 있다. 정확히는, 정보량 차이로 인해 matrix와 최대한 유사해지도록 두 vector를 학습시킬 수 있으며, 남은 오차는 또 다른 두 쌍의 vector를 추가하며 줄여나갈 수 있다. 이처럼 한 matrix를 표현하기 위해 사용된 vector의 곱셈 단위를 Rank라고 하며, 이를 그대로 tensor에 적용하여 임의의 tensor를 r개의 Rank로 분해하는 것을 r Rank Tensor Decomposition이라고 한다. 이 때 rank $r$ 은 hyperparameter에 속한다.

이러한 tensor decomposition은 독립적인 factor들의 합으로 구성되는 1)CP-Decomposition과 core tensor를 통해 factor간 상관관계를 고려하는 2)Tucker Decomposition으로 나뉜다.

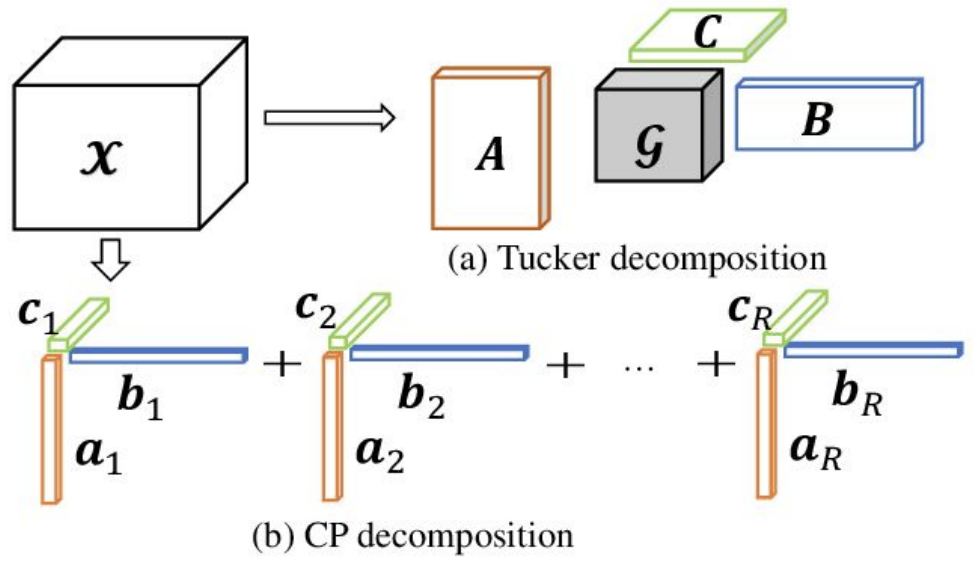
CP-Decomposition

CP-decomposition에서 사용되는 objective function은 다음과 같다.

\|\chi-\sum_{r=1}^Ra_r\circ b_r \circ c_r\|

앞서 설명한 분해 방식과 그대로 일치하며, $n_1\times n_2\times n_3$ 크기의 3차원 tensor를 $n_1$ 크기의 vector( $a_r$ ) $R$ 개, $n_2$ 크기의 vector( $b_r$ ) $R$ 개, $n_3$ 크기의 vector( $c_r$ ) $R$ 개로 표현하게 된다. 여기서 $n_i$ 크기의 vector $R$ 개를 $n_i\times R$ 크기의 2차원 matrix라고 생각한다면, 아래와 같이 분해하는 것이 CP-decomposition이라 할 수 있겠다.

$n_1\times n_2\times n_3$ tensor
$\text{ }\Rarr\text{ }$ $n_1\times R$ , $n_2\times R$ , $n_3\times R$ projection matrices

Tucker Decomposition

한편, Tucker decomposition의 경우 다음과 같은 objective function을 사용한다.

\|\chi-\sum_{r_1=1}^{R_1}\sum_{r_2=1}^{R_2}\sum_{r_3=1}^{R_3}g_{r_1r_2r_3}a_{r_1}\circ b_{r_2}\circ c_{r_3}\|

즉, $n_1\times n_2\times n_3$ 크기의 3차원 tensor를 $n_1$ 크기의 vector( $a_r$ ) $R_1$ 개, $n_2$ 크기의 vector( $b_r$ ) $R_2$ 개, $n_3$ 크기의 vector( $c_r$ ) $R_3$ 개와 이들의 coefficient matrix 역할을 하는 $R_1\times R_2\times R_3$ 크기의 3차원 tensor(Core Tensor)로 표현하는 것이다. 이는 2차원 matrix에 대한 SVD decomposition의 차원 확장으로 여겨질 수 있다.

CP-decomposition에선 각각 $R$ 개의 vector들을 같은 index를 갖는 vector끼리만 외적하여 그대로 더하는 반면, Tucker decomposition에서는 각각 $R_1, R_2, R_3$ 개의 vector들을 그들의 모든 조합에 대해 외적한 후 그 조합에 해당하는 coefficient 값을 곱하여 표현하는 것이다. 이 때 $R_1, R_2, R_3$ 개의 coefficient core tensor에 담기게 된다.

앞선 CP-decomposition에서와 마찬가지로, vector들을 하나의 2차원 matrix로 표현하면 Tucker decomposition은 아래와 같은 형태의 분해 방식이라고 볼 수 있다.

$n_1\times n_2\times n_3$ tensor
$\text{ }\Rarr\text{ }$ $R_1\times R_2\times R_3$ tensor + $n_1\times R_1$ , $n_2\times R_2$ , $n_3\times R_3$ projection matrices

Comparison

앞선 두 decomposition 방식을 비교하자면, CP-decomposition의 경우 연산이 빠르나 근사하는 정보량이 적은 반면, Tucker decomposition은 연산이 느리나 근사하는 정보량이 많다는 이점을 지닌다.

Utilization in DL

이러한 decomposition 기법은 deep learning 분야에서 over parameterized model의 성능을 크게 떨어뜨리지 않으며 용량을 축소시키는 데 유용히 활용되고 있다.

우선 fully connected layer의 경우, 아래와 같은 matrix 연산으로 여길 수 있다.

Ax+b \text{ (A:weight matrix, b: bias matrix)}

따라서 SVD와 같은 matrix decomposition을 $A$ matrix에 적용하여 parameter의 수를 줄일 수 있다.

한편, 2D convolutional layer는 아래와 같은 3차원 tensor에 해당한다.

\text{ cols }\times\text{ rows }\times\text{ input\_channels }\times\text{ output\_channels }

이에 대해선 SVD를 3차원 tensor에 대해 확장한 Tucker decomposition을 적용하여 parameter의 수를 줄여줄 수 있는 것이다.

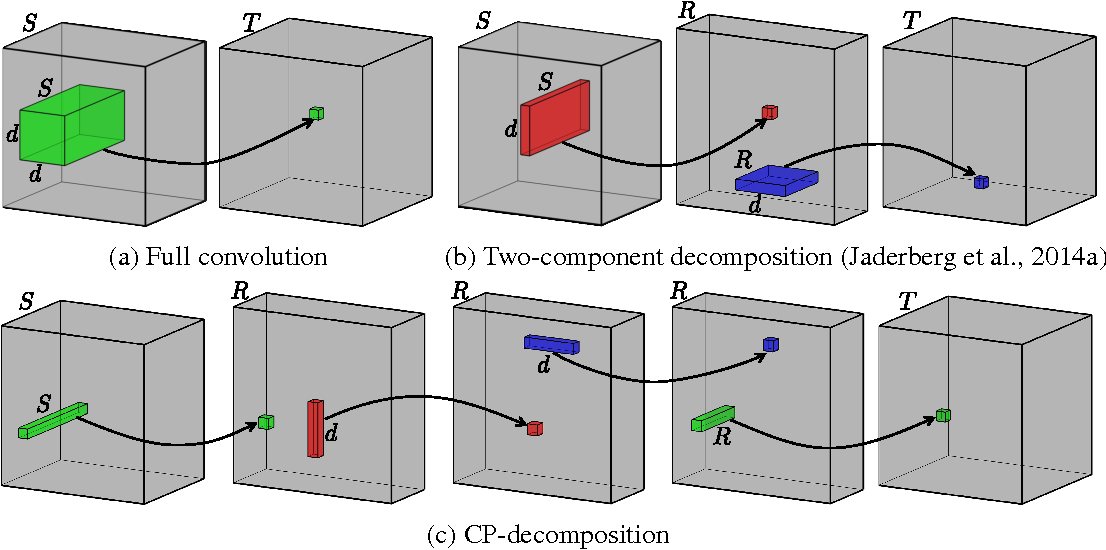
NVP 모델의 sparse positional features를 Tucker decomposition을 통해 1개의 축소된 3차원 tensor와 3개의 2차원 matrix로 압축한 뒤, 그 자체가 성능에 미치는 영향을 알아보고, decomposition의 결과물들에 각각 codec을 적용해보기도 할 예정이다. (물론 CP-decomposition에 대해서도 실험해볼 계획이다)

References

구명규

K'AI'ST 학부생까지의 기록

이전 포스트

NVP2(3) - Codec Basics

다음 포스트