DTW란?

시계열 분석에서 DTW(Dynamic Time Warping)는 속도가 다를 수 있는 시간적 시퀀스 간의 유사성을 측정하는 알고리즘이다. DP알고리즘의 특수한 케이스라고도 볼 수 있다.

필요성

대표적으로 시계열 간 유사도를 측정하는 방법은 유클리디안 거리가 있다. 하지만 비슷한 패턴임에도 불구하고 time shift가 있으면 전혀 다른 패턴으로 측정된다. DTW를 사용하면 이를 감안하여 패턴의 유사성을 측정할 수 있다. 시간이 warping되는(뒤틀리는) 구간을 찾고 이것이 최소가 되는 최적 경로를 찾아 그 거리를 계산한다. 계산된 거리가 작을수록 두 시계열은 유사하며 shifting도 작다는 의미이다.

DTW는 음성 인식, 동작 분석, 생체 신호 처리(예: ECG) 등에서 패턴 유사성 분석에 많이 사용된다.

1차원 시퀀스로 변환할 수 있는 모든 데이터에 대해 DTW로 분석할 수 있다.

제약 조건

대개 DTW는 두 시계열 간의 매칭을 정의하는 핵심 제약 조건 3가지을 사용해 두 개의 주어진 시퀀스 간의 최적 일치(Optimal Matching)를 계산한다.

1. boundary condition
   1. 첫 번째 시계열의 시작점은 반드시 두 번째 시계열의 시간점과 매칭되어야 한다.
   2. 첫 번째 시계열의 끝점은 반드시 두 번째 시계열의 끝점과 매칭되어야 한다.
   3. 즉, warping path는 반드시 시계열의 처음과 끝을 포함해야 한다.
2. continuity
   1. 매칭 경로는 시계열의 모든 인덱스를 연속적으로 따라가야 한다.
   2. 즉, i번째와 i+1번째 시점 간 인덱스 변화는 최대 1씩만 가능하다.
   3. 즉, 인덱스 변화는 한 번에 1씩만 이뤄져야 한다. 이는 경로가 시간적으로 비약하지 않도록 보장한다.
3. monotonicity
   1. 매칭 경로는 항상 시간적으로 앞으로 나아가야 한다.
   2. 즉, 한 시계열에서 나중 시점은 다른 시계열에서도 나중 시점과만 매칭될 수 있다.
   3. 이는 매칭 경로가 역방향으로 되돌아가거나 엉뚱한 방향으로 가지 않도록 보장한다.

이 규칙들을 만족시키면서, DTW는 두 시계열 간의 최적의 warping path를 찾아낸다. 이를 통해 시간 축의 왜곡을 허용하면서 시계열 간 유사성을 효과적으로 측정할 수 있게 된다.

코드

코드는 다음과 같다.

import matplotlib.pyplot as plt
import numpy as np

def dtw_distance(x, y, dist):
    m = len(x)
    n = len(y)
    
    # DTW 행렬 초기화
    dtw = np.zeros((m+1, n+1))
    # 첫 번째 행 초기화 (경로 시 제외하기 위해)
    dtw[0, 1:] = np.inf
    # 첫 번째 열 초기화 (경로 시 제외하기 위해)
    dtw[1:, 0] = np.inf
    # 후추 히트맵 시각화를 위한 행렬: 인접한 두 시점 간의 와핑 비용 행렬.
    heatmap = dtw[1:,1:].copy()
    
    # DTW 행렬 계산
    for i in range(1, m+1):
        for j in range(1, n+1):
            cost = dist(x[i-1], y[j-1])  # 두 데이터 포인트 간의 거리 또는 유사성 계산
            # dtw 최적 거리 누적 : DP알고리즘을 떠올리면 동일함을 알 수 있다!
            dtw[i, j] = cost + min(dtw[i-1, j], dtw[i, j-1], dtw[i-1, j-1])
            heatmap[i-1,j-1] = cost # 인접한 두 시점 간의 와핑 비용 저장
    
    # 시각화를 위한 최소 경로 리스트(최소 경로일 때의 누적 dtw거리 리스트)
    path = []
    while (m, n) != (1, 1):
        path.append((m, n))
        m, n = min((m - 1, n), (m, n - 1), (m - 1, n - 1), key=lambda x: dtw[x[0], x[1]])
    path.append((1,1))
    
    return dtw, heatmap, path, dtw[-1, -1]

def distance(a, b):
    return abs(a - b)

예시로 데이터를 만들어 계산해보자!

x = [1, 2, 5, 7, 4, 3, 6, 8, 2, 1]
y = [3, 6, 1, 2, 8, 9, 3, 4, 3, 2, 1, 2]

cost, heatmap, path, dtw_distance = dtw_distance(x, y, distance)

print("DTW 거리:", dtw_distance)

코드를 실행하면 결과는 다음과 같다.

DTW 거리: 17.0

와핑거리 누적 행렬과 와핑이 적용된 두 시퀀스의 관계에 대해서 다음의 코드로 알아볼 수 있다.

print(cost)
print('Total Distance is ', dtw_distance)

offset = 15 # 유연한 시각화를 위한 offset값

plt.xlim([-1, max(len(x), len(y)) + 1])
plt.plot(x)
plt.plot([i + offset for i in y])

for (i, j) in path:
    plt.plot([i-1, j-1], [x[i-1], y[j-1] + offset])

plt.show()

위 코드를 실행하면 결과는 다음과 같다.

[[ 0. inf inf inf inf inf inf inf inf inf inf inf inf]
 [inf  2.  7.  7.  8. 15. 23. 25. 28. 30. 31. 31. 32.]
 [inf  3.  6.  7.  7. 13. 20. 21. 23. 24. 24. 25. 25.]
 [inf  5.  4.  8. 10. 10. 14. 16. 17. 19. 22. 26. 28.]
 [inf  9.  5. 10. 13. 11. 12. 16. 19. 21. 24. 28. 31.]
 [inf 10.  7.  8. 10. 14. 16. 13. 13. 14. 16. 19. 21.]
 [inf 10. 10.  9.  9. 14. 20. 13. 14. 13. 14. 16. 17.]
 [inf 13. 10. 14. 13. 11. 14. 16. 15. 16. 17. 19. 20.]
 [inf 18. 12. 17. 19. 11. 12. 17. 19. 20. 22. 24. 25.]
 [inf 19. 16. 13. 13. 17. 18. 13. 15. 16. 16. 17. 17.]
 [inf 21. 21. 13. 14. 20. 25. 15. 16. 17. 17. 16. 17.]]
Total Distance is  17.0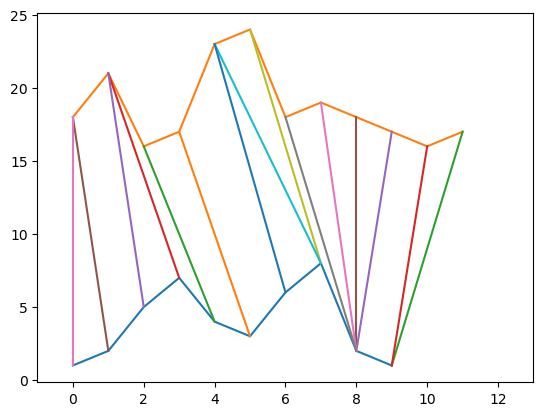

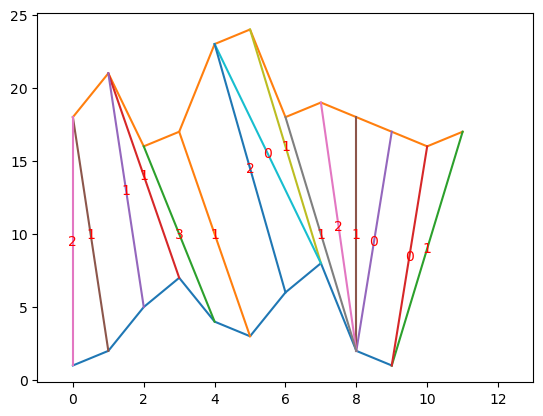
와핑 비용을 명시하면 다음과 같이 시각화할 수 있다. 명시된 숫자를 합하면 17이다.

각 위치에서 다음 경로까지 가는 거리 비용에 대한 히트맵을 시각화 하면 다음과 같다.

x_path = [p[0]-1 for p in path]
y_path = [p[1]-1 for p in path]
plt.imshow(heatmap.T, origin='lower', cmap=plt.cm.Reds, interpolation='nearest')
plt.plot(x_path, y_path, '-o')
plt.xticks(range(len(x)), x)
plt.yticks(range(len(y)), y)
plt.xlabel('x')
plt.ylabel('y')
plt.axis('tight')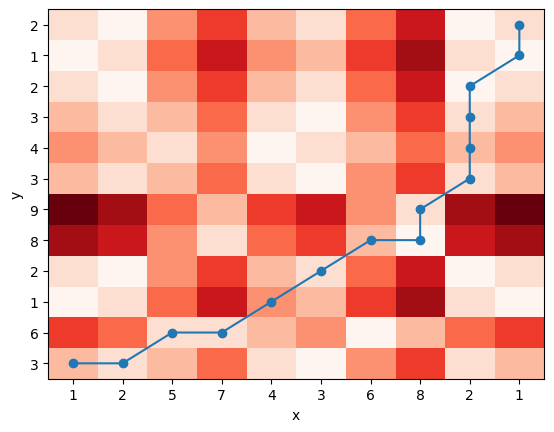

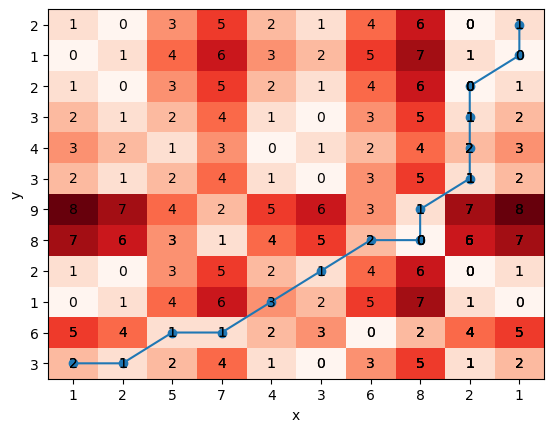
좀 더 알아보기 쉽게 경로 비용을 추가하면 다음과 같다. 지나간 칸의 수를 모두 합하면 17이다.

---

참고링크

• https://github.com/pollen-robotics/dtw/blob/master/dtw/dtw.py
• https://devhwi.tistory.com/28
• https://aliencoder.tistory.com/33