부동 소수점에 대해 공부하게되어 숫자 예시로 정리를 해보려고 한다.

컴퓨터는 숫자를 이진법으로 나타낸다.
십진법도 무한소수가 있듯이, 이진법에서도 유한한 bit로 나타낼 수 없는 숫자들이 있다.

물론 37.25처럼 이진법으로도 딱 떨어지는 숫자가 있을 수 있다.
예를 들어

37.25 = 32 + 4 + 1 + 0.25 = 2^5 + 2^2 + 2^0 + 2^-2

하지만 유한한 bit로 나타낼 수 없는 숫자의 예시도 있다.
대표적으로 0.1을 이진법으로 나타내면 어떻게 되는지 살펴보자.

0.1 ≈ 1/(2^4) + 1/(2^5) + 1/(2^8).....

딱 떨어지지 않는 무한 소수가 된다.

이렇게 소수 표현 시 이진법이기 때문에 필연적으로 오차가 발생하는 점을 감안하되, 소수를 나타낼 수 있는 대표적인 방식이 2가지가 있다.

고정 소수점

숫자 하나를 나타내기 위해 32개의 bit가 주어진다.
맨 앞의 비트는 양수인지 음수인지 부호를 나타낸다고 하면,
정수부와 소수부로 적당히 쪼개서 나머지 31개의 bit로 숫자를 표현할 수 있다.
고정 소수점 방식에서는 앞의 15개의 bit로는 정수를 나타내고, 뒤에 16개의 비트로는 소수점 뒷부분을 나타낸다.

그럼 정수부만 놓고볼 때 나타낼 수 있는 최대값은 2^15 - 1, 최소값은 -2^15이다.
만약 소수점을 별로 사용할 일이 없는 케이스라면 굉장히 비효율적일 것이다.
그렇다고 소수부를 줄이자니 소수점을 많이 사용해야 하면 어캄?

그래서 훨씬 더 넓은 범위의 숫자를 나타내기 위해 표준으로 정해진 것이 다음에서 설명할 부동 소수점 방식이다.

부동 소수점

부동 소수점 방식에서도 맨 앞의 비트는 부호를 나타낸다는 점은 동일하다.
아래와 같이 나타낼 수 있다.

1.(가수부)*2^(지수부 - 127)

예를 들어 34.125를 부동소수점 방식으로 나타내보자.

34.125를 이진수로 나타내면

34.125 = 32 + 2 + 0.625 = 2^5 + 2^1 + 2^-3
= 100010.001

이것을 1.xxxx의 형식으로 1과 유효숫자로 나타내보자.

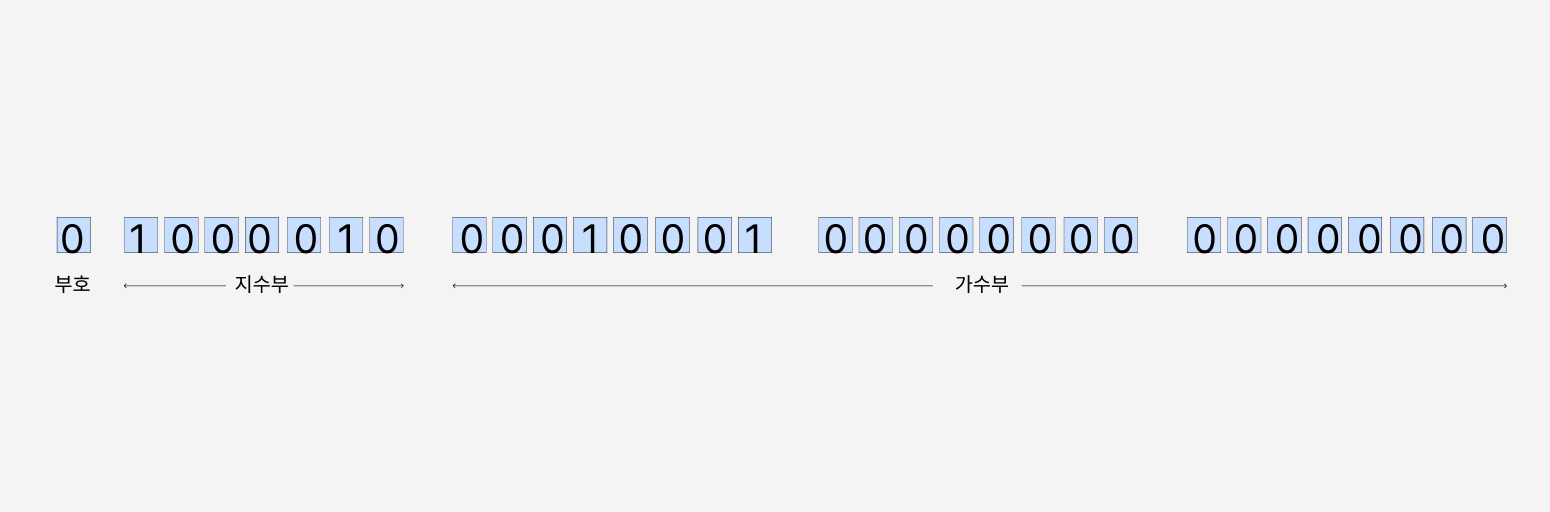
100010.001 = 1.00010001 * 2 ^ 3 = 1.00010001 * 2 ^ (130 - 127)

따라서 가수부의 앞부분은 00010001이고, 뒷부분은 모두 0으로 채운다. 지수부는 130을 이진수로 나타낸 10000010이다.

결과적으로 32bit로 나타내면

0 1000001 00001000 10000000 00000000

이러한 방식을 IEEE 754 단정밀도 방식이라고 한다.

참고:
얄팍한 코딩사전