1. 개요

각 노드의 자녀 수가 최대 2개인 트리 (트리의 차수 = 2)
자녀 노드를 left child와 right child로 나눌 수 있게 된다.

2. 형태에 따른 이진 트리 종류

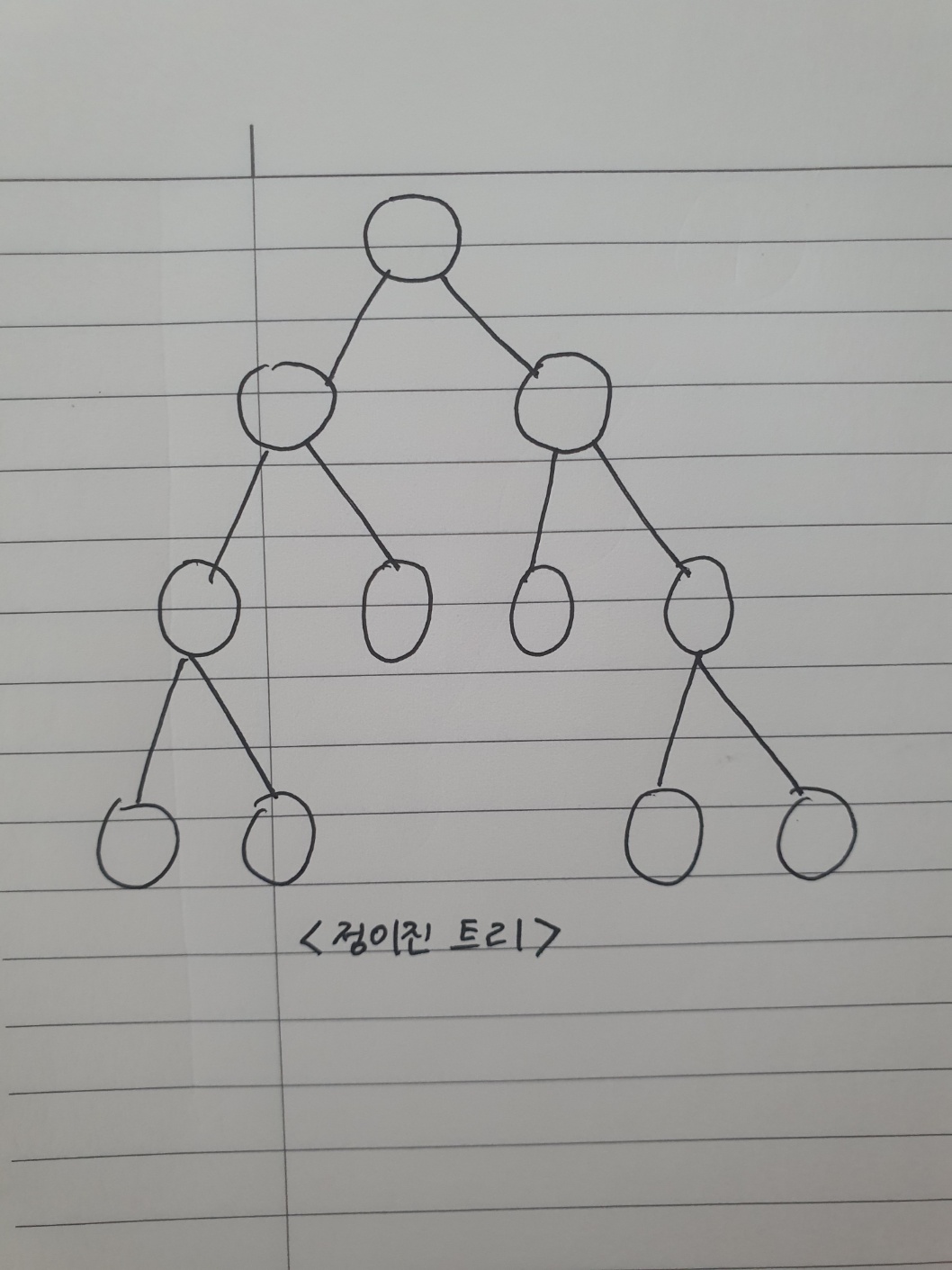
1) 정이진 트리(full binary tree)

: 모든 노드가 0개 또는 2개의 자식 노드를 가짐. (즉 자녀노드가 1개인 경우가 없음.)

최대 노드 개수 (h는 높이를 의미, 첫 항 = 2^0, 공비 = 2, 마지막 항 = 2^h):

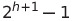
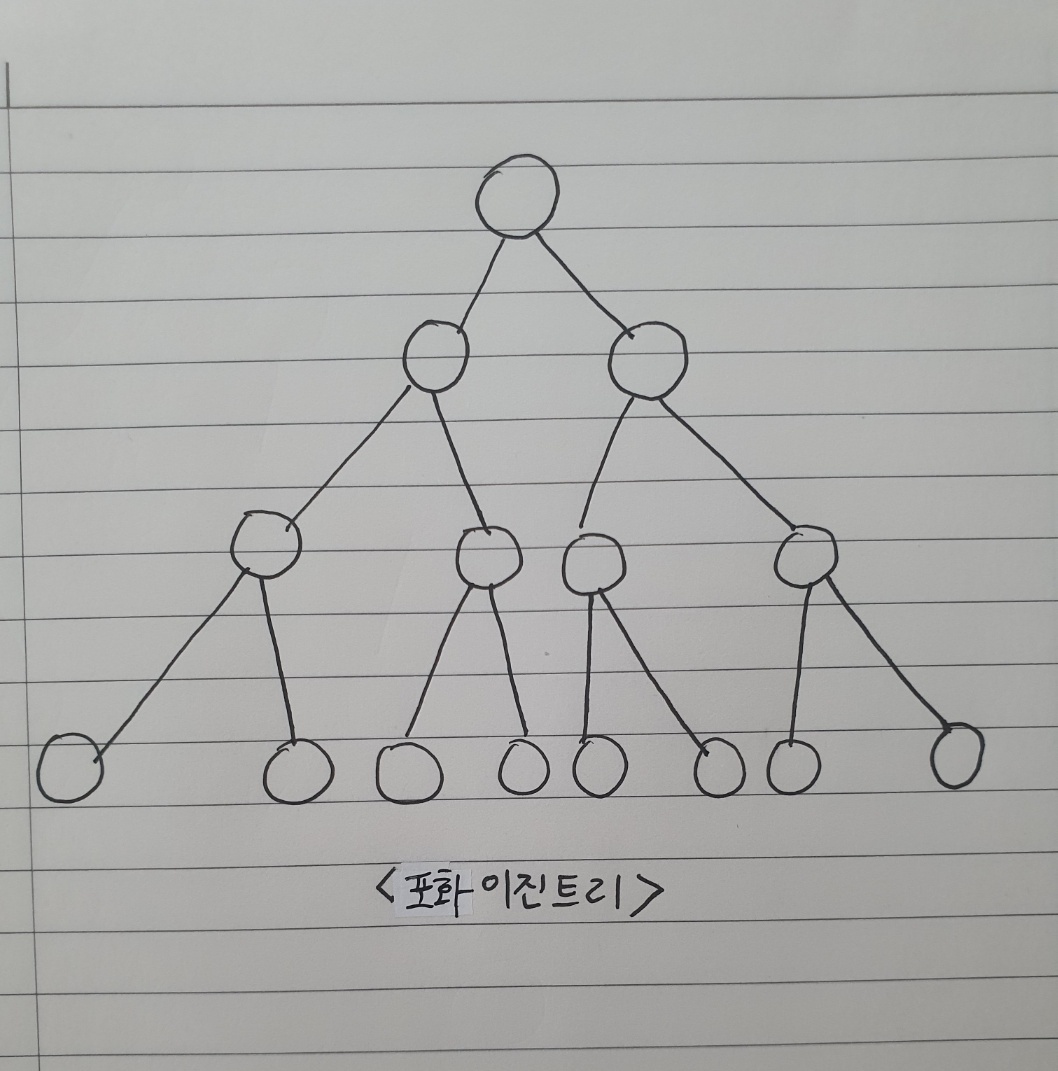
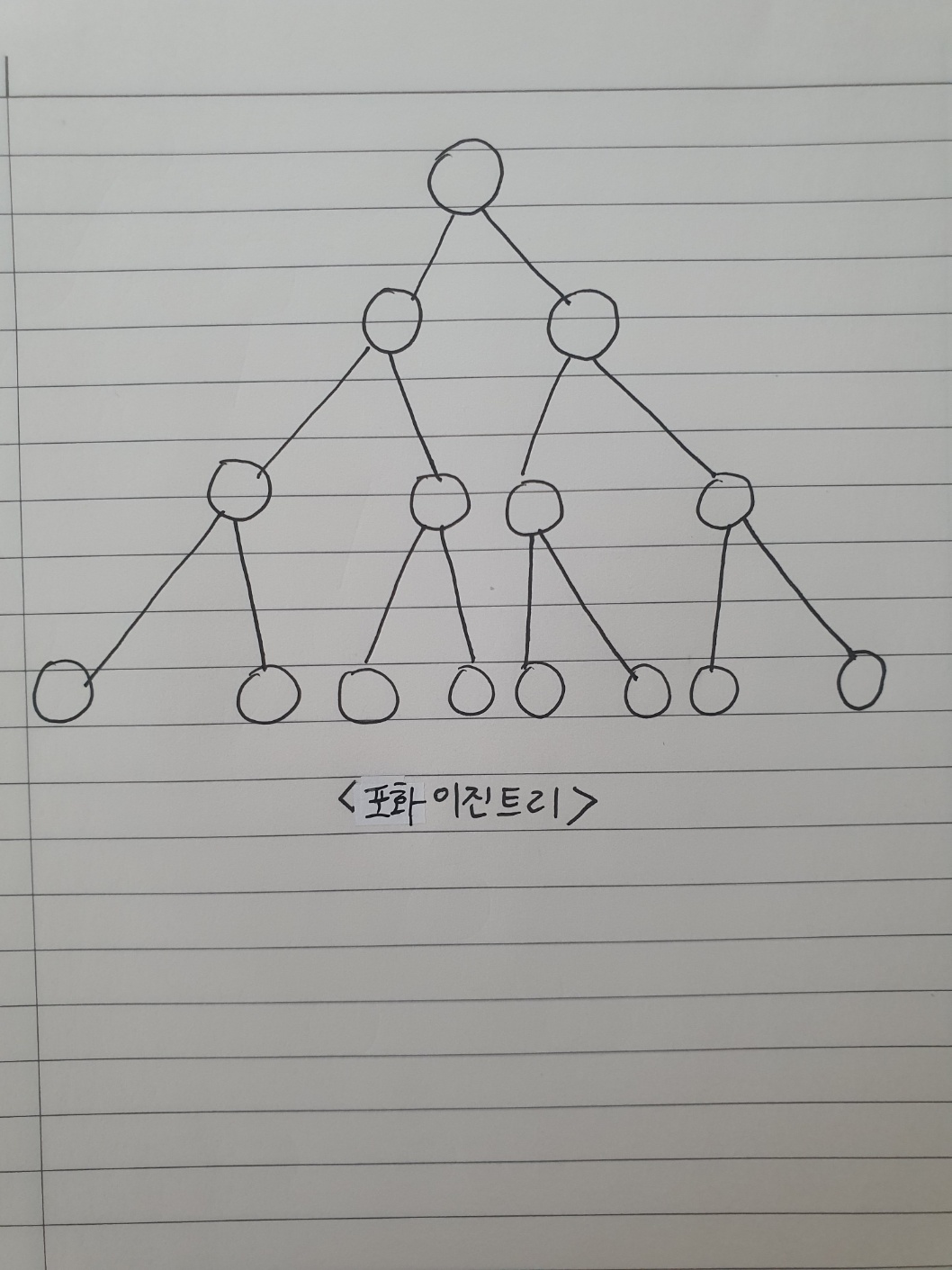
2) 포화 이진 트리(perfect binary tree)

: 모든 내부 노드가 2개의 자식노드를 가지고, 모든 잎 노드가 동일한 깊이를 가짐.

노드 개수 (h는 높이를 의미):

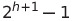
리프 노드 개수(l은 리프노드 개수를 의미, n은 node 개수를 의미):

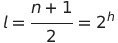
3) 완전 이진 트리(complete binary tree)

: 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 경우에는 왼쪽부터 채워져 있음. (오른쪽 리프 노드들이 탈모 마냥 없음)

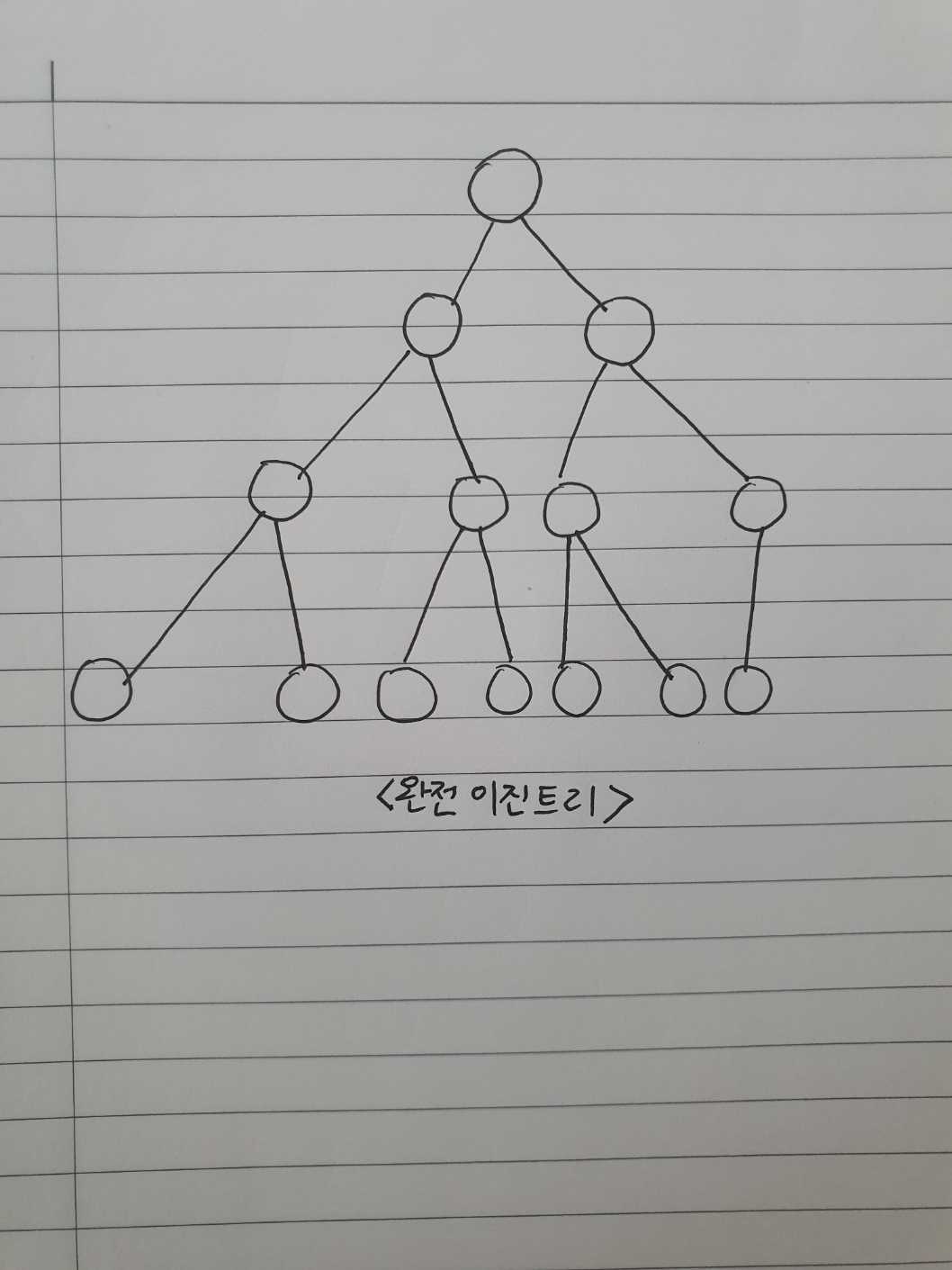
최대 노드 개수 (h는 높이를 의미):

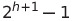
4) 균형 이진 트리(balanced binary tree)

: '모든 노드'에서 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1 이하.

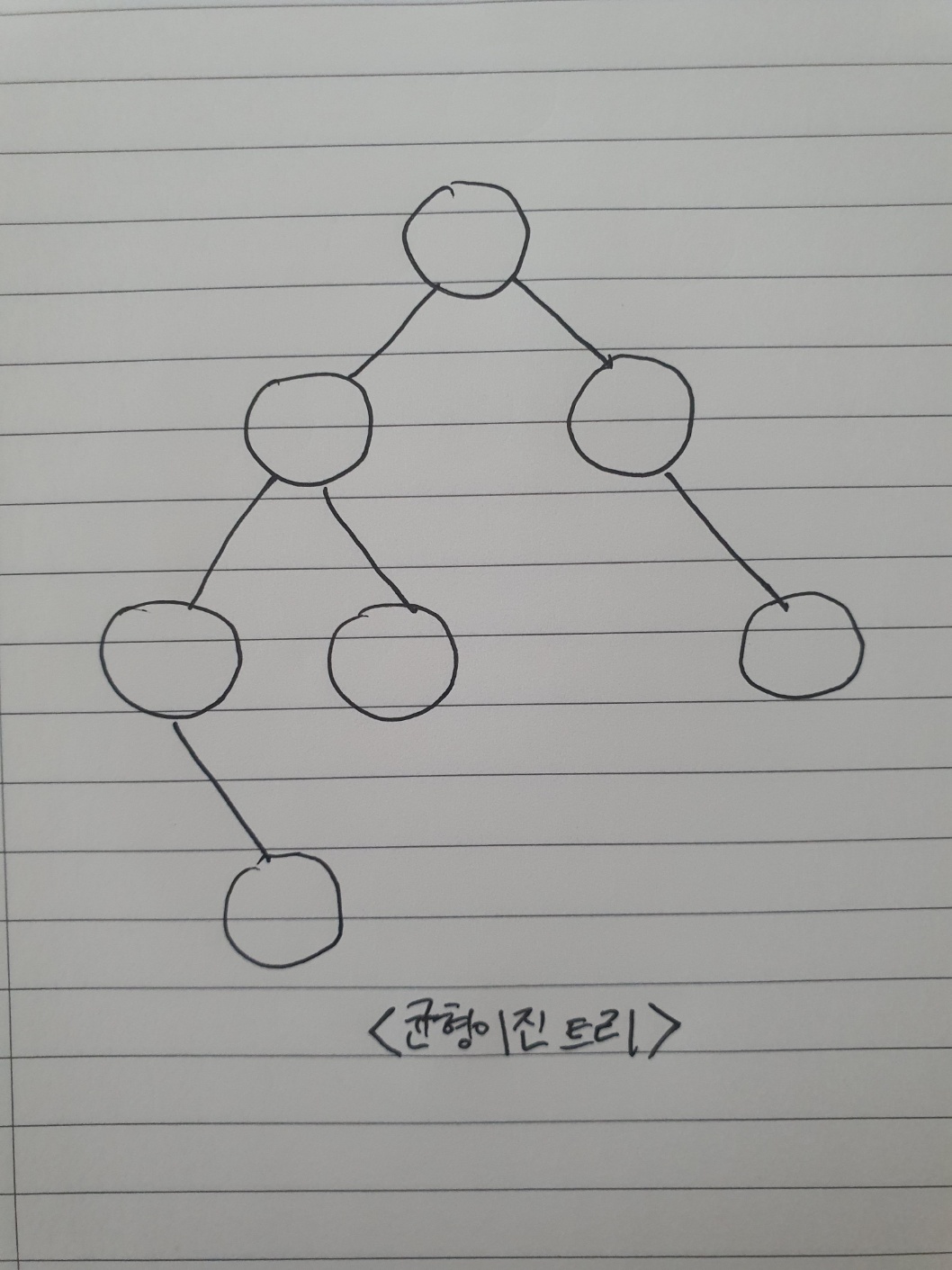
이후에 배우게 될 레드 블랙 트리는 균형 이진 트리 중 하나이다!

5) 변질 이진 트리(degenerate binary tree 또는 pathological binary tree)

: 각 부모 노드의 자식 노드가 하나밖에 없는 이진 트리

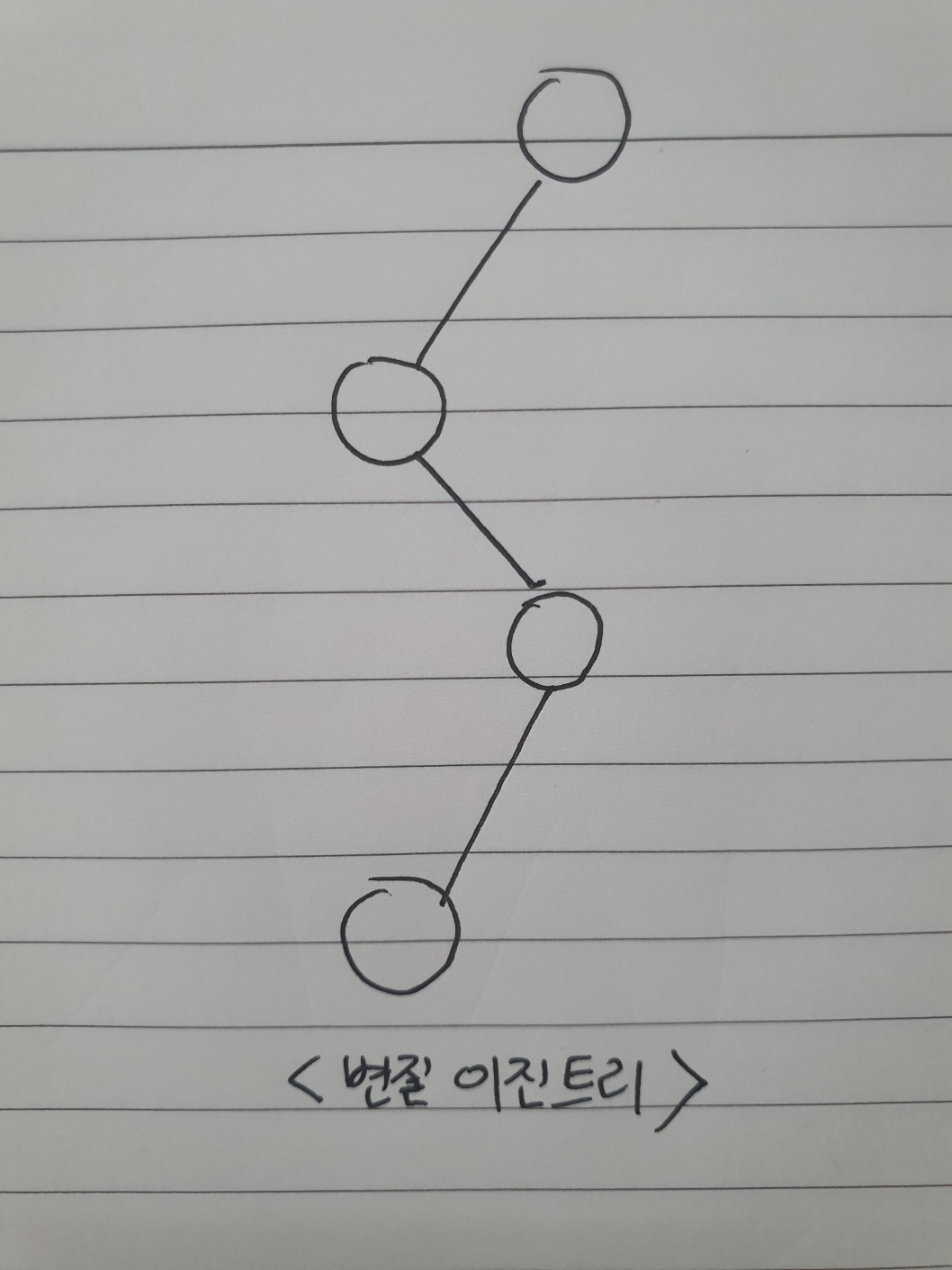
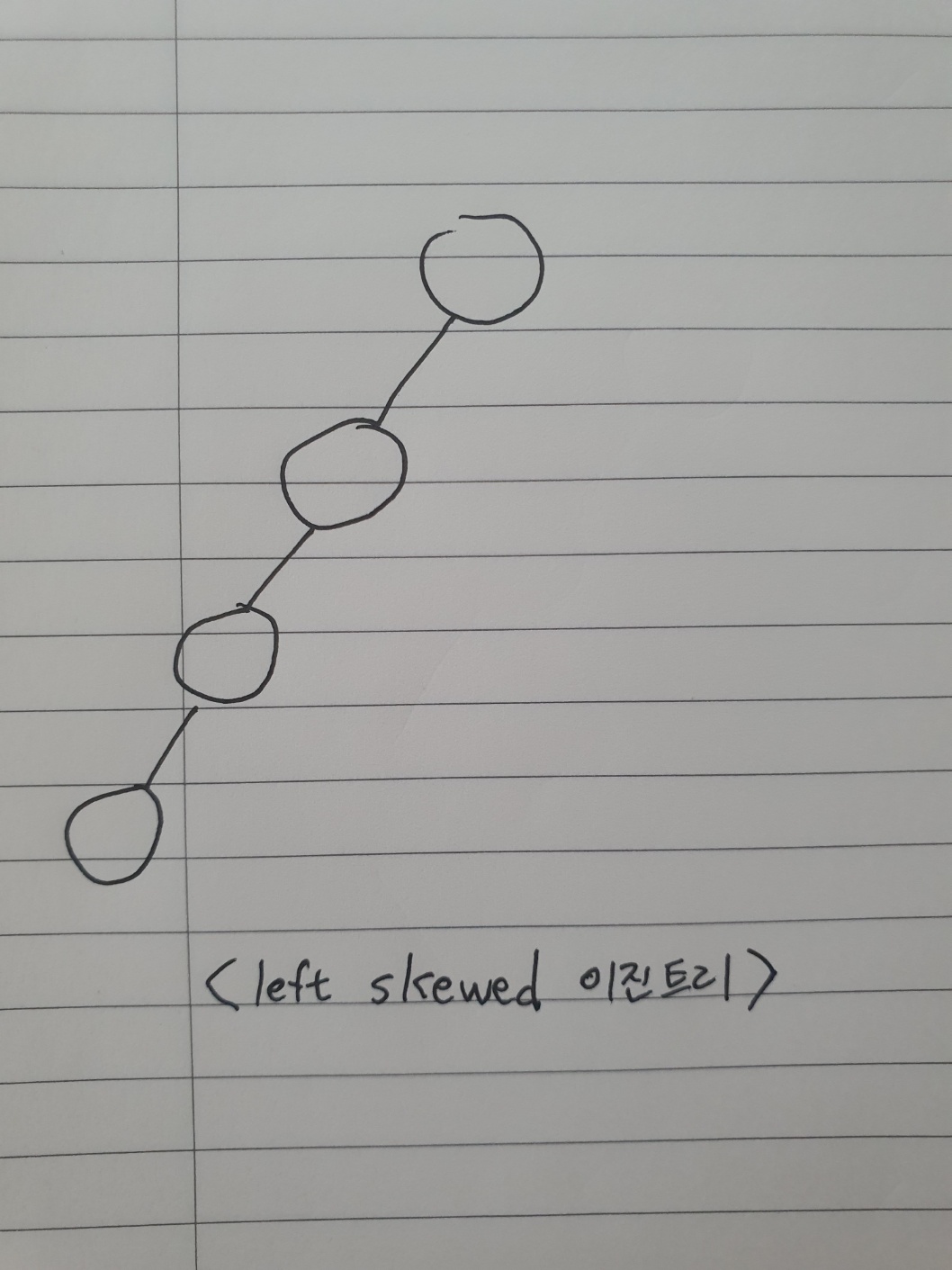
모든 부모 노드가 왼쪽 자녀노드만 가지면 left skewed binary tree

모든 부모 노드가 오른쪽 자녀노드만 가지면 right skewed binary tree라고 부른다.

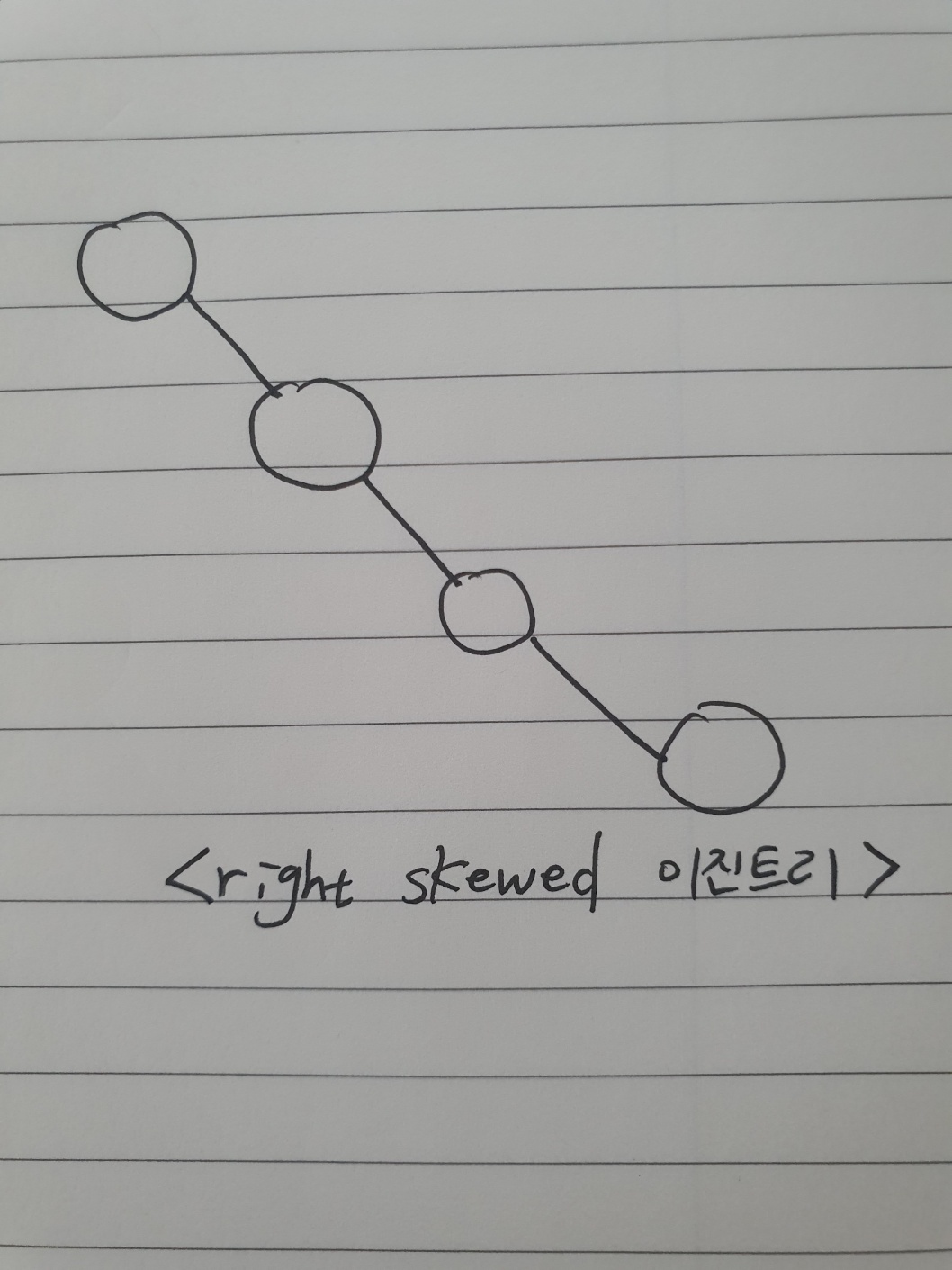
성능 면에서 선형인 연결 리스트 데이터 구조처럼 동작한다.

다음 시간에는 이진 탐색 트리에 대해 다루는 걸루~
바이바이~~

참고:
https://ko.wikipedia.org/wiki/%EC%9D%B4%EC%A7%84_%ED%8A%B8%EB%A6%AC#%EC%9D%B4%EC%A7%84_%ED%8A%B8%EB%A6%AC%EC%9D%98_%EC%86%8D%EC%84%B1
위키백과

https://www.youtube.com/watch?v=ohrwGtqeW-I&list=PLcXyemr8ZeoR82N8uZuG9xVrFIfdnLd72&index=7
쉬운 코드

면접을 위한 CS 전공지식 노트(주홍철 저)