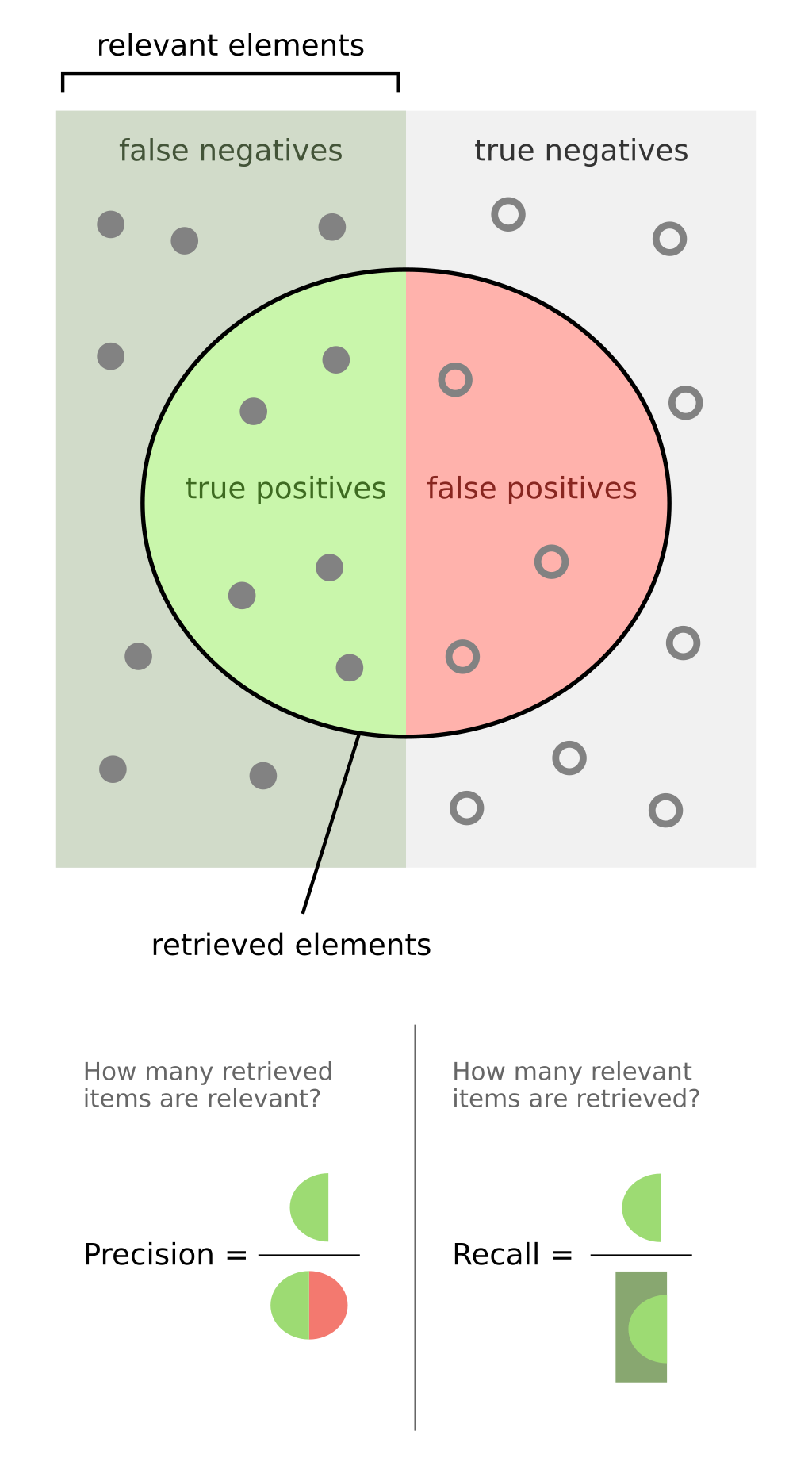
(자료: Wikipedia)

F-Score

• Precision (정밀도): 모델이 "맞다"라고 예측한 것 중에 실제로 맞은 비율
  (based on (realy) relevant things)

  $\text{Precision} = \frac{TP}{TP + FP}$

• Recall (재현율): 실제로 맞는 것 중에 모델이 맞다고 예측한 비율
  (over the retireved things from the test or experience)

  $\text{Recall} = \frac{TP}{TP + FN}$

여기서

• TP = True Positive (정답을 맞춘 경우)
• FP = False Positive (틀렸는데 맞다고 한 경우)
• FN = False Negative (맞는데 틀렸다고 한 경우)

F1-Score$

Balanced F-measure

F1 정의

• F1은 Precision과 Recall을 동일하게 중요하게 취급한다.
• F1은 Precision과 Recall의 조화평균 (harmonic mean)으로 정의한다:

• 산술평균(Arithmetic mean)은 단순 평균인데,
• 조화평균(Harmonic mean)은 두 값이 모두 크지 않으면 값이 작아 진다.
  즉, F1은 Precision과 Recall이 둘 다 높아야 높은 값을 가질 수 있고, 한쪽이라도 낮으면 크게 깎인다.

이를 TP, FP, FN으로 바꿔 쓰면:

$F_{\beta}\text{-Score}$

Generalized F-measure

• 하지만 경우에 따라 "재현율(Recall)이 더 중요"하거나 "정밀도(Precision)이 더 중요"할 수 있다.

  • 예: 질병 진단 → 놓치면 안 되니까 Recall ↑ 중요
  • 스팸 필터 → 잘못 차단하면 안 되니까 Precision ↑ 중요

• 이를 위해 β (베타) 파라미터를 사용한다.

$F_{\beta}\text{-Score}$

• β > 1 이면 Recall 쪽 가중치 ↑ (Recall을 더 중요시)
• β < 1 이면 Precision 쪽 가중치 ↑ (Precision을 더 중요시)
• β = 1 이면 F1이 됩니다.

• F1: Precision과 Recall을 균형 있게 평가.
• $F_{\beta}\text{-Score}$: Precision과 Recall 중 어느 쪽을 더 강조할지 $\beta$로 조절.

예시

간단 예시

• $\beta$ = 2 → Recall을 Precision보다 2배 중요하게 본다. 정밀도 가중
• $\beta$ = 0.5 → Precision을 Recall보다 2배 중요하게 본다. 재현율 가중

Precision이 더 높은 경우

가정:

• TP=80, FP=20, FN=40
• Precision $= \frac{80}{80+20} = 0.8000$
• Recall $= \frac{80}{80+40} = 0.6667$

계산

해석:

• Precision이 높은 상황이라 $F_{0.5}$가 가장 높고, Recall을 중시하는 $F_2$는 상대적으로 낮아짐.

Recall이 더 높은 경우

가정:

• TP=50, FP=50, FN=10
• Precision $= \frac{50}{50+50} = 0.5000$
• Recall $= \frac{50}{50+10} = 0.8333$

계산:

• F1 $\approx \mathbf{0.6250}$
• $F_{0.5}$ (정밀도 가중) $\approx \mathbf{0.5435}$
• $F_{2}$ (재현율 가중) $\approx \mathbf{0.7353}$

해석:

• Recall이 높은 상황이라 **$F_2$**가 가장 유리하게 나옴. 반대로 정밀도 쪽을 강조하는 $F_{0.5}$는 낮아짐.

핵심 포인트 요약

• F1: Precision과 Recall을 동일 가중으로 결합 → 둘 중 하나라도 낮으면 크게 깎임.
• $F_\beta$: $\beta>1$이면 Recall을, $\beta<1$이면 Precision을 더 중요하게 반영.

---

https://en.wikipedia.org/wiki/F-score