[확률/통계] AM<=GM<=HM 비교

같은 데이터라도 AM, GM, HM을 모두 계산할 수는 있지만,
항상 “같은 문제의 정답”이 되지는 않는다.
상황에 따라 적절한 평균이 달라진다.

계산 자체는 언제나 가능하다 (AM, GM, HM 다 나옴).
하지만 상황에 맞는 평균을 골라야 의미 있는 해석이 된다.

1. 이론적으로

• 수학적으로는 $[x_1, x_2, \dots, x_n]$ 같은 양수 집합이 있으면,
  언제든지 산술평균·기하평균·조화평균을 모두 계산할 수 있다.

• 실제로도 AM, GM, HM 값은 항상 존재하고, 관계식도 성립한다:

  $HM \leq GM \leq AM$

2. 하지만 "문제의 정답"은 다름

• 산술평균 (AM): “더해서 나누기” → 일반적인 값의 대표

  • 예: 시험 점수, 사람 키, 몸무게

• 기하평균 (GM): “곱셈/비율 구조” → 곱으로 누적되는 경우의 대표

  • 예: 성장률, 확률, 복리

• 조화평균 (HM): “역수/비율 구조” → 분모가 중요한 경우

  • 예: 평균 속도, 전기저항 병렬, F1-score

3. 예시 비교

네, 정확합니다 👍 제가 차근차근 정리해드릴게요.

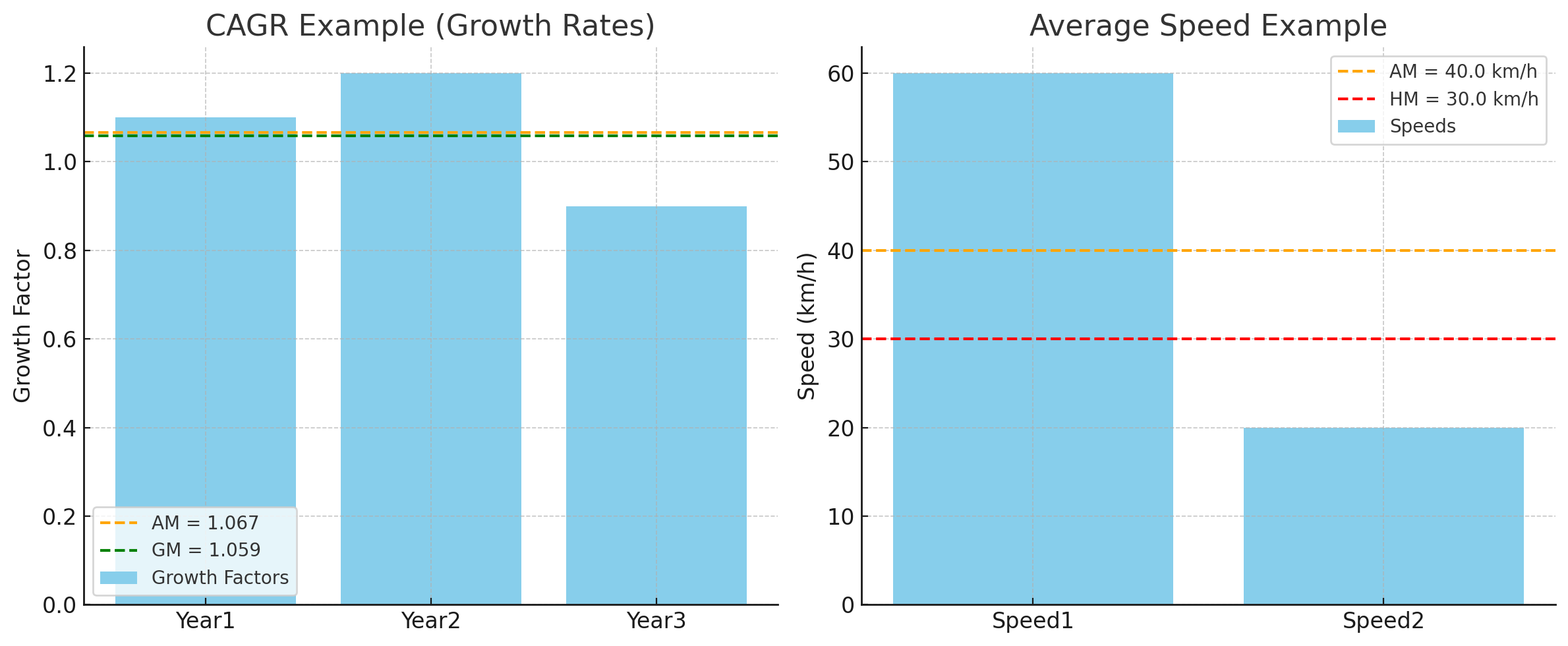
1. CAGR 예시

• 연도별 성장률:

  • 1년차: 1.10 (= +10%)
  • 2년차: 1.20 (= +20%)
  • 3년차: 0.90 (= -10%)

• 전체 누적 성장률:

  $1.10 \times 1.20 \times 0.90 = 1.188$

즉, 3년 동안 18.8% 성장한 셈이에요.

• 연평균 성장률(CAGR):

  $GM = (1.10 \cdot 1.20 \cdot 0.90)^{1/3} \approx 1.059$

  → 연평균 약 5.9% 성장
  

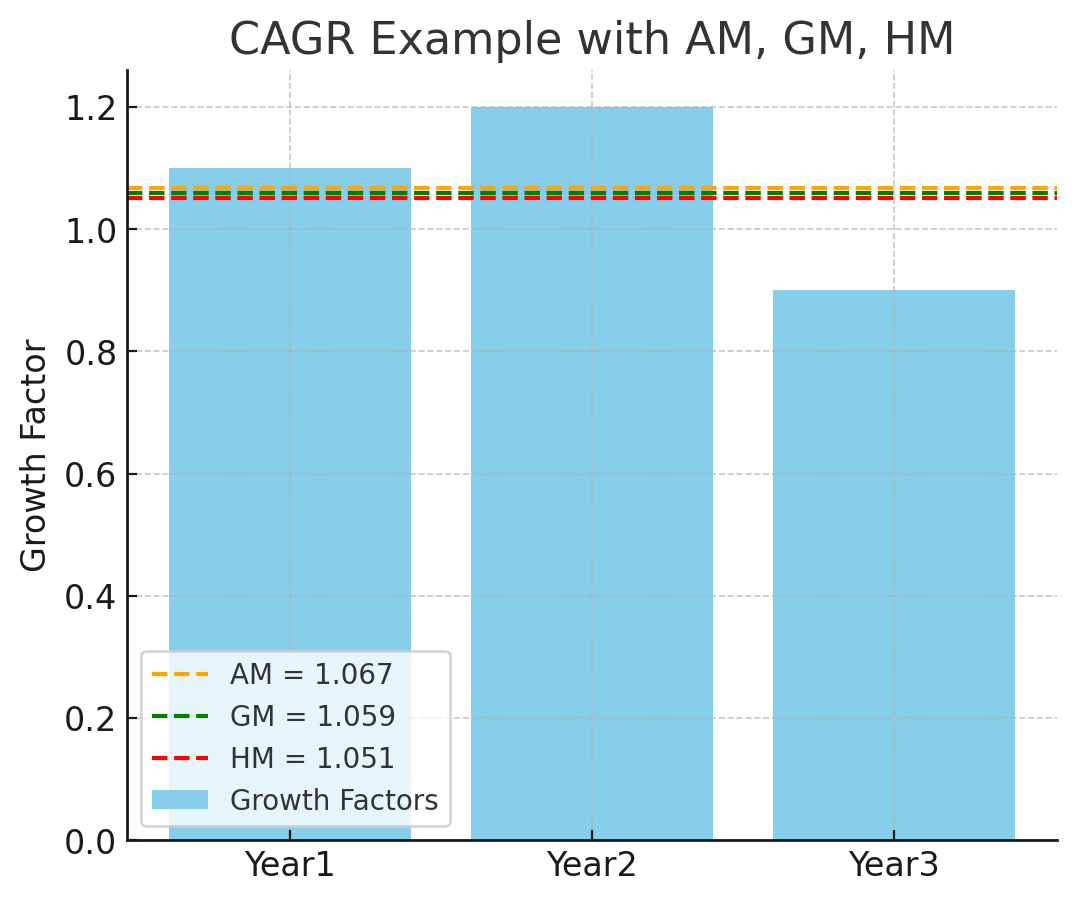
곱셈 구조라서 **기하평균(GM)**이 정답!

2. 단순 값 [2, 4, 6] 예시

• 산술평균 (AM)

  $(2+4+6)/3 = 4$

• 기하평균 (GM)

  $(2 \cdot 4 \cdot 6)^{1/3} = 48^{1/3} \approx 3.63$

• 조화평균 (HM)

  $3 / (1/2 + 1/4 + 1/6) = 3 / 0.9167 \approx 3.27$

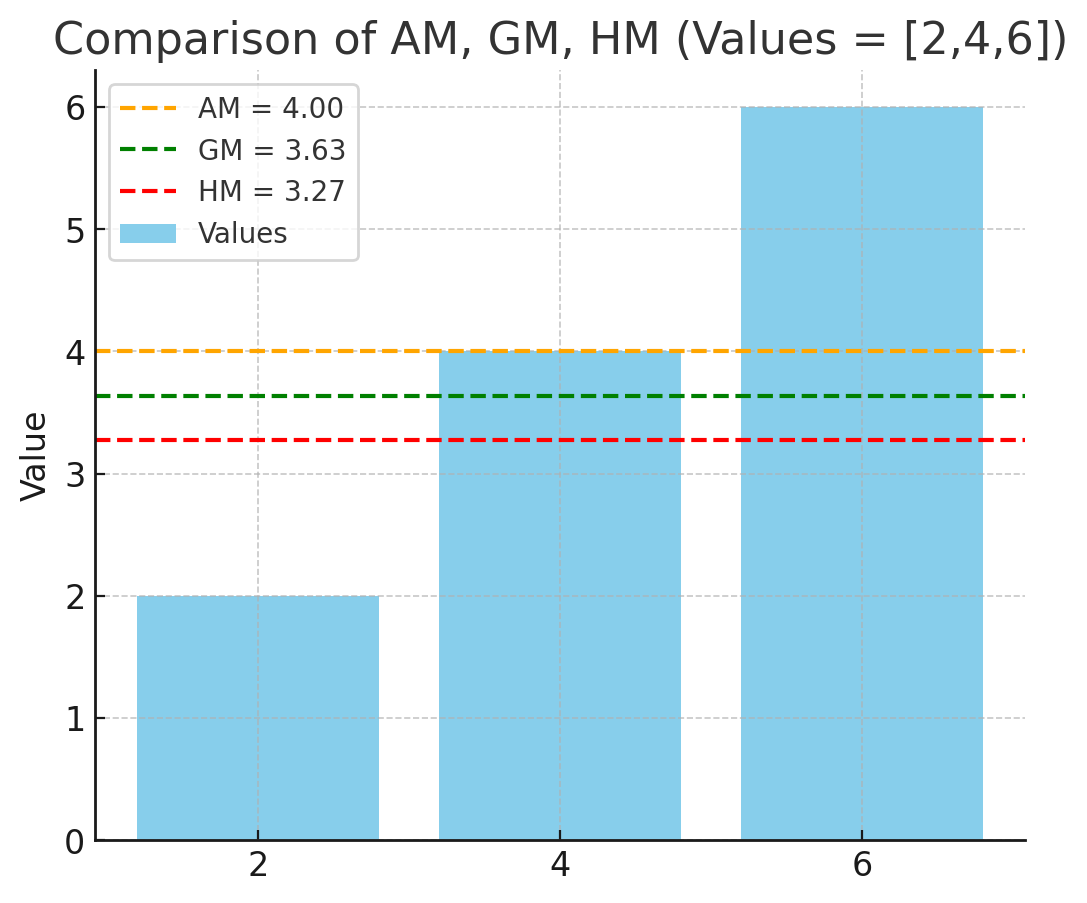
즉, 세 값은 다르지만, 같은 데이터에서 다 계산할 수 있다.
“시험 점수 평균” 같은 문제에서 HM을 쓰면 말이 안될 것이다. 😅