[Linear Algebra] Orthogonal to QR Factorization

Orthogonal and Orthonormal Sets

• Definition: A set of vectors $\begin{Bmatrix} \textbf{u}_1, \cdots, \textbf{u}_p \end{Bmatrix}$ in $\mathbb{R}^n$ is an orthogonal set
  if each pair of distinct vectors from the set is orthogonal
  That is, if $\textbf{u}_i \cdot \textbf{u}_j = 0$ whenever $i \neq j$
• Definition : A set of vectors $\begin{Bmatrix} \textbf{u}_1, \cdots, \textbf{u}_p \end{Bmatrix}$ in $\mathbb{R}^n$ is an orthonormal set
  if it is an orthogonal set of unit vectors
• Orthogonal or orthonormal set is also linearly independent, but not vice versa

Orthogonal Projection Perspective

• Consider the orthogonal projection $\textbf{b}$ onto $\textrm{Col} A$ as
  $\hat{\textbf{b}} = f(\textbf{b}) = A\hat{\textbf{x}} = A(A^T A)^{-1} A^T \textbf{b} = C \textbf{b}$
  where $C = A(A^T A)^{-1} A^T$
• We can see that the orthogonal projection is actually a linear transformation $f(\textbf{b}) = C\textbf{b}$
  where the standard matrix is defined as $C = A(A^T A)^{-1} A^T$
• If $A$ is orthonormal, $A^T A = \begin{bmatrix} \textbf{a}_1^T \\ \textbf{a}_2^T \\ \vdots \\ \textbf{a}_n^T \end{bmatrix} \begin{bmatrix} \textbf{a}_1 & \textbf{a}_2 & \cdots & \textbf{a}_n \\ \end{bmatrix} = I$
  Thus $\hat{\textbf{b}} = A\hat{\textbf{x}} = A(A^T A)^{-1} A^T \textbf{b} = A A^T \textbf{b} = C \textbf{b}$

Gram-Schmidt Orthogonalization

• Using Gram-Schmidt orthogonalization, we can make any basis to orthogonal or orthonormal basis

QR Factorization

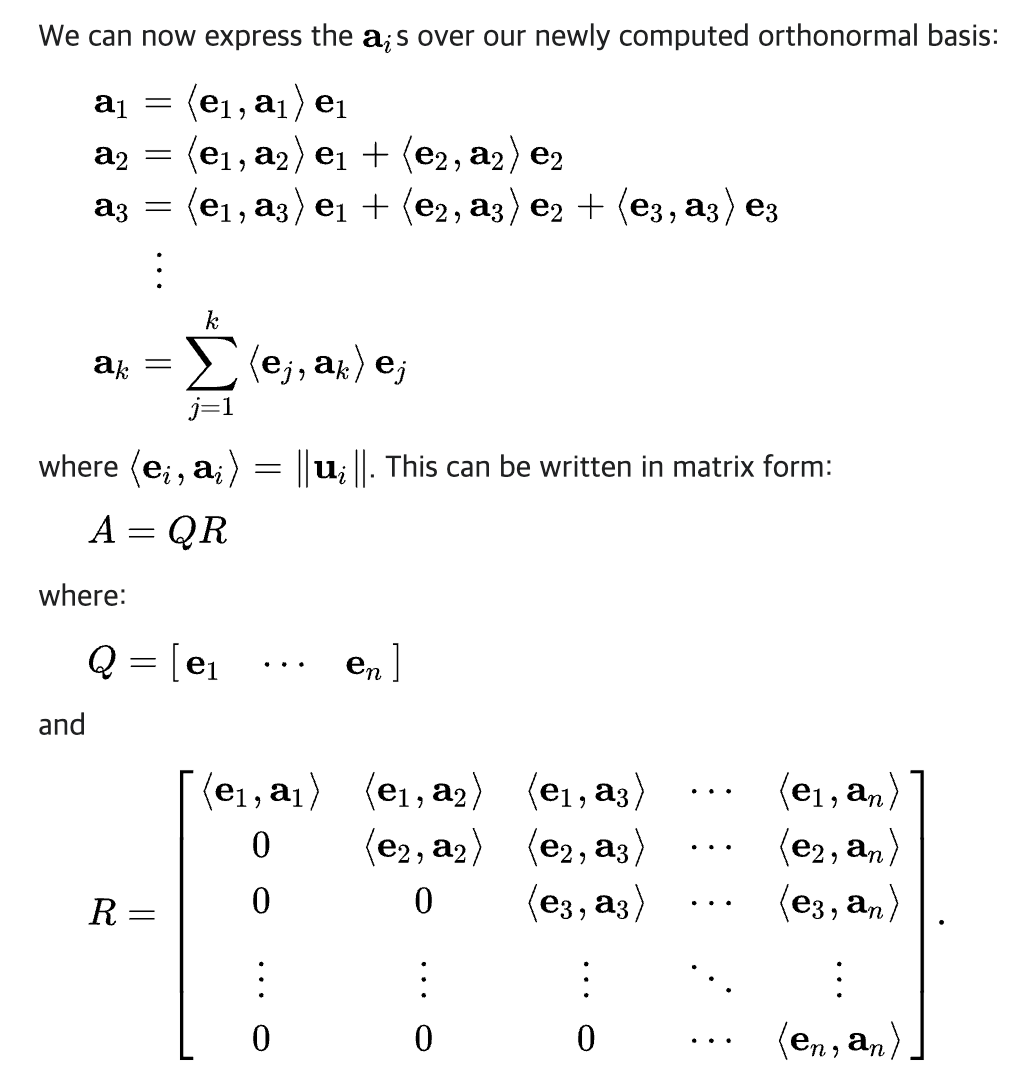
• If $A$ is an $m \times n$ matrix with linearly independent columns,
  then $A$ can be factored as $A = QR$
  where $Q$ is an $m \times n$ matrix whose columns form an orthonormal basis for $\textrm{Col} A$
  and $R$ is an $n \times n$ upper triangular invertible matrix with positive entries on its diagonal
• Using Gram–Schmidt orthogonalization, we can do QR factorization