실수

실수(1.123)는 정수부(1)와 소수부(.123)으로 표현할 수 있다.

2진수의 소수표현

사람의 표현 (10진법)

$2^3 = 1 \times 2 \times 2 \times 2 = 8$

$2^2 = 1 \times 2 \times 2 = 4$

$2^1 = 1 \times 2 = 2$

$2^0 = 1 \times (nothing) = 1$

$2^{-1} = 1 \div 2 = {1 \over 2} = 0.5$

$2^{-2} = 1 \div {2 \times 2} = {1 \over 4} = 0.25$

$2^{-3} = 1 \div {2 \times 2 \times 2} = {1 \over 8} = 0.125$

2의 0승이 1인 이유?

${2^1 \times 2^1} = {2^{(1+1)}} = 2^2 = 4$

${2^1 \times 2^0} = {2^{(1+0)}} = 2^1 = 2$

$2 \times x = 2$

$x = 1$

컴퓨터의 표현 (2진법)

10진법 -> 2진법

$8 = 1000$

$4 = 0100$

$2 = 0010$

$1 = 0001$

$0 = 0000$

$0.5 = 0.1000$

$0.25 = 0.0100$

$0.125 = 0.0010$

---

고정소수점(fixed point)

소수점이 고정되어있다.

아래와 같이 8비트의 공간이 있다고 하면,
$[00000000]$

이렇게나눈다
$[0/000/0000]$

첫번째 칸이 부호 칸으로 양수면 0, 음수면 1
두번째 칸이 정수부 Integer Parts
세번째 칸이 소수부 Fractional Parts

1.5를 표현하려면 $[0001.1000]$
1.75를 표현하려면 $[0001.1100]$
-2.25를 표현하려면 $[1010.0100]$

빠른 계산이 장점이나, 소수점이 고정이라 많은 숫자를 표현하지 못한다.

부동소수점(floating point)

부동이란?

부동은 움직이지 않는다(不動)는게 아니라 떠다닌다(浮動)라는 뜻이다.
소수점이 고정되어 있지 않고 좌우로 움직일 수 있다는 뜻이다.
그래서 변수 타입도 float라고 사용한다.

표현

가짜 예시

아래는 이해를 위해 필자가 가상으로 만든 8비트 부동소수점이다.

1.5라면
$[0001.1000] = [1.1000000] \times 2^0$

9.75라면
$[1001.1100] = [1.0011100] \times 2^3$

숫자가 0이 아니라면 무조건 맨 앞부분은 1이 된다.

실제

실제로는 보통 32비트(64비트는 double)로 표현하고 수식은 아래과 같다.

$\pm(가수부)\times2^{지수부}$

비트로 표현하면

$[0/0000'0000/0000'0000'0000'0000'0000'000]$

(보기 쉽게 하기 위해서 칸과 0의 4개씩 구분하였음.)

첫번째 칸(1비트)이 부호 칸으로 양수면 0, 음수면 1
두번째 칸(8비트)이 지수부
세번째 칸(23비트)이 가수부

지수부

지수부는 -127 ~ 128까지 지수를 표현 가능한데,
지수부에는 부호칸이 없으니 -127을 0으로 표현한다.
0 ~ 255 범위인 것이다.

예를 들어 $2^3$의 지수는 3이니 지수부에는 3 + 127인 130이 들어가면된다.

즉 이진법으로 $[1000'0010]$

가수부

가수부 맨 첫자리는 위에서 말했듯이 숫자가 0이 아니라면 무조건 맨 앞부분은 1이 된다.

그래서 아예 표현에서 빼버렸다.
(비트 하나라도 더 사용하기위해...ㅠㅠ)

9.75라면 $[1.0011100]$에서 맨앞자리 1을빼야하니
$[0011100...]$이 된다.

실수 표현

즉 9.75는

$[0/1000'0010/0011'1000'0000'0000'0000'000]$

아래에가서 확인해 볼 수 있다.
01000001000111000000000000000000

부동소수점 계산기
https://www.h-schmidt.net/FloatConverter/IEEE754.html

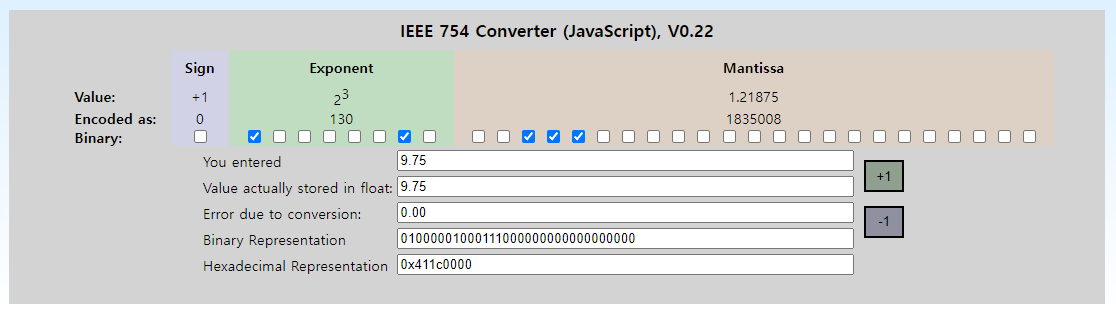
국산 부동소수점 계산기 (애드블록 해제해야 작동함)
https://t.hi098123.com/IEEE-754

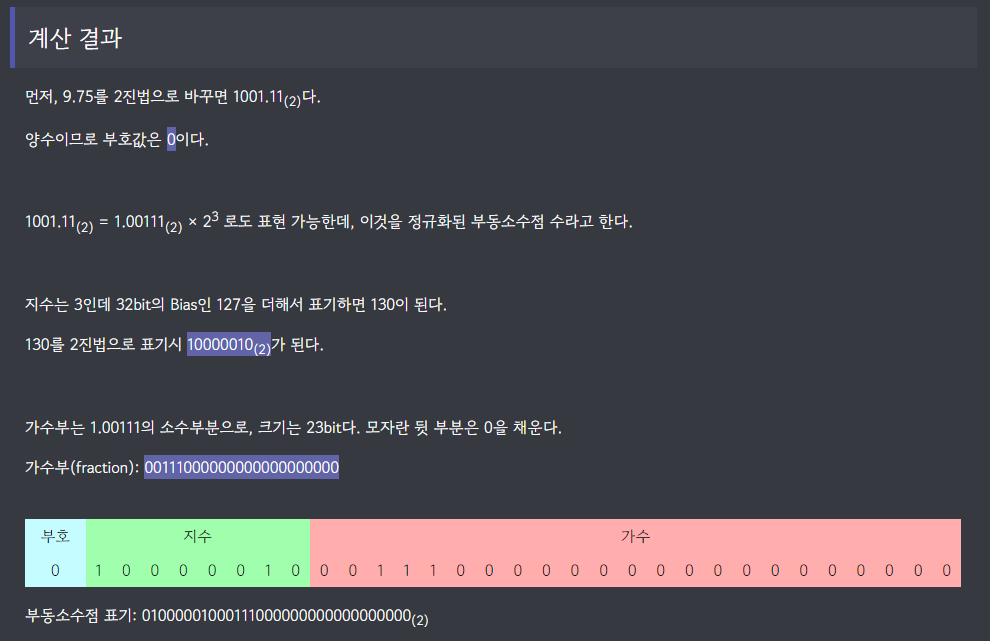
문제

고정소수점, 부동소수점 모두 프로그래밍 계산시

0.1 또는 1.2 등 대부분 실수는 나타낼 수 없고, 계산하면 오차값이 생긴다.

console.log(1.2)

// 1.2
// 그냥 실수를 주입했을 경우에는 toString으로 바로 변환하니 그대로 나온다.

console.log(0.1 + 1.1)

// 1.2000000000000002
// 계산을 하게되면 문제가 발생한다.

위의 부동소수점 계산기로 두드려봐도 마찬가지다.

2진수로 표현 가능한 0.5를 입력해보면

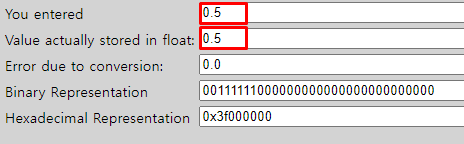
2진수로 표현 불가능한 1.1을 입력해보면

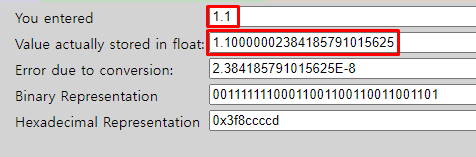
Value actually stored in float

즉 근사값으로 저장된다!

가수부에 저장가능한 비트까지만 저장이 되기 때문에 1.1과 가장 가까운 숫자가 저장될 뿐 정확한 수치가 아니다.

해결법

자바스크립트 해결법
https://velog.io/@jaybon/%EC%9E%90%EB%B0%94%EC%8A%A4%ED%81%AC%EB%A6%BD%ED%8A%B8-%EC%8B%A4%EC%88%98float-%EC%A0%95%ED%99%95%ED%9E%88-%EA%B3%84%EC%82%B0%ED%95%98%EA%B8%B0

참고자료

코딩 애플
https://www.youtube.com/watch?v=-GsrYvZoAdA

워라밸 프로그래머 되기
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=7rlaguswns7&logNo=221349728794