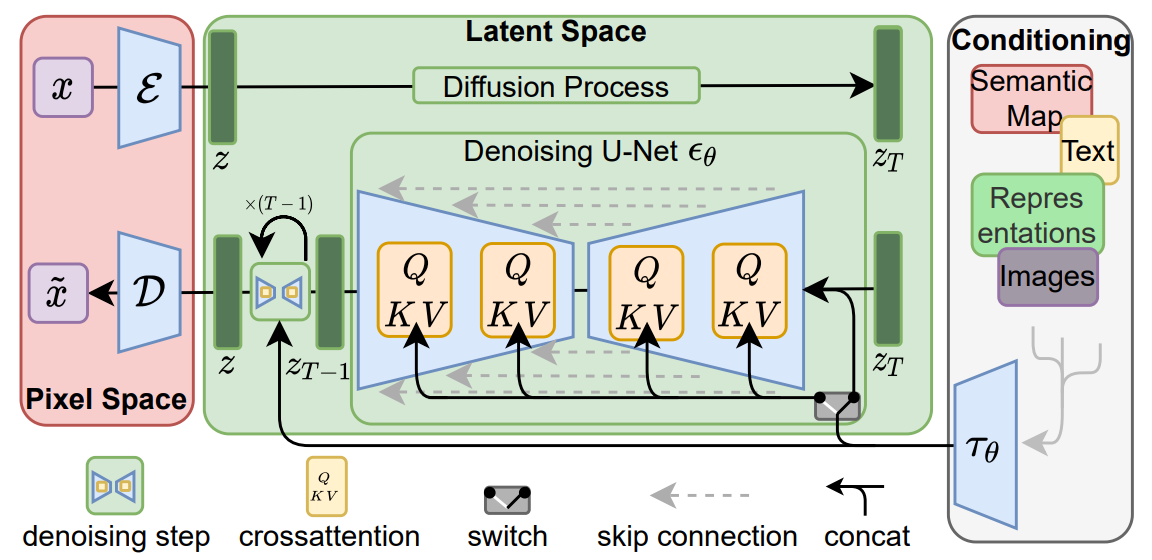
Conditioning MechanismsPermalink
다른 유형의 생성 모델과 마찬가지로 diffusion model은 원칙적으로 P ( z ∣ y ) P(z|y) P ( z ∣ y ) ϵ θ ( z t , t , y ) \epsilon_\theta (z_t, t, y) ϵ θ ( z t , t , y ) y y y
이미지 합성 측면에서 diffusion model의 생성 능력을 입력 이미지의 클래스 레이블이나 이미지를 흐릿하게 변형하는 것을 넘어선 다른 유형의 컨디셔닝과 결합하는 것이 이전 연구들과의 차이점 입니다.
다양한 입력 양식의 attention 기반 모델을 학습하는 데 효과적인 cross-attention 메커니즘으로 기본 UNet backbone을 보강하여 diffusion model을 보다 유연한 조건부 이미지 생성기로 만듭니다. 다양한 종류의 y y y y y y τ ϵ ( y ) ∈ R M × d r \tau _\epsilon (y) \in \mathbb R^{M \times d_r} τ ϵ ( y ) ∈ R M × d r τ ϵ \tau _\epsilon τ ϵ A t e e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d ) ⋅ V Ateention(Q, K, V) = softmax(\frac{QK^T}{\sqrt d})\cdot V A t e e n t i o n ( Q , K , V ) = s o f t m a x ( d Q K T ) ⋅ V Q = W Q ( i ) ⋅ ϕ ( z t ) , K = W K ( i ) ⋅ τ θ ( y ) , V = W V ( i ) ⋅ τ ϵ ( y ) Q = W^{(i)}_{Q} \cdot \phi (z_t), K = W^{(i)}_K \cdot \tau_\theta(y), V = W^{(i)}_V \cdot \tau_\epsilon(y) Q = W Q ( i ) ⋅ ϕ ( z t ) , K = W K ( i ) ⋅ τ θ ( y ) , V = W V ( i ) ⋅ τ ϵ ( y )
ϕ i ( z t ) ∈ R N × d ϵ i \phi_i(z_t) \in \mathbb R^{N \times d^{i}_\epsilon} ϕ i ( z t ) ∈ R N × d ϵ i ϵ θ \epsilon_\theta ϵ θ W V ( i ) ∈ R d × d ϵ , W Q ( i ) ∈ R d × d τ , W K ( i ) ∈ R d × d τ W^{(i)}_V \in \mathbb{R}^{d \times d_{\epsilon}}, W^{(i)}_Q \in \mathbb{R}^{d \times d_{\tau}}, W^{(i)}_K \in \mathbb{R}^{d \times d_{\tau}} W V ( i ) ∈ R d × d ϵ , W Q ( i ) ∈ R d × d τ , W K ( i ) ∈ R d × d τ
L L D M : = E ε ( x ) , y , ϵ ∼ N ( 0 , 1 ) , t [ ∥ ϵ − ϵ θ ( z t , t , τ θ ( y ) ) ∥ 2 2 ] L_{LDM} := \mathbb{E}_{\varepsilon_{(x)}, y, \epsilon \sim \mathcal{N}(0, 1), t}\left[\| \epsilon - \epsilon_\theta(z_t, t, \tau_\theta(y)) \|_2^2\right] L L D M : = E ε ( x ) , y , ϵ ∼ N ( 0 , 1 ) , t [ ∥ ϵ − ϵ θ ( z t , t , τ θ ( y ) ) ∥ 2 2 ]
τ θ 와 ϵ θ \tau_\theta 와 \epsilon_\theta τ θ 와 ϵ θ τ θ \tau_\theta τ θ
요약하자면, Cross-Attention 메커니즘은 다양한 입력 양식에 대해 강력한 조건부 이미지를 생성하도록 모델을 확장하며, 이를 통해 Diffusion 모델이 보다 유연하고 강력해집니다.
τ ϵ ( y ) ∈ R M × d r \tau_\epsilon (y) \in \mathbb R^{M \times d_r} τ ϵ ( y ) ∈ R M × d r
조건부 입력 y y y τ ϵ ( y ) \tau_\epsilon(y) τ ϵ ( y ) τ ϵ \tau_\epsilon τ ϵ
M M M d r d_r d r
Query, Key, Value 정의Q Q Q K K K V V V Q = W Q ( i ) ⋅ ϕ ( z t ) , K = W K ( i ) ⋅ τ θ ( y ) , V = W V ( i ) ⋅ τ ϵ ( y ) Q = W^{(i)}_{Q} \cdot \phi (z_t), K = W^{(i)}_K \cdot \tau_\theta(y), V = W^{(i)}_V \cdot \tau_\epsilon(y) Q = W Q ( i ) ⋅ ϕ ( z t ) , K = W K ( i ) ⋅ τ θ ( y ) , V = W V ( i ) ⋅ τ ϵ ( y )
ϕ ( z t ) \phi(z_t) ϕ ( z t ) τ ϵ ( y ) \tau_\epsilon(y) τ ϵ ( y ) y y y
UNet 중간 표현ϕ i ( z t ) ∈ R N × d ϵ i \phi_i(z_t) \in \mathbb R^{N \times d^{i}_\epsilon} ϕ i ( z t ) ∈ R N × d ϵ i
N N N d ϵ i d_\epsilon^i d ϵ i
Weight 정의W ( i ) V ∈ R d × d ϵ W^{(i)}V \in \mathbb{R}^{d \times d\epsilon} W ( i ) V ∈ R d × d ϵ W ( i ) Q ∈ R d × d τ W^{(i)}Q \in \mathbb{R}^{d \times d\tau} W ( i ) Q ∈ R d × d τ W ( i ) K ∈ R d × d τ W^{(i)}K \in \mathbb{R}^{d \times d\tau} W ( i ) K ∈ R d × d τ
d d d d ϵ d_\epsilon d ϵ τ ϵ ( y ) \tau_\epsilon(y) τ ϵ ( y ) d τ d_\tau d τ
L L D M : = E ε ( x ) , y , ϵ ∼ N ( 0 , 1 ) , t [ ∥ ϵ − ϵ θ ( z t , t , τ θ ( y ) ) ∥ 2 2 ] L_{LDM} := \mathbb{E}_{\varepsilon_{(x)}, y, \epsilon \sim \mathcal{N}(0, 1), t}\left[\| \epsilon - \epsilon_\theta(z_t, t, \tau_\theta(y)) \|_2^2\right] L L D M : = E ε ( x ) , y , ϵ ∼ N ( 0 , 1 ) , t [ ∥ ϵ − ϵ θ ( z t , t , τ θ ( y ) ) ∥ 2 2 ]
L L D M L_{LDM} L L D M E \mathbb{E} E x x x y y y ϵ ∼ N ( 0 , 1 ) \epsilon \sim \mathcal{N}(0, 1) ϵ ∼ N ( 0 , 1 ) t t t ϵ θ \epsilon_\theta ϵ θ τ θ ( y ) \tau_\theta(y) τ θ ( y ) y y y τ θ \tau_\theta τ θ ∣ ⋅ ∣ 2 2 | \cdot |_2^2 ∣ ⋅ ∣ 2 2
위의 학습내용은 저의 주관적인 내용이 포함되어 잘못 된 정보가 있을 수 있습니다. 참고용으로 읽어주시기 바랍니다.
Diffusers 학습 코드
Github