PCA(Principal Component Analysis)

• PCA는 주성분 분석이라고 하며 고차원의 데이터 집합을 낮은 차원의 데이터로 차원축소 하는 방법입니다.
• 데이터의 변수를 줄이는 것은 정확도를 좀 희생하는 것이지만 데이터를 쉽게 시각화 해보고 빠르게 분석할 수 있기 때문에 하는 과정 입니다.
• PCA의 아이디어는 가능한 많은 정보를 보존하면서 데이터 셋의 변수를 줄이는 것입니다.

표준화

• 표준화를 진행하는 이유는 초기 변수의 분산에 매우 민감하게 반응하기 때문입니다. 따라서 데이터를 비슷한 규모로 바꾸어주고 진행합니다.

$Z = \frac {value - mean}{standard deviation}$

표준화가 완료되면 모든 변수들이 동일한 척도를 가지게 됩니다.

공분산 행렬 계산

• 공분산 행렬을 계산하는 것은 변수사이에 어떤 관계가 있는지를 확인하는 것이 목적이고 때때로 변수가 중복된 정보를 가져 높은 상관관계를 가지기 때문에 이를 식별하기 위해 구하는 것입니다.
• 공분산 행렬은 PxP로 대칭행렬이어야 합니다.
• 다음은 3차원 데이터의 공분산 행렬의 예시로 3X3입니다.

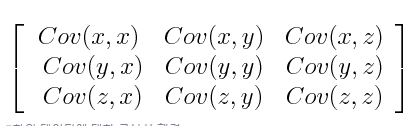
• 이때 중요한 것은 공분산의 부호인데 다음과 같은 의미를 가집니다.
  • 양수 : 두 변수가 함께 증가하거나 감소 (상관있음)
  • 음수 : 하나는 증가하고 다른 하나는 감소 (역상관)

공분산 행렬의 주성분 식별

특징 벡터

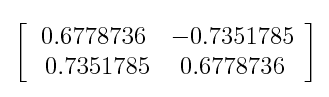
• 위와 같이 공분산 행렬이 있다면 다음과 같이 고유 벡터와 고유값을 알 수 있습니다. (구하는 방법은 너무 수학적인 내용이라 선형대수학에 eigenvalue를 검색해보시면 쉽게 구하는 방법을 아실 수 있을겁니다.)

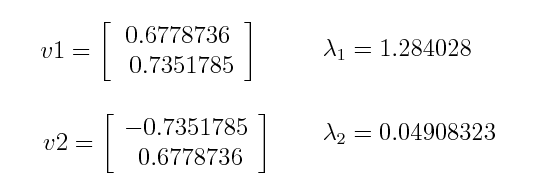
데이터 재구성

• 고유 벡터로 구성된 특징 벡터를 사용하여 원래 축의 데이터 방향을 주성분 분석으로 바꾸게 됩니다. 그 과정은 다음의 식처럼 특징 벡터의 전치에 원본 데이터셋의 전치를 곱하여 구합니다.

$Final DataSet = FeatureVector^T * StandardizedOriginalDataSet^T$

평균 센터링

다음으로 평균을 중심으로(0,0) 보내기 위해 평균값을 구해서 빼는 작업을 해주면

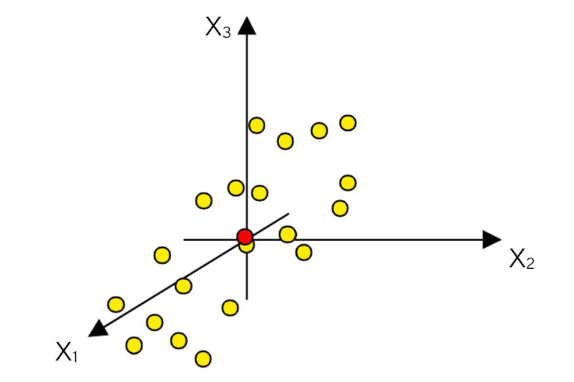
원점을 중심으로 데이터의 분포를 확인할 수 있습니다.

---

참고

• iris데이터 시각화
• Sartorius(개념 참고)
• builtin(개념 참고)

혹시 수학적으로 디테일한 부분이다보니 수학적으로 더 알고 싶은 분들은 해당 논문을 한번 읽어보시면 더 도움이 될것 같습니다.

• A Tutorial on Principal Component Analysis(논문)