1. Why ranked retrieval
(Boolean search : 정보 검색 시 AND, OR, NOT과 같은 연산자를 사용하여 검색하는 방식이다.)
- 단어를 통해 검색할 때 Boolean을 이용해서 검색한다면 해당 문서나 글에 단어가 존재하는지 여부만 알려주고 몇 번 나왔는지 순서는 어떠한지 등 상세한 정보들을 알 수 없다.
- 이는 법과 같이 해당 단어가 존재하는 모든 파일을 확인해야 하는 작업에서는 선호하지만 대부분의 유저의 경우 선호하는 방식이 아니다.
- 검색 하기 위한 query를 작성하는 스킬에 따라 정보의 양이 너무 많거나 적어짐
- 간단한 아이디어
- 처음에는 score를 0과 1사이로 두고 연관이 클 수록 1 적을수록 0
- 찾은 단어가 더 많이 나온 문서나 파일의 score가 더 높다.
1.1 Jaccard coefficient
- 일반적으로 사용되는 두 집합의 중첩 측도로 사용됩니다.
(A≠0 or B ≠ 0)
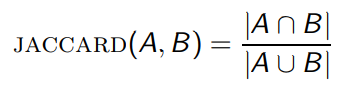
-
다음과 같이 계산이 가능하며
-
JACCARD(A,A) = 1
-
JACCARD(A,B) = 0 if A∩B = 0
-
두 집합의 크기는 동일할 필요는 없으며 값은 항상 0과 1사이입니다.
-
ex)
- Query: “ides of March”
- Document : “Caesar died in March”
- A∪B = (”ides”, “of”, “March”, “Caesar”, “died”, “in”) = 6, A∩B = (”March”) = 1
- JACCARD(q,d) = 1/6
-
문제점
- 여전히 문서에서 등장 횟수는 체크할 수 없음
- 잘 나오지 않는 단어의 정보를 고려하지 못함
2. Term freauency
- 기존에 존재여부만 확인한 matrix {0,1} boolean
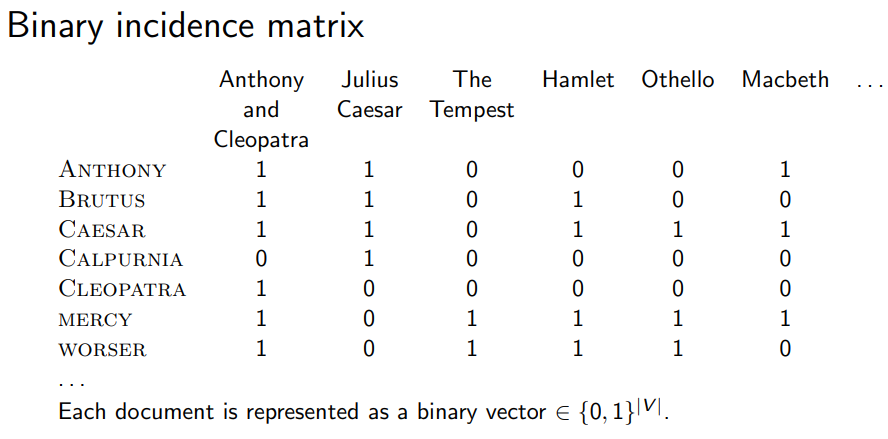
- 각 Document에 단어가 얼마나 나오는지 확인하는 matrix {0,1}→N
2.1 Bag of Words(BOW) model
- 순서를 고려하지 않고 단어만 추출하는 모델
- 가방에서 단어를 꺼내는 것과 같은 모델 일단 순서나 위치 정보는 무시
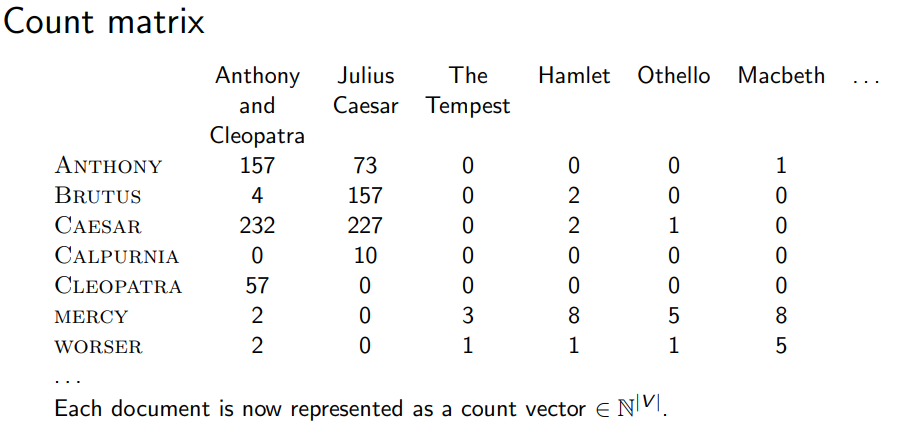
2.2 Term frequency (TF)
- 한 문서에서 단어(Term)가 몇 번 나왔는지를 계산 (클 수 록 중요도가 높은 단어)
- ex) 한 문서에 “Term” 이라는 단어가 1번 등장하면 tf = 1 , 10번 등장하면 tf = 10
- tf가 위 예제처럼 10배 차이가 난다면 해당 문서가 해당 단어에 10배 더 관련 있는지는 의문이다.
Law frequency → Log frequency
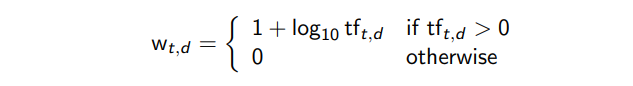
- 기존 tf의 값을 Log Scale로 변환해준다.
3. TF-IDF Weighting
단어의 tf만으로 중요도를 계산하기에는 무리가 있다.
- is, a등과 같이 불용어가 있기 때문
3.1 Document frequency (DF)
-
단어 “A”가 전체 문서 중 몇개의 문서에 존재 하는지를 계산
-
이때 df는 중요한 정보를 가진 단어일 수 록 전체 문서 중 일부 문서에서만 존재할 것이다.
-
ex)
- 전체 문서의 수 100
- “나” 라는 단어는 100개의 문서에서 존재 “알츠하이머”라는 단어는 1개의 문서에서 존재
- 그렇다면 df가 1인 “알츠하이머”가 정보력이 큰 Rare Term이다.
-
따라서 df는 작을 수 록 단어의 중요도가 높다.
-
IDF weight
- df의 경우 작을 수 록 정보력이 크기 때문에 inverse를 취해서 사용
- tf와 마찬가지로 Log Scale로 변환
3.2 TF-IDF Weighting
- 하나의 Term에 대한 중요도를 TF와 IDF 두 가지를 곱하여 계산한다.
- tf의 경우 문서마다 값이 달라지기 때문에 tf-idf의 값은 문서마다 다르다.
4. The Vector Space Model
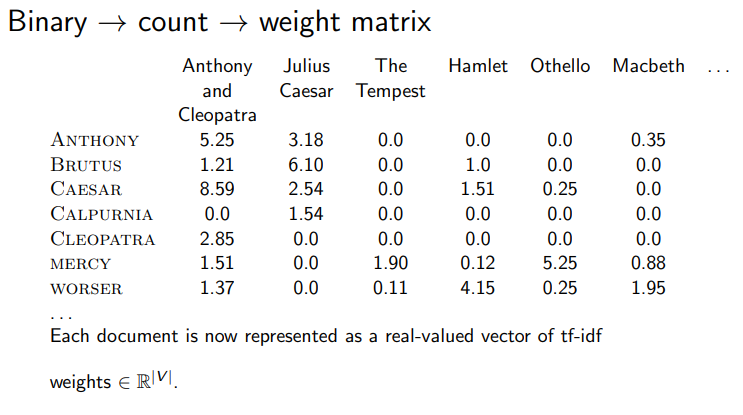
Log Scale을 진행하며 Matrix는 실수 공간으로 변환 된다.
- Term이 많아 질 수 록 차원의 수 도 증가한다.
- Query를 하나의 짧은 문서로 본다면 문서들 간의 유사도를 구할 수 있는 방법이 있을까?
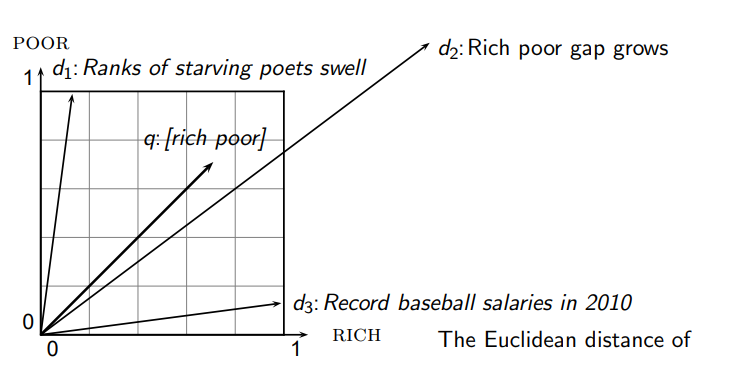
- 다음과 같이 문서화의 벡터화를 진행했을 때 단순히 거리를 이용하여 계산하면 안된다.
- 따라서 거리 대신 각도를 사용
4.1 Cosine Similarty
다음과 같이 계산할 수 있다.
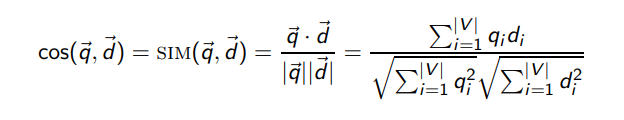
- 벡터의 길이는 normalized를 진행해서 사용 (단위벡터로 만들어준다.)
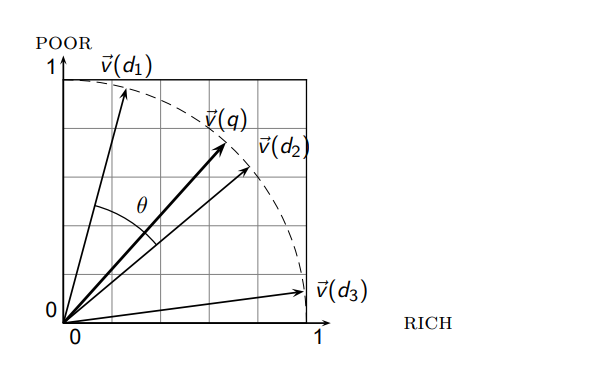
- EX)
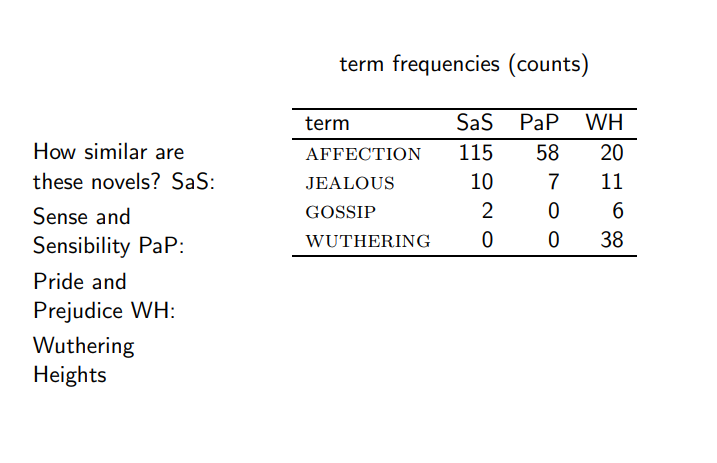
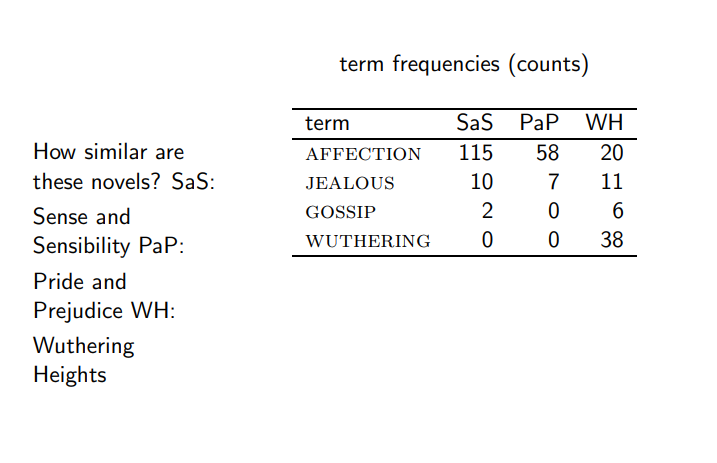
- 다음과 같이 각 term이 문서에서 등장한 수를 센 Count Matrix가 있다면
-
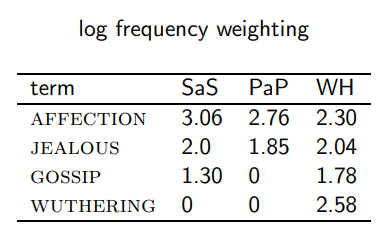
각각을 1 + log(p) 로 변환
-
각 문서 벡터의 normalization을 진행해줍니다.
-
|SaS| = √(3.06^2 + 2.0^2 + 1.30^2)롤 SaS의 각 값을 나눠줌 다른 문서도 동일
-
SaS와 PaP두 문서의 Cosine Similarty를 구하는 것은
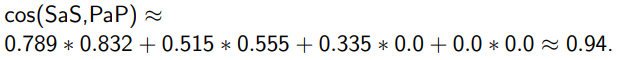
참고자료
참고
