오늘부터는 데이터를 다루는 법을 배워 보려고 합니다. 그중 기초통계를 가설을 세워 확인 하는 방법을 배워보겠습니다.

---

가설

가설을 세우는 이유는 연구한 값이 맞는지 통계적으로 검증 할 때 사용합니다.
가설 검증 3단계로 진행됩니다.
1. 귀무가설과 대립가설을 수립합니다.
2. 검정을 위한 표본추출 또는 확률실험을 설계합니다.
3. 의사결정의 기준을 정합니다.

귀무가설(Null Hypothesis)

귀무가설이란 기존에 알려진 사실으로 "새로울 것이 없다" 라고 가설을 세우는 것입니다.
부정적, 소극적, 보수적, 전통적인 가설이며, 제발 틀리길 바라는 가설입니다.

대립가설(Alternative Hypothesis)

대립가설이란 귀무가설과 상반된 입장을 가진 가설으로써, "새로울 것이 있다" 라고 가설을 세우는 것입니다.
긍정적, 적극적, 진취적, 미래지향적인 가설이며, 맞기를 바라는 가설입니다.

예시

각 100명의 A와 B집단의 성적은 B 집단이 같거나 높다. 라고 가설을 세웠을 때
귀무 가설 : B집단이 같거나 높다.
대립 가설 : A집단이 높다.
여기서 중요한건 P-Value인데 쉽게 생각하면 B집단과 A집단의 점수 차이가 5점 이상 있어야 검증 된다는 것입니다. 확률상 0.05(5%)미만의 값은 우연히 일어날 확률이 적다고 판단하고 가설을 기각하게 됩니다.

---

통계

중위수와 평균

input

import numpy as np
data=np.array([4,5,1,2,7,2,6,9,3])
v_mean = np.mean(data)
v_median = np.median(data)
print(v_mean)#평균
print(v_median) #중위수

output

4.333333333333333
4.0

---

분산과 표준편차

input

import numpy as np

points=np.array([20,80,90,95,87,89,95,99,97,100,60,70,77,88,89,89,90])
v_var = np.var(points) # 분산
v_std = np.std(points) # 표준편차
v_aver = np.max(points)-np.min(points) # 평균
print(v_var)
print(v_std)
print(v_aver)

output

352.1799307958477
18.766457598487992
80

---

사분위수

input

import numpy as np
points=np.array([20,80,90,95,87,89,95,99,97,100,60,70,77,88,89,89,90])
for val in [20,80,100]:
    d=np.percentile(points,val)
    print(str(val)+'%',d)
a,b,c=np.percentile(points, [25,50,75])
print("-" * 10)
print("사분위수")
print(a) #1사분위수
print(b) #2사분위수
print(c) #3사분위수

output

20% 77.6
80% 95.0

100% 100.0

사분위수
80.0
89.0
95.0

---

카이제곱 검정

input

from scipy import stats 
data1=[4,6,17,16,8,9]
data2=[10,10,10,10,10,10]
chis=stats.chisquare(data1,data2) #카이제곱 검정
chis

output

Power_divergenceResult(statistic=14.200000000000001, pvalue=0.014387678176921308)

카이제곱을 통해 가설 검증을 합니다.
카이제곱 검정이란
1. Goodness of fit test(적합도 검정) : 관찰 된 비율 값이 기대값과 같은지 검정
2. Test of homogeneity(동질성 검정) : 두 집단의 분포가 동일한지 검정
3. Test for independence(독립성점정)

• 기대빈도는 두 변수가 서로 상관 없고 독립적이라고 기대하는 것을 의미하며, 관찰 빈도와의 차이를 통해 기대 빈도의 진위여부를 밝힘
• 귀무가설 : 두 변수는 연관성이 없음(독립)
• 대립가설 : 두 변수는 연관성이 있음(독립x)

---

data를 활용하여 검정

데이터 파일 제 깃허브에 데이터 파일을 넣어 놨습니다. 직접 만드셔서 검정하셔도 되고 제 것으로 하셔도 됩니다.
input

import pandas as pd 
survey=pd.read_csv('d:/data/smoke/result.csv')
data=pd.crosstab(survey.Smoke, survey.Exer) # 집계함수
print(data)
result=stats.chi2_contingency(observed=data) # 카이제곱검정
print(result[0]) #검정통계량
print(result[1]) #pvalue 점근유의확률

output
Exer Freq Some
Smoke
Heavy 7 3
Never 87 84
Occas 12 4
Regul 9 7
4.574966550693501
0.20570012488442274

pandas 모듈을 통해 csv 파일을 불러 오고 crosstab함수를 통해 csv안의 변수를 활용하여 데이터를 검정할 수 있습니다. 가설은 Smoke(흡연)와 Exer(운동)의 연관성이 있는지 없는지 확인 해보았습니다.
p-value 값이 0.2 즉 0.05를 초과하므로 데이터가 유의하지 않고 둘의 연관성이 있음을 확일 할 수 있습니다.

---

단일표본 T - 검정

input

import numpy as np 
#np.random.seed(1) # 랜덤시드 고정
#normal(평균,표준편차) 
heights=[180+np.random.normal(0,5) for a in range(20)]
print(heights)
#단일표본 t검정
result=stats.ttest_1samp(heights, 175)
result

output

176.22801029501673, 186.26434077616645, 182.56464910209004, 178.50953582448642, 182.44259073268748, 179.62214143489473, 185.65814693725713, 187.599084082111, 190.9278770326658, 173.0175183225593


TtestResult(statistic=4.172940001921022, pvalue=0.0024011145533970094, df=9)

키를 표현하기 위해 180이내의 값을 랜덤 시드로 정하고 T 검정을 통해 가설 확인합니다.
175을 평균으로 잡았을때 p-value가 0.05미만이므로 귀무 가설이 채택되어 175는 평균이 아니게 됩니다.

T - 검정이란
가설 검정을 사용하여 하나 또는 두 모집단의 평균을 평가하는 도구입니다.

---

독립표본 T - 검정

input

#독립표본 t검정: 2개의 서로 다른 그룹의 차이를 검정하는 기법 
#귀무가설 : 두 그룹 학생들의 평균키는 같다.
#대립가설 : 두 그룹 학생들의 평균키는 같지 않다.
np.random.seed(0)
group1=[170+np.random.normal(0,5) for a in range(20)]
group2=[175+np.random.normal(0,10) for a in range(20)]
result1=stats.ttest_ind(group1, group2)
print(result1)

output

Ttest_indResult(statistic=-0.9366113029939336, pvalue=0.3548732604726367)

0.05이상이므로 대립가설을 기가하고 귀무가설이 채택되어 평균키는 같다라는 의미로 나오게 됩니다.

---

대응표본 T - 검정

input

#대응표본 t검정
#귀무 가설: 복용 전후의 체중 차이가 없다.
#대립 가설: 복용 전후의 체중 차이가 있다.
np.random.seed(1)
before=[60+np.random.normal(0,5) for _ in range(20)]
after=[w * np.random.normal(0.99, 0.02) for w in before]
result=stats.ttest_rel(before, after) 
print(result)

output

TtestResult(statistic=2.9154993563693186, pvalue=0.008871163766572827, df=19)

P - Value가 0.05미만이므로 유의미하다고 받아 들여 체중에 차이가 난다고 할 수 있습니다.

---

분산분석

input

#일원배치 분산분석(anova 분석) - 3개 이상의 그룹
#귀무가설 : 4개의 교육훈련 기법간의 차이가 없다.
#대립가설 : 4개의 교육훈련 기법간의 차이가 있다.
import matplotlib.pyplot as plt 
a=[66,74,82,75,73,97,87,78]
b=[72,51,59,62,74,64,78,63]
c=[61,60,57,60,81,55,70,71]
d=[63,61,76,84,58,65,69,80]
plot_data=[a,b,c,d]
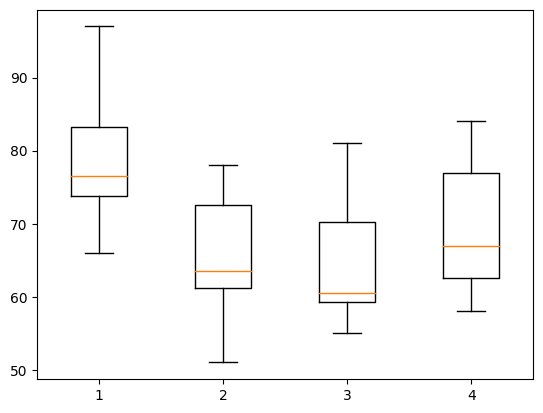
plt.boxplot(plot_data)
plt.show()
#박스플롯, 상자수염그림
stats.f_oneway(a,b,c,d) # 분석

output

F_onewayResult(statistic=4.2210931159803815, pvalue=0.013933707427484204)

그림으로 분석결과를 출력할 수 있습니다.눈으로도 확인 가능하지만 분산분석을 통해 확인해보면 p-value가 0.05미만 이기 때문에 교육기관에 차이가 있음을 알 수 있습니다.

---

데이터 사용한 분산 분석

데이터 파일 제 깃허브에 데이터 파일을 넣어 놨습니다. 직접 만드셔서 검정하셔도 되고 제 것으로 하셔도 됩니다.
input

#귀무가설: 세가지 비료의 수확량은 차이가 없다.
#대립가설: 세가지 비료의 수확량은 차이가 있다.
data=pd.read_csv('d:/data/fertilizer/fertilizers.csv')
result=stats.f_oneway(data['A'],data['B'],data['C'])
result

output
F_onewayResult(statistic=3.7551268418654105, pvalue=0.04762461989261837)

0.05미만 이기에 대립가설을 채택하여 세가지 비료는 차이가 있다고 볼 수 있습니다.

---

오늘은 기초통계와 가설검정에 대해 공부 해보았는데 저도 아직 헷갈리는 부분도 있기 때문에 틀린 부분이 있다면 고치도록 하겠습니다. 어려운 내용이기에 많이 헤매게 되는데, 저희는 항상 대립가설쪽이라고 생각하시면 편한거 같습니다.플러스로 p-value가 낮아야 좋다. 두가지를 생각하시면 편하게 이해가 가능하다고 생각합니다. 그럼 오늘도 고생하셨습니다.

😁 power through to the end 😁