Python P-Value

Jayce_97·2023년 5월 23일

Python 데이터

목록 보기

2/4

오늘은 통계에서 자주 사용되는 P-Value라는 것에 대해 배워보겠습니다.

P-Value

귀무가설 유의성 검정에서 사용되는데, 귀무가설이 맞다고 가정할 때, 관찰된 결과가 일어날 확률입니다. 즉, 해당 데이터의 값이 유의한지 아닌지를 알려주는데 사용됩니다.
내 주장과 일반적으로 반대되는 가설인 귀무가설을 참이라고 가정했을 때, 내가 관측한 데이터의 통계랑이 귀무가설을 지지할 확률을 P-value라고 정의할 수 있습니다.
그림으로 이해하자면
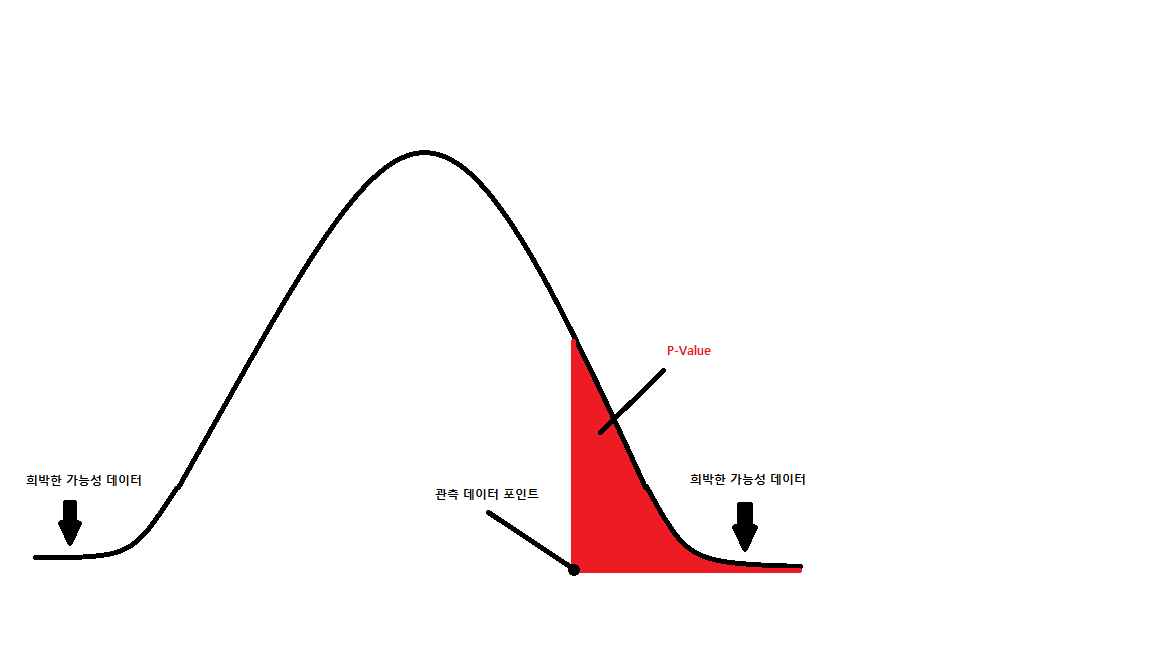
P-Value

다음과 같이 이해 할 수 있습니다.

P-value 값 측정해보기

input

from math import sqrt 
from numpy import mean 
from scipy.stats import sem, t 

def independent_ttest(data1, data2):
    mean1, mean2=mean(data1), mean(data2)
    #표준오차(표본평균의 표준편차) 계산
    se1, se2=sem(data1), sem(data2) 
    sed=sqrt(se1**2 + se2**2) 
    #t통계량
    t_stat=(mean1-mean2)/sed 
    #자유도(샘플수-1)
    df=len(data1)+len(data2)-2 
    #pvalue 계산, cdf 누적분포함수
    p=(1.0-t.cdf(abs(t_stat),df))*2.0
    return t_stat, p
X=[3.52, 2.58, 3.31, 4.07, 4.62, 3.98, 4.29, 4.83, 3.71, 4.6, 3.9, 3.2]
y=[2.48,2.27,2.47,2.77,2.98,3.05,3.18,3.46,3.03,3.25,2.67,2.53]
alpha=0.05 #95% 신뢰수준
t_stat,p=independent_ttest(X,y)
print('t=',t_stat)
print('p=',p)
if p >alpha: # pvalue가 0.05보다 크면
    print('귀무가설 채택, 대립가설 기각')
else:
    print('귀무가설 기각, 대립가설 채택')

output

t= 4.753794322942115
p= 9.578922820874247e-05
귀무가설 기각, 대립가설 채택

9.578922820874247e-05에서 e-05란 10^-5를 뜻합니다. 즉 0.00009578922820874247로 P-Value의 값이 0.05보다 작기 때문에 귀무가설을 기각하고 대립가설이 채택되게 됩니다.

확률분포

input

#확률분포: 어떤 사건에 어느 정도의 확률이 할당되었는지를 묘사한 것
#누적분포함수(cumulative distribution function))
#  모든 사건에 대해 구간을 정의하기가 어려우므로 시작점을 마이너스무한대로 설정하고 
#  마이너스무한대 ~ -1, 마이너스무한대 ~ 0, 마이너스무한대 ~ 1 식으로 구간을 정의하는 방법
import matplotlib.pyplot as plt 
import numpy as np 
import scipy as sp 

xx = np.linspace(-8, 8, 100)
#print(xx)
#정규분포 생성, loc 분포의 기대값, scale 분포의 표준편차
rv = sp.stats.norm(loc=1, scale=2)
#누적분포함수
cdf = rv.cdf(xx)
#확률밀도함수(누적분포함수를 미분한 함수)
pdf = rv.pdf(xx)

print(xx[:5])
print(cdf[:5])
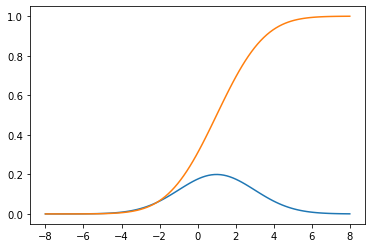
plt.plot(xx, pdf)
plt.plot(xx, cdf)
plt.show()