상관계수 (R : Correlation Coefficient)
→ 두 변량 X,Y 사이의 상관관계의 정도를 나타내는 수치, -1,과 1사이의 값을 가지면 절대값이 1에 가까울 수록 두 변량 사이의 상관관계의 정도가 높음
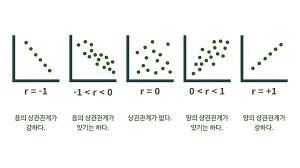
- 상관도 : 두 변량 사이의 관계를 대략적으로 파악할 수 있는 그래프를 상관도라고 한다.
- 단순상관계수 : 상관도 모양이 대체로 직선인 경우에는 단순상관계수를 사용하며 상관도 모양이 곡선인 경우에는 상관비를 사용한다.
- 상관분석 : 상관계수를 이용하여 변수와 변수 사이의 직선 관계를 분석하는 것을 상관분석이라고 한다.
표본 상관계수
모상관계수 (Population Correlation Coefficient)
- 공분산을 표준편차의 곱으로 나누는 것이다.
- 표준화된 공분산을 두 변량 X와 Y사이의 모상관계수 ρ라고 한다.
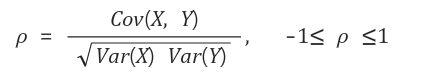
피어슨 상관계수 (Pearson’s Correlation Coefficient)
- 현실적으로 X, Y를 나타내는 두 모집단을 전부 고려하여 모상관계수를 산출하는 경우는 드물다.
- 보통 이변량 모집단으로부터 n개의 임의표본을 추출하여 얻은 X와 Y의 표본 상관계수 r을 사용하며, 이로부터 모 상관계수 ρ를 추정한다. 이 표본 상관계수를 피어슨 상관계수라고 한다.
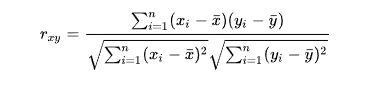
n개의 샘플에 대한 피어슨 상관계수이다.
표본상관계수의 성질
- 표본상관계수 r은 X와 Y사이의 직선 관계가 어느 정도인지를 나타내는 특성치이다.
- 표본상관계수 r의 범위는 -1 ≤ r ≤ 1 이다.
- r = 0이면 두 변량은 무상관이다.
- 0 < r < 1이면 두 변량은 양의 상관이 있다고 하고, r이 1에 가까울수록 강한 양의 상관관계를 갖는다.
- 1- < r < 0이면 두 변량은 음의 상관이 있다고 하고, r이 -1에 가까울수록 강한 음의 상관관계를 갖는다.
- r=1 이면 두 변량은 양의 완전 상관이 있다고 하고, r=-1 이면 두 변량은 음의 완전 상관 있다고 한다.
상관계수의 검정
무상관의 검정
- 이변량 정규 모집단을 구성하는 두 변수 X, Y사이에 상관관계가 존재하지 않는다는 의미의 다음 귀무가설을 검정해보자.
H_0 : ρ = 0
- 이 검정을 무상관 검정 이라고 한다.
- 하는 이유
- 안전성 검사를 예시로 위험으로 부터 무상관 이란것을 알기 위해
무상관의 검정 절차

