이동평균(Moving Average)이란

데이터가 방향성을 가지고 움직일 때, 이동하면서 구해지는 평균을 뜻합니다.

동적으로 변화하는 것에는 어디든 이동평균을 적용할 수 있으며, 또한 1차원적인 방향성을 가지고 이동하기에 이동편균을 적용 가능합니다

단순이동평균(Simple Moving Average, SMA)

가정 m일의 평균(m = Window)

n번째 데이터의 단순 이동평균 = 1번째 데이터를 포함하여 나머지 m개의 데이터의 산술평균

e.g.

• Data = [1, 1, 5, 11, 6, 7]
• n = 1, m = 3

1. 첫 번째 SMA (n=1부터 시작):
   데이터: [1, 1, 5]
   SMA = (1 + 1 + 5) / 3 = 7 / 3 ≈ 2.33
2. 두 번째 SMA:
   데이터: [1, 5, 11]
   SMA = (1 + 5 + 11) / 3 = 17 / 3 ≈ 5.67
3. 세 번째 SMA:
   데이터: [5, 11, 6]
   SMA = (5 + 11 + 6) / 3 = 22 / 3 ≈ 7.33
4. 네 번째 SMA:
   데이터: [11, 6, 7]
   SMA = (11 + 6 + 7) / 3 = 24 / 3 = 8

결과:
[2.33, 5.67, 7.33, 8]

• 실제 계산 방법
  • (이전의 이동평균) + (들어온 가장 최신의 값 - 나간 가장 오래된 값)/m

누적이동 평균(Cumulative moving average, CMA)

단순이동 평균과 같이 산술평균을 구하는 방법이지만 window(m값)을 고정하지 않습니다. (모든 데이터를 고려하고 싶을 때 사용)

새로운 값이 들어올때마다 전체 평균을 새롭게 구하는 것과 동일

• n 번 째 데이터의 누적이동평균 = n번째 데이터를 포함한, 이전 모든 데이터의 평균

e.g.

• Data = [1, 1, 5, 11, 6, 7]
• n = 1
  • 1
• n = 2
  • (1 + 1) / 2

계산식

n + 1 번째 이동평균 = (n번째 누적이동평균 * n + 새로운 데이터 값) / (n + 1)

• 최신 데이터가 현재 상황을 더 잘 반영해 준다면 해당 방식을 차용

(선형)가중이동평균(Weighted moving average, WMA)

데이터의 위치에 따라 서로 다른 가중치를 부여한 후 이동평균을 계산방식 입니다.

• 계산 방식

A = dot product([m, m-1, m-2, …. , 1], [ n번째 데이터, n - 1번째 데이터ㅡ, … , n-m+1번째 데이터])

B = m + (m -1) + … + 1

n번째 데이터의 선형가중이동평균 = A / B

• 오래된 데이터로 갈 수록 곱해지는 값이 선형적으로 감소합니다

지수가중이동평균(Exponentially weighted moving average, EWMA)

선형가중이동평균 지수적으로 감소하는 가중치를 곱해 주는 것

• 계산 방식

A = dot product( [ 1 , (1 - α) , (1 - α)^2 , ... , (1 - α)^(m-1) ],  [n번째 데이터, n-1번째 데이터, ... , n-m+1번째 데이터] )

B = 1 + (1 - α) + (1 - α)^2+ ... + (1 - α)^(m-1)

n번째 데이터의 지수가중이동평균 = A / B

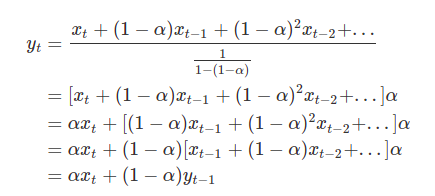
현재의 지수가중이동평균은 바로 이전의 데이터의 지수가중이동평균을 이용하여 구할 수 있습니다.

1번째 지수가중이동평균 = 1번째 데이터 값

n번째 지수가중이동평균 = (1 - α ) (n-1번째 지수가중평균) + α 현재 데이터값

가장 오래된 데이터부터 시작해서 재귀적으로 가장 최근의 데이터까지 지수가중이동평균을 구할 수 있으며, 새로운 데이터가 추가되어도 재귀적을 바로 구할 수 있다.

이 때, α 값은 세가지 방식 중 하나로 구해집니다.

---

작성 진행 중