이상치(Outliers)란?
- 데이터에서 일반적인 패턴, 분포에서 벗어나 극단적으로 크거나 작은 값을 의미한다.
- 이상치는 데이터를 수집할 때에 실수나 오류로 인한 이상한 값일 수도 있는데, 이러한 이상치는 실제 데이터의 특징을 제대로 반영하지 않을 수 있다. (예: 센서 오류, 측정 장비 결함, 데이터 입력 실수)
- 혹은 정확히 수집은 되었지만 특정 분석이나 모델의 학습에 도움이 되지 않는 튀는 값일 수도 있다. 이러한 이상치는 모델이 일반적인 패턴을 학습하는 데 방해가 될 수 있다.
- 이상치를 올바르게 처리하면 모델의 성능을 향상시키고 결과의 신뢰도를 높이는 데 기여할 수 있다.
이상치 식별하기
- 이상치를 식별하기 위해서는 먼저 데이터를 어떤 방식으로 수집했고, 왜 이런 패턴을 띄고 있는지 이해해야 한다. 데이터의 분야(도메인)에 대한 지식이 필요할 수도 있고, 데이터 분석의 목적이나 모델의 특성에 따라 이상치를 판단할 수도 있다.
- 이상치는 주로 통계적 방법이나 데이터를 시각화해서 식별할 수 있다.
- 시각화: Boxplot, 히스토그램, QQ plot 등
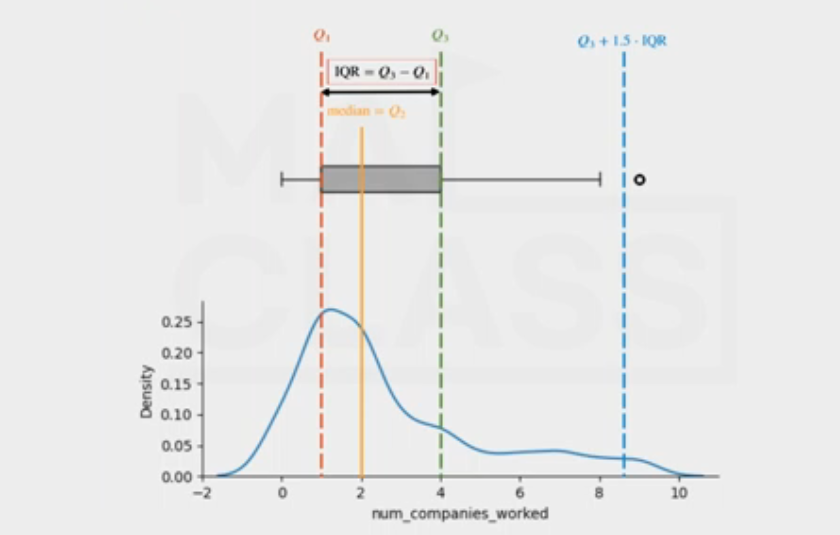
- IQR 범위 활용
- IQR이란 데이터 집합에서 제 1사분위수(Q1)에서 제 3사분위수(Q3)를 뺀 범위를 나타낸다. 이는 데이터 분포의 중간 50%에 해당하는 범위로, 이 범위 안에 포함되지 않는 값들을 이상치로 간주할 수 있다.
- IQR을 구하기
- 데이터 정렬하기
- 제 1사분위수(Q1)와 제 3사분위수(Q3)를 계산
- IQR = Q3 - Q1.
- 코드 예시
- 시각화
- 시각화
# Boxplot으로 분포 시각화하기
fig, ax = plt.subplots(figsize=(8,3))
ax.boxplot([df["working_hours"],df["salary"], df["last_year_salary"], df["num_companies_worked"]])
ax.set_xticklabels(["working_hours", "salary","last_year_salary","num_companies_worked"]) 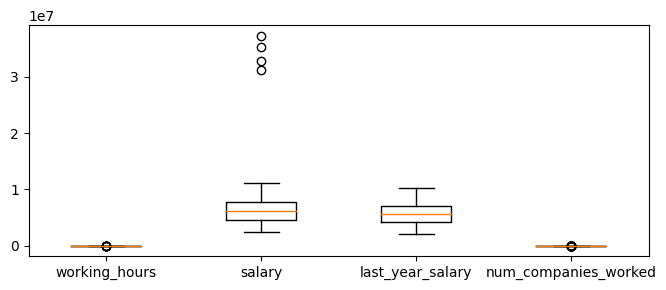
# 변수 간에 수치 차이가 크기 때문에 한 눈에 보기 어려움. -> 분리해서 보자
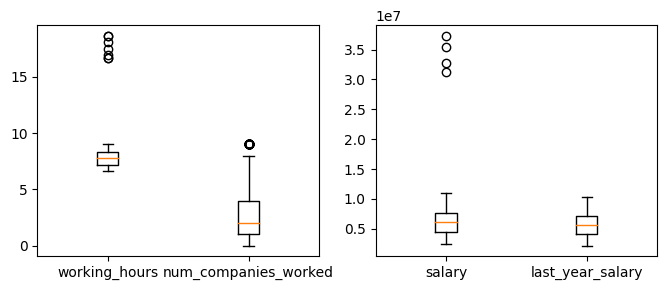
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (8, 3))
ax1.boxplot([df["working_hours"],df["num_companies_worked"]])
ax1.set_xticklabels(["working_hours", "num_companies_worked"])
ax2.boxplot([df["salary"], df["last_year_salary"]])
ax2.set_xticklabels(["salary", "last_year_salary"])
#working_hours와 salary는 각 데이터 분포에 비해 상당히 멀리 떨어져 있음. #num_companies_worked는 상대적으로 가깝게 분포해있지만 일부 outliers로 의심되는 데이터 포인트들이 있음. 직접 눈으로 확인해보기!
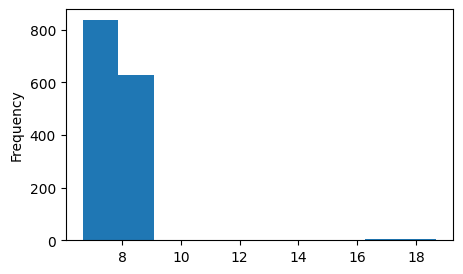
# histogram
"""working_hours"""
fig, ax = plt.subplots(figsize = (5,3))
df["working_hours"].plot(kind="hist", ax = ax)
# 큰 값부터 작은 값으로 나열한 뒤, 상위 10개만 뽑기print(df["working_hours"].sort_values(ascending=False).head(10))
# 상위 7개의 index만 저장하기 -> 나중에 drop하거나 대체할 수 있음.
working_hours_top_idx = df["working_hours"].sort_values(ascending=False).head(7).index
- IQR(InterQuartile) 범위
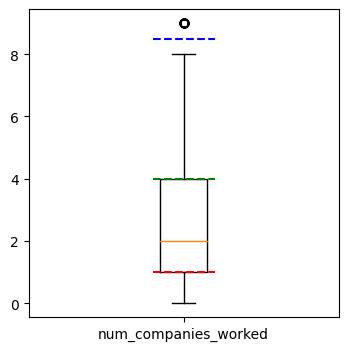
q1 = np.quantile(df["num_companies_worked"], 0.25) # 1분위 값
q2 = np.quantile(df["num_companies_worked"], 0.50) # 2분위 값
q3 = np.quantile(df["num_companies_worked"], 0.75) # 3분위 값
iqr = q3 - q1
fig, ax = plt.subplots(figsize = (4,4))
ax.boxplot(df["num_companies_worked"])
ax.set_xticklabels(["num_companies_worked"])
ax.plot([0.9,1.1], [q1, q1], c = "red", linestyle="--")
ax.plot([0.9,1.1], [q3, q3], c = "green", linestyle="--")
ax.plot([0.9,1.1], [q3+1.5*iqr, q3+1.5*iqr], c = "blue", linestyle="--")
# 1.5를 늘리면 iqr 범위를 더 넉넉하게 가져갈 수 있음. (정상 분포라고 여겨지는 범위를 늘리는 것-> outlier는 더 줄어들것)
# 이 파란 점선을 넘어가는 친구들을 outlier 후보라고 볼 수 있음.
# matplotlib - boxplot의 노란 선은 중앙값을 의미한다.
# iqr 범위에서 벗어난 데이터 추출
outliers =
df[(df["num_companies_worked"] < q1 - 1.5 * iqr) | (df["num_companies_worked"] > q3 + 1.5 * iqr)]
outliers
이상치 처리하기
- 제거하기
- 대체하기
- Numerical
- 평균(Mean)이나 중앙값(Median) 이용
- Trimmed Mean - 특정 백분위수를 제외한 Trimmed 평균 사용하기
- Categorical
- Numerical
- Scaling
- 이상치에 강건한 모델 선택하기
Reference
- 예시는 (MathAI)나민원 박사님의 데이터 전처리 및 모델 성능 평가 강의를 참고합니다.
