스티커 모으기(2) [python]

N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.
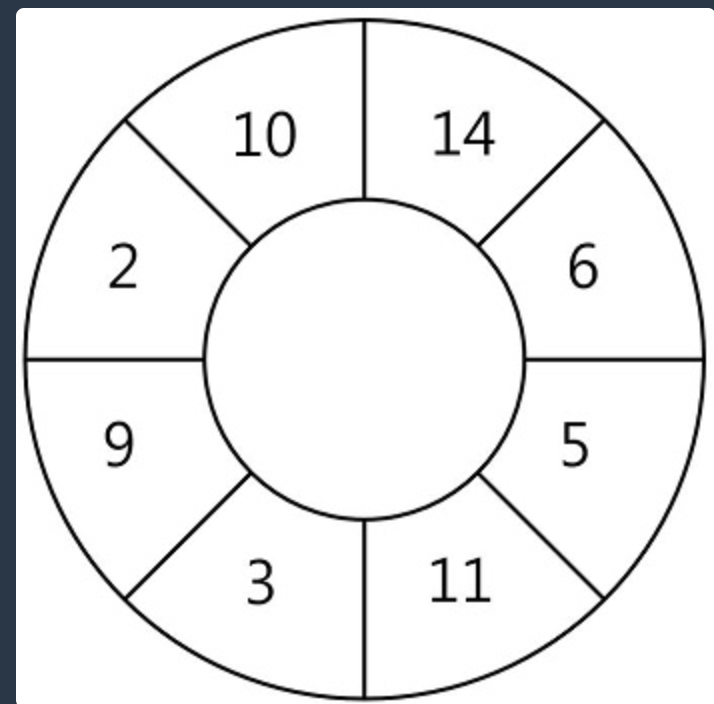원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.

예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.

제한 사항

• sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
• sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
• 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

입출력 예
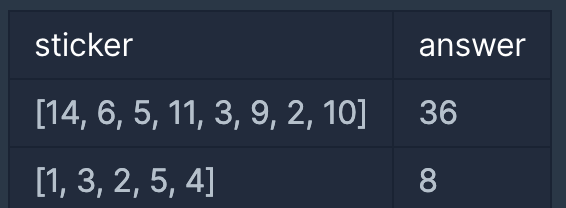
sticker answer

입출력 예 설명

입출력 예 #1
6, 11, 9, 10이 적힌 스티커를 떼어 냈을 때 36으로 최대가 됩니다.

입출력 예 #2
3, 5가 적힌 스티커를 떼어 냈을 때 8로 최대가 됩니다.

누가봐도 dp로 풀어야겠다는 생각이 강하게 든다.
하지만 여기서 고민을 한 것이 처음과 끝을 어떻게 잇지..? 라는 생각이다.
하지만 잇는 것이 아니다. 잘 생각해보면 잇는다는 것은 시작점을 내가 새로 정해야 한다는 것인데, 그렇다면 이을 필요가 없지 않는가

하나를 선택하면 선택하지 못하는 숫자의 갯수가 일정하다. 2개
즉, 이것을 이용하는 것인데, 이 문제의 핵심은 내가 숫자를 골라서 합을 구하는 것이 아니다. 모든 경우의 합을 구해서 최대값을 뽑아 내는 것이다.

1. 내가 14를 선택하면 6은 절대 선택하지 못한다. 그렇다면 6에서의 최대값은 14.

2. 5에서의 최대값은 14 + 5(5를 뽑는다면) 혹은 6에서의 최대값(14, 5를 뽑지 않는다면)이다. 이런식으로 해결해 나가는 것이다.

3. 또한 첫번째 원소를 뽑냐 안뽑냐를 나눠서 계산하고 그 중에 최대값을 구한다. (첫 번째 원소를 뽑으면 마지막 원소를 절대 뽑지 못하기 때문이다)
   dp 어렵다...

def solution(sticker):
    s_num = len(sticker)
    if s_num == 1:
        return sticker[0]
    ## 첫번째 원소를 뽑는 경우
    pointer = [0]*s_num
    pointer[0] = sticker[0]
    pointer[1] = pointer[0]
    for i in range(2, s_num-1):
        pointer[i] = max(pointer[i-1], pointer[i-2]+sticker[i])
    val1 = max(pointer)
    
    ## 첫번째 원소를 뽑지 않는 경우
    pointer = [0]*s_num
    pointer[1] = sticker[1]
    for i in range(2, s_num):
        pointer[i] = max(pointer[i-1], pointer[i-2]+sticker[i])
    val2 = max(pointer)

    return max(val1, val2)