기초통계 003 - 기술 통계 (1)

기술 통계

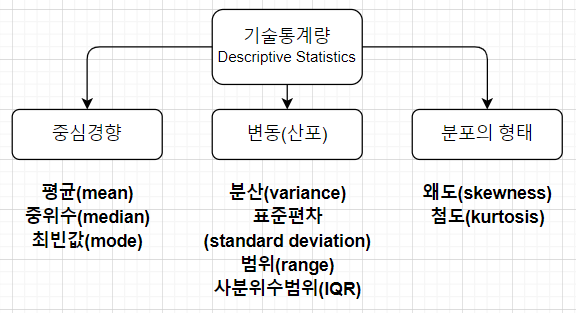
중심경향 (대표값)

• 평균 - Outlier에 민감

  $\bar X = \frac{1}{n} \cdot \sum_{i=1}^{n}x_i$

BigQuery에서는 AVG() 집계함수를 이용하여 쉽게 평균을 구할 수 있다.

DECLARE sample ARRAY<INT64> DEFAULT [2, 2, 1, 3, 2, 9, 30];
SELECT AVG(s) AS avg FROM UNNEST(sample) s;

• 중위수/중앙값
  • 정렬된 자료에서 중앙에 위치한 값 (짝수일 경우 가운데 2개의 평균)
  • 이상치(outlier)에 강건
    

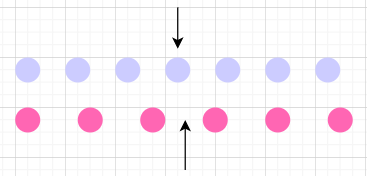
BigQuery는 MEDIAN()함수를 지원하지 않는다. 대신 다음의 방법을 통해서 중앙값을 구할 수 있다. 여기서 PERCENTILE_DISC(s, p)와 PERCENTILE_CONT(s, p)는 분석함수로서 주어진 s 컬럼이 정렬된 상태에서의 누적비율이 p에 해당하는 값을 리턴한다.
s 컬럼을 이산형(discrete) 변수로 볼 것인지 연속형(continuous) 변수로 볼 것인지에 따라 계산되는 값이 달라짐을 볼 수 있다.

DECLARE sample ARRAY<INT64> DEFAULT [42, 57, 68, 75, 86, 92];

SELECT PERCENTILE_DISC(s, 0.5) OVER () median_d,
       PERCENTILE_CONT(s, 0.5) OVER () median_c
  FROM UNNEST(sample) s LIMIT 1;

Row	median_d	median_c
1	68	71.5

참고로 PERCENTILE_DISC()나 PERCENTILE_CONT()는 분석함수(윈도우함수)이므로 OVER() 구문과 어울려 사용되고 있으며 집계함수와 달리 각 행별로 결과를 만들기 때문에 LIMIT 1을 사용하여 동일한 결과가 반복적으로 출력되는 것을 방지하였다.

• 최빈값
  • 빈도가 가장 많은 관측값. 유일하지 않을 수 있으며 존재하지 않을 수도 있다.

DECLARE sample1 ARRAY<INT64> DEFAULT [1, 2, 3, 4, 5, 6, 7];
DECLARE sample2 ARRAY<INT64> DEFAULT [1, 2, 3, 3, 3, 6, 7, 7, 7, 8, 9];
DECLARE sample3 ARRAY<INT64> DEFAULT [1, 3, 5, 7, 9, 9, 9, 9, 10];

WITH sample0 AS (
  SELECT s, COUNT(*) OVER (PARTITION BY s) mode
    FROM UNNEST(sample2) s
   WHERE TRUE QUALIFY COUNT(*) OVER (PARTITION BY s) > 1
)
SELECT DISTINCT s 
  FROM sample0
 WHERE TRUE QUALIFY RANK() OVER (ORDER BY mode DESC) = 1

Row	s
1	3
2	7

모든 관측값이 서로 다를 경우 최빈값이 구해지지 않으므로 sample0 서브쿼리에서 COUNT() 분석함수(집계함수아님)를 이용하여 필터링하고 있다.

다음 메인쿼리에서는 앞선 서브쿼리에서 계산한 각 관측값의 빈도수를 바탕으로 순위를 매겨 가장 높은 빈도수의 관측값을 남긴다. 이 때 동일한 빈도수의 관측값이 여러 개가 존재할 수 있으므로 ROW_NUMBER()가 아닌 RANK() 함수를 사용해야 한다.

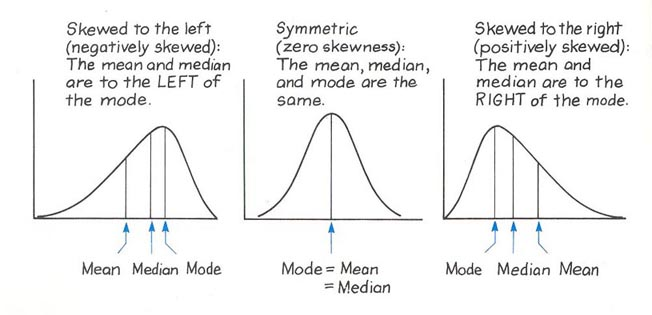
[출처] http://webbuild1.knu.ac.kr/~bskim/normality.htm

기타

• 평균이 중앙값, 최빈값보다 많이 사용되는 이유
  • 계산의 용이성
  • 평균은 수식으로 계산 가능한 반면 중앙값, 최빈값은 전체 데이터를 스캔해야 함.
• 데이터의 분포가 대칭형일 경우 평균으로 충분. 쌍봉분포, 이상치등을 포함한 경우에는 중앙값, 최빈값을 같이 제시