Graph; MST (ing)

JP·2022년 11월 13일

TIL

인접행렬(방향, 무방향)

(방향) 행은 시작 인덱스, 열은 도착 인덱스; 0->1 이면 arr[0] = 1
(무방향) symmetric. diagonal은 전부 0.

인접리스트(linked list)

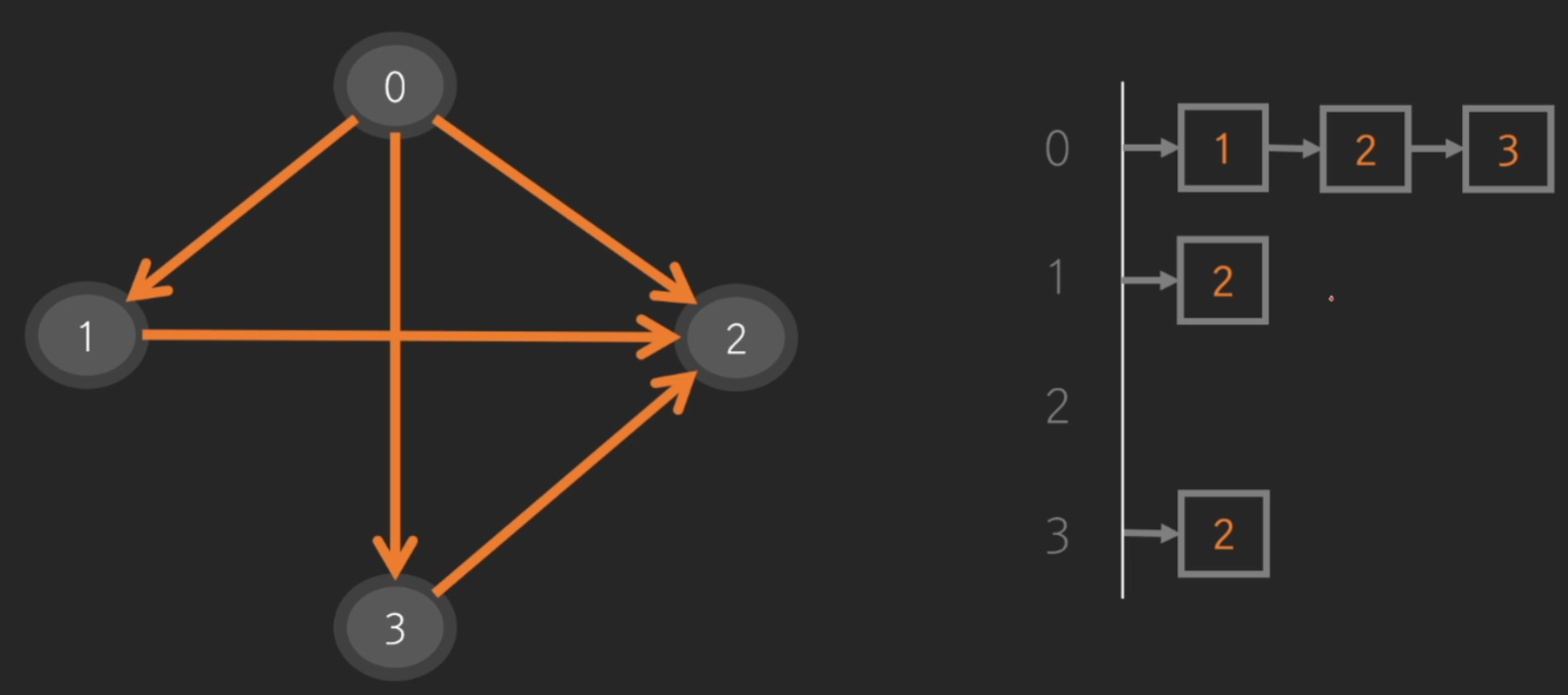
메모리 관점에서, '인접리스트'가 유리함. 대신 arr[0][3]에 접근하고 싶을 때는 상황이 다름. 인접리스트는 O(N) 걸림.

Spanning Tree

그래프에서 모든 vertex 에 대해 최소한의 연결만 남긴 그래프를 일컬음. vertex가 n개라면, edge 수는 (n-1).

MST(minimum ST)

edge의 가중치 합이 가장 작은 트리.

이런 트리를 구해내는 알고리즘의 종류에는

크루스칼 알고리즘(Kruskal's algorithm)
- O(ElogV)
프림 알고리즘(Prim's algorithm)
- 큐 이용 시 O((V+E)logV)
등이 있다.

그래프의 vertex 밀도에 따라 시간복잡도가 상이하기에, 조건에 맞게 알고리즘을 택해야 함.
그럼 크루스칼 알고리즘부터 좀 헤쳐보자.

Kruskal's Algorithm

Greedy method 기반의 알고리즘. 이전 단계에서 만든 ST와 무관하게, 항상 최소값 edge만 선택.

증명

- (왜 해당 알고리즘으로 MST를 구할 수 있는지; TBC;)

동작

가중치를 오름차순 정렬
사이클을 형성하지 않는 선에서, 계속 선택
선택한 edge를 MST집합에 추가

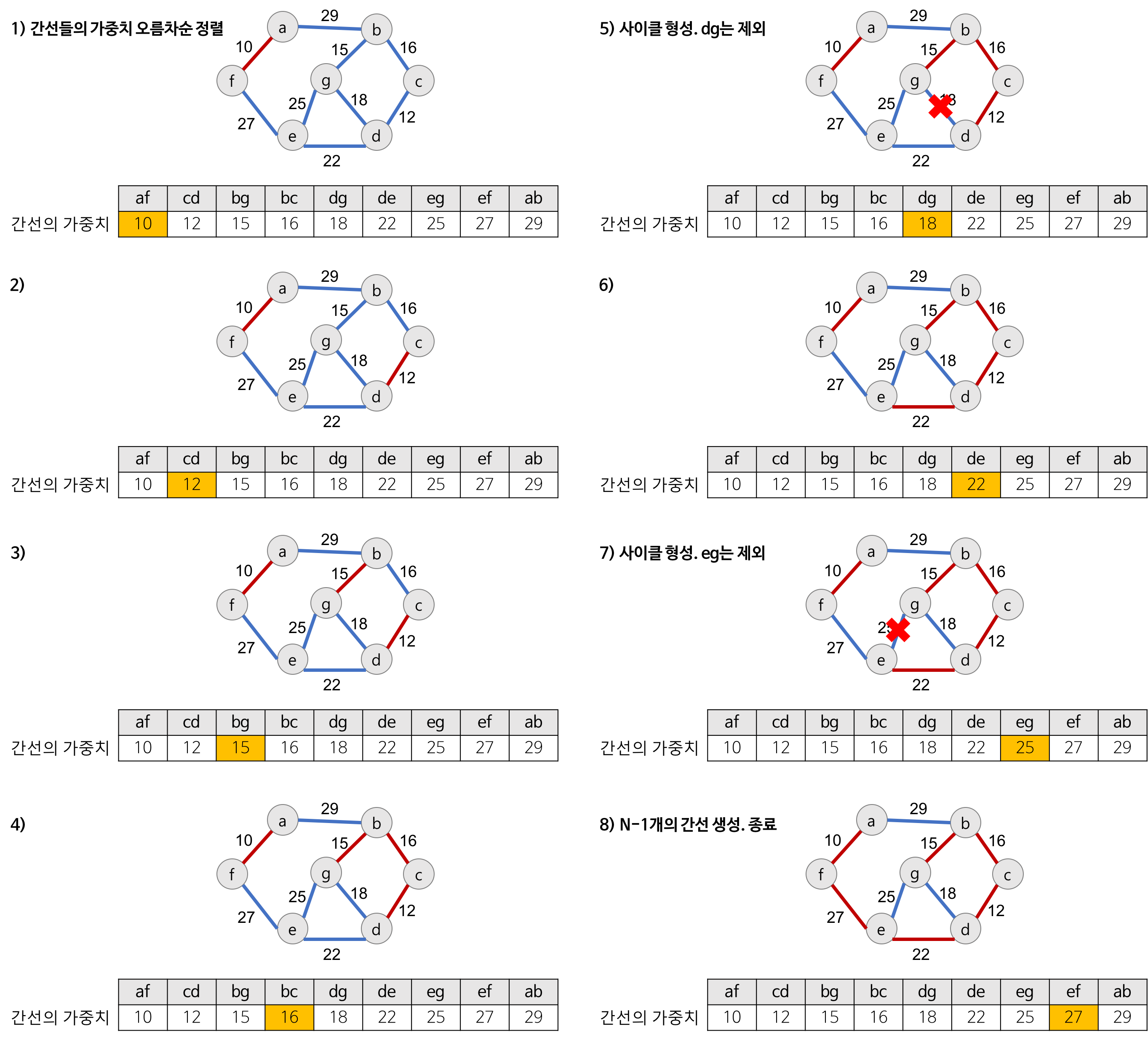
(출처: https://gmlwjd9405.github.io/2018/08/29/algorithm-kruskal-mst.html)

사이클 생성 여부
- 추가하려는 edge 양끝이 '같은 집합(루트 노드가 같은지)'에 속해있는지 검사
- union-find 알고리즘 이용

구현

import sys

v, e = map(int, input().split())
# 부모 테이블 초기화
parent = [0] * (v+1)
for i in range(1, v+1):
    parent[i] = i

# find 연산
def find_parent(parent, x):
    if parent[x] != x:
        parent[x] = find_parent(parent, parent[x])
    return parent[x]

# union 연산
def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

# 간선 정보 담을 리스트와 최소 신장 트리 계산 변수 정의
edges = []
total_cost = 0

# 간선 정보 주어지고 비용을 기준으로 정렬
for _ in range(e):
    a, b, cost = map(int, input().split())
    edges.append((cost, a, b))

# 간선 정보 비용 기준으로 오름차순 정렬
edges.sort()

# 간선 정보 하나씩 확인하면서 크루스칼 알고리즘 수행
for i in range(e):
    cost, a, b = edges[i]
    # find 연산 후, 부모노드 다르면 사이클 발생 X으므로 union 연산 수행 -> 최소 신장 트리에 포함!
    if find_parent(parent, a) != find_parent(parent, b):
        union_parent(parent, a, b)
        total_cost += cost

print(total_cost)