aka 서로소 집합 알고리즘; disjoint-set algorithm;

연산

• make-set(x): 초기화. x를 유일 원소로 하는 집합 만들기.
• union(x,y): x가 속한 집합 + y가 속한 집합.
• find(x): x가 속한 집합의 대표(루트 노드 값)값을 반환.

구현

'트리 구조'를 이용.

1. 배열의 경우,

• make-set(x)
  arr[i] = i처럼 각자 다른 집합 번호로 초기화
• union(x,y)
  배열 모든 원소를 순회하며, y의 집합번호를 x의 집합번호로 변경
  시간 복잡도가 O(N)
• find(x)
  시간 복잡도 O(1)

2. 트리를 쓰면,

• 같은 집합 = 하나의 트리. 따라서 집합번호 = 루트 노드
• make-set(x)
  N개의 루트 노드 생성. 자기 자신으로 초기화
• union(x,y)
  x, y의 루트 노드 찾고, 다르면 y를 x의 자손으로 넣어, 두 트리 합친다.
  시간복잡도가 O(N)보다 작음
• find(x)
  루트 노드를 확인해서 같은 집합인지 확인.
  시간 복잡도가 최악일 때 O(N-1)임. 트리 높이랑 동일.

예시

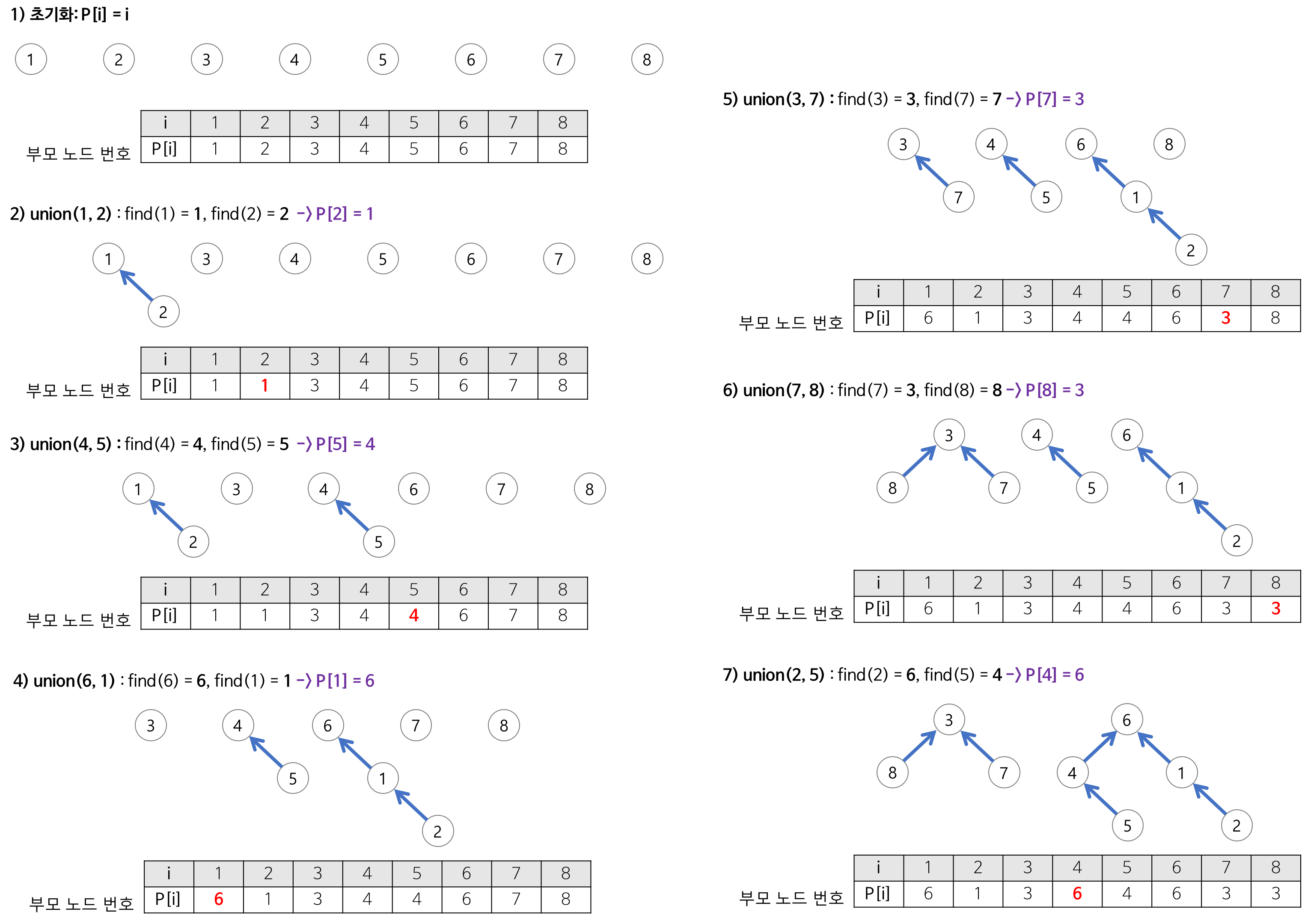
전체 집합에서, 원소들이 겹치지 않게 분할할 때 자주 사용.

# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
    # 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if parent[x] != x:
        return find_parent(parent, parent[x])
    return x

# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b: # 숫자가 작은 녀석이 부모가 됨
        parent[b] = a
    else:
        parent[a] = b

# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화하기

# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
    parent[i] = i

# Union 연산을 각각 수행
for i in range(e):
    a, b = map(int, input().split())
    union_parent(parent, a, b)

# 각 원소가 속한 집합 출력하기
print('각 원소가 속한 집합: ', end='')
for i in range(1, v + 1):
    print(find_parent(parent, i), end=' ')

print()

# 부모 테이블 내용 출력하기
print('부모 테이블: ', end='')
for i in range(1, v + 1):
    print(parent[i], end=' ')

위 알고리즘을 '최적화'할 수도 있단다.
최적화가 필요한 이유로는, 깊이가 깊은 다음과 같은 예시때문인데,

• 5->4->3->2->1
  이 때 5의 루트노드를 찾으려면 O(V)의 시간복잡도가 발생된다.
  따라서 '경로 압축'의 최적화를 통해 find 함수를 손 볼 수 있다.

# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
    # 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if parent[x] != x:
        return find_parent(parent, parent[x])
    return parent[x] # 리턴 값만 수정

뭐가 달라지겠냐만은, 부모테이블을 출력해보면

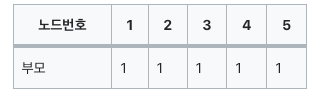
다음과 같아지면서 루트노드에 빠르게 접근할 수 있다.