[알고리즘] RE:재귀 호출

재귀호출

함수가 자기자신을 호출하는 것을 재귀호출이라고 한다.

수학적 귀납법

모든 자연수 n에 대하여 n! <= nn임을 증명하시오.

1. N = 1일 때 성립함을 보인다.

2. P(k)가 성립한다고 가정할 때, P(k+1)이 성립함을 보인다.

3. 따라서 모든 자연수 n에 대하여 P(n)이 성립한다.

def factorial(n):
    if n == 0:
        return 1
    else:
        return factorial(n-1) * n

퀵 정렬(Quick sort)

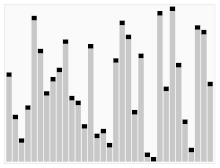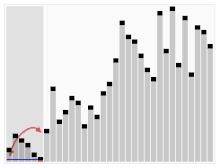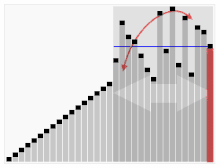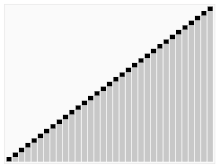
퀵 정렬은 재귀 호출을 이용한 대표적인 정렬이다. 피봇을 가운데에 두고 피봇보다 작은값을 왼쪽에 큰값을 오른쪽에 둔다.

Quick Sort (Array a, pivot p)

Step 1: p 를 a에서 랜덤하게 설정, 배열의 왼쪽 끝과 오른쪽 끝의 인덱스를 i, j로 설정
Step 2: p < i 이고 p > j 이면 i와 j를 교환하고 i 와 j 위치를 이동한다.
Step 3: p > i 이고 p > j 이면 i위치를 p보다 큰 값이 나올 때까지 이동한다.
Step 4: p < i 이고 p < j 이면 j위치를 p보다 작은 값이 나올 때까지 이동한다.
Step 5: i > j 이면 Step 7 로 이동한다.
Step 6: Step 2로 이동
Step 7: p를 기준으로 좌우 리스트에 대해 재귀적으로 수행

Complexity

Name	Best	Average	Worst	Memory	Stable
Quick sort	n log(n)	n log(n)	n2	log(n)	No

퀵 정렬 구현해보기

def quickSort(data):
    if len(data) <= 1:
        return data
    pivot = data[0]

    left = getSmallNumbers(data[1:], pivot)
    right = getLargeNumbers(data[1:], pivot)

    return quickSort(left) + [pivot] + quickSort(right)

def getSmallNumbers(data, pivot):
    l = []
    for elem in data:
        if elem <= pivot:
            l.append(elem)
    return l

def getLargeNumbers(data, pivot):
    l = []
    for elem in data:
        if elem > pivot:
            l.append(elem)
    return l

재귀함수 디자인하기

재귀함수를 디자인하기 위한 세가지 단계

1. 함수의 정의를 명확하게 한다.

2. n = 1에서 함수가 제대로 동작하게 작성한다.

3. P(n)에 대하여 P(n-1)가 제대로 동작한다고 가정하고 함수를 완성한다.

Ex1 옳은 괄호인지 확인하기

예를 들어 '(())'은 올바른 괄호이지만 '(()))', 혹은 '(()()('는 올바른 괄호가 아니다.

def checkParen(data):
    if len(data) == 0:
        return True
    elif len(data) == 1:
        return False
    if data[0] != "(":
        return False
    for idx, a in enumerate(data):
        if a == ")":
            data2 = data[:idx-1] + data[idx+1:]
            return checkParen(data2)
    return False