먼저 앞서 배웠던 BST에서는 큰 문제가 하나 있었다. 그것은 최악의 경우 수행시간이 O(n)이 되는 것이다. 그것을 해결하기 위한 Tree는 바로 RBT이다.
RBT의 루트는 블랙이다.
모든 리프(NIL)는 블랙이고
노드가 레드이면 그 노드의 자식은 반드시 블랙이다(RED-RED 불가)
루트 노드에서 임의의 리프 노드에 이르는 경로에서 만나는 블랙 노드의 수는 모두 같다.
이러한 성질을 가진 트리를 코드를 구현하기 이전에 먼저 보기 쉬운 알고리즘으로 정리하였다.
삽입 알고리즘
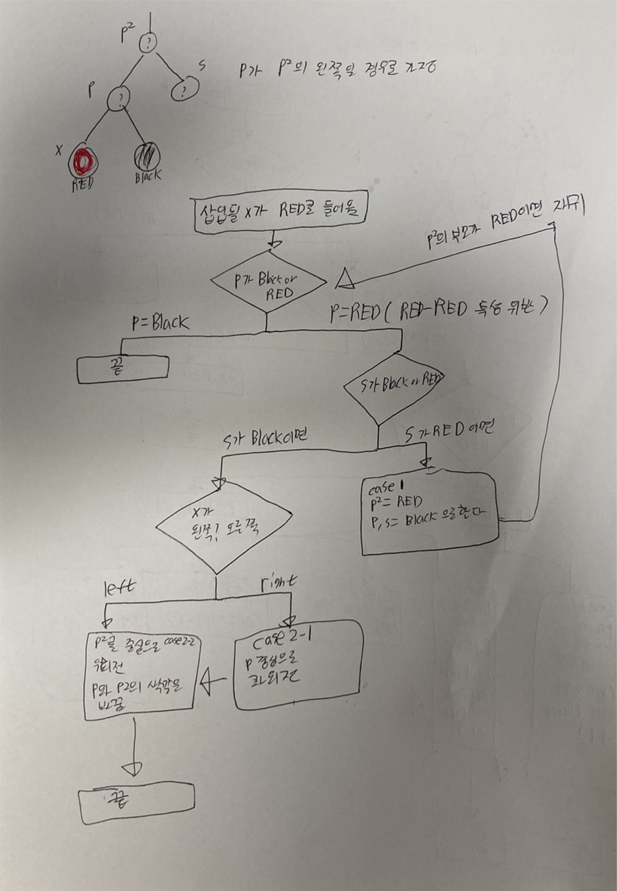
이것은 RBT에서 이루어지는 삽입 알고리즘을 보기 쉽게 표현한 것이다.
Search기능은 BST와 매우 흡사하기 때문에 레포트에는 기록하지 않았다.
1. x가 RED로 들어오고 그 부모의 따라서 나뉘게 된다. BLACK이라면 특성을 위반하지 않기 때문에 RED일 때만 보면 된다.
2. p가 레드 일때 s의 색깔에 따라서 또 나뉘게 된다. S가 RED라면 단순히 그 보이는 자리에서 특성을 만족하게 하고 그 위에가 RED라면 전체적으로 특성을 위반하기 때문에 다시 재귀적으로 차차 맞추어 간다
3.S가 BLACK이라면 x가 왼쪽에 있거나 오른쪽에 있음에 따라 나뉘게 된다.
4.오른쪽이라면 p를 중심으로 좌회전 한다. 그렇게 되면 x가 왼쪽에 있는 case의 상황이 되기 때문에 그 케이스로 가게 된다.
5. 그리고 p2을 중심으로 우회전한다.
6.마지막으로 p와 p2의 색상을 바꾸게 되면 삽입이 끝나게 된다.
우회전, 좌회전
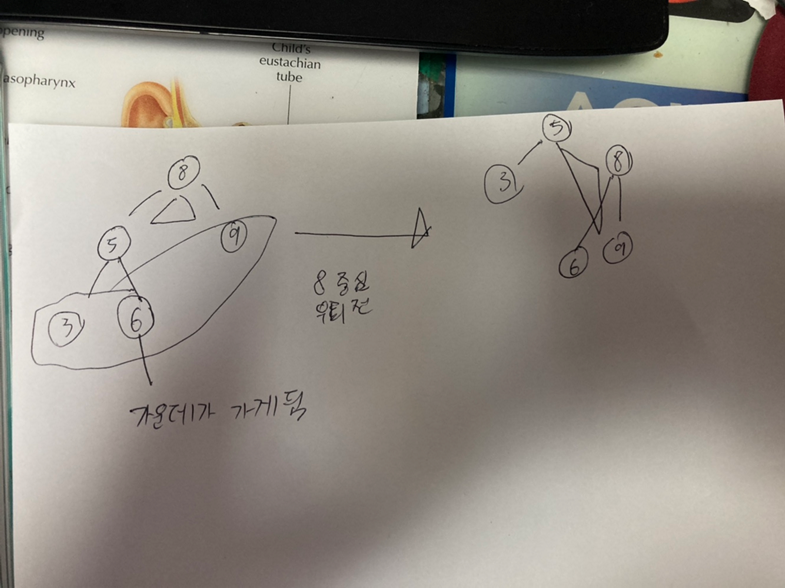
앞에서 삽입 알고리즘을 설명할 때 우회전, 좌회전이라는 단어를 사용했다. 그것은 왼쪽 사진 처럼 진행되는 것이다.
왼쪽은 우회전이고 노드의 좌회전은 반대로 진행하면 된다.
삭제 알고리즘
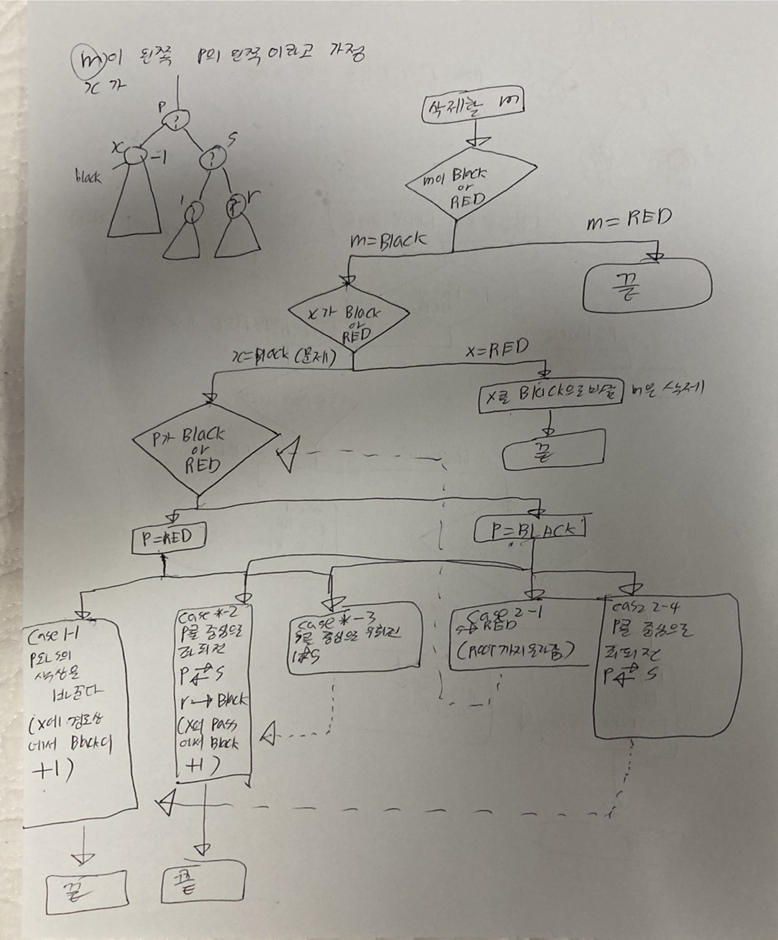
다음으로는 삭제 알고리즘을 살펴 보겠다.
이 역시 기본적으로 BST의 삭제가 기반이 된다.
1.삭제할 m이 들어오면 m이 BLACK or RED로 경우의 수가 나뉘게 된다. RED라면 BLACK의 개수를 위반하지 않기 때문에 문제가 없다
2.m이 BLACK일 때만 보자. M이 BLACK이라면 그 자식의 색깔이 중요하다. 자식의 색깔이 BLACK이냐 RED이냐에 따라 또 갈리게 된다. 그 자식 노드가 RED라면 또 BLACK의 개수에 문제가 없기 때문에 아주 쉽게 마무리가 된다.
3.x가 BLACK이라면 삭제 후 경로상 BLACK이 -1이 되므로 문제가 발생한다.
4.그때는 또 x의 부모인 p의 색깔로 나뉘게 된다.
p=RED일 때
Case 1-1
Case -2
Case -3 -> case -2
p=BLACK일 때
Case -2
Case -3 -> case-2
Case 2-1 ->재귀
Case 2-4 ->case 1-1
이처럼 red일때와 black일 때 경우의 수가 겹치게 된다.
이 말은 즉 겹치는 case는 p의 색깔이 어떻든 같은 알고리즘을
수행 한다는 말이 된다.
이렇게 여러 케이스를 거쳐서 삭제할 노드 뺴고 나머지 부분을 연결하며 RBT의 특성을 맞추게 된다.
CreateNode 함수
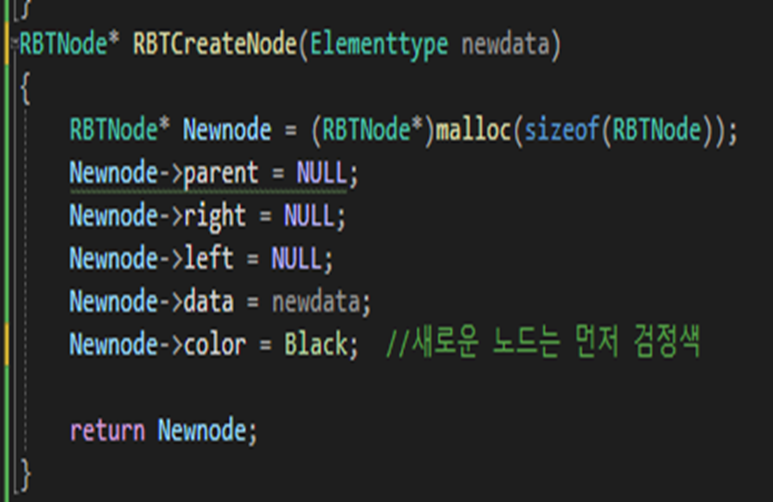
이제 직접 구현한 코드를 분석하겠다.
코드를 구현하고 매 줄마다 주석을 달면서 코드를 분석하였다
CreateNode함수는 새로운 노드를 만드는 함수이다.
BST와 다르게 paren를 NULL로 지정하고 color라는 변수가 있다
새로운 노드의 색깔은 검정색으로 시작한다.
RBTInsertNode

말그대로 삽입 함수이다.
BST처럼 삽입을 진행 후 그 삽입 노드의 색깔을 레드로 바꾼다.
그리고 RBT의 특성을 따라 BLACK 리프를 달아준다
그리고 리빌드를 해준다.
RBTInsertNodeHelper
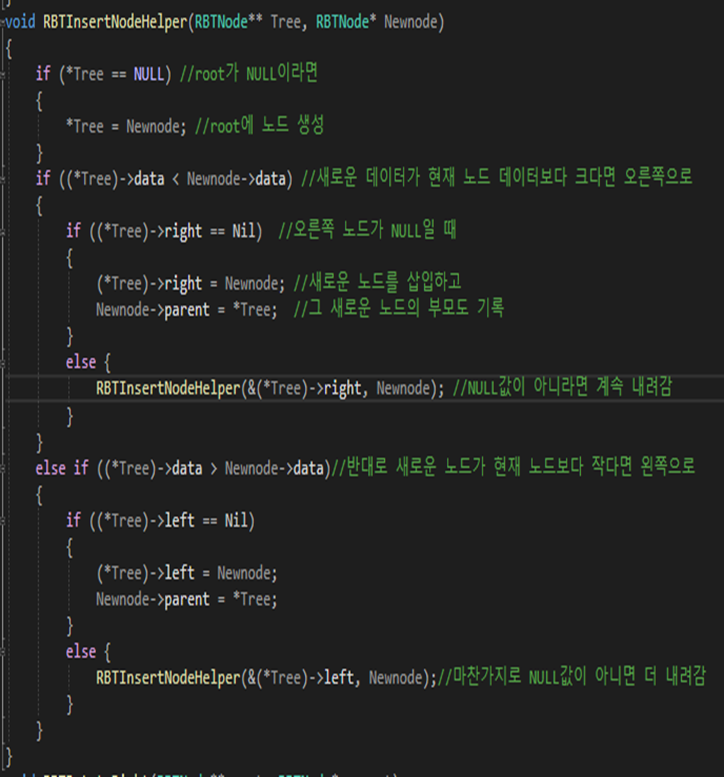
이 함수는 BST에서 보았던 삽입 과정과 똑같다.
RBTRebuildAfterInsert 함수
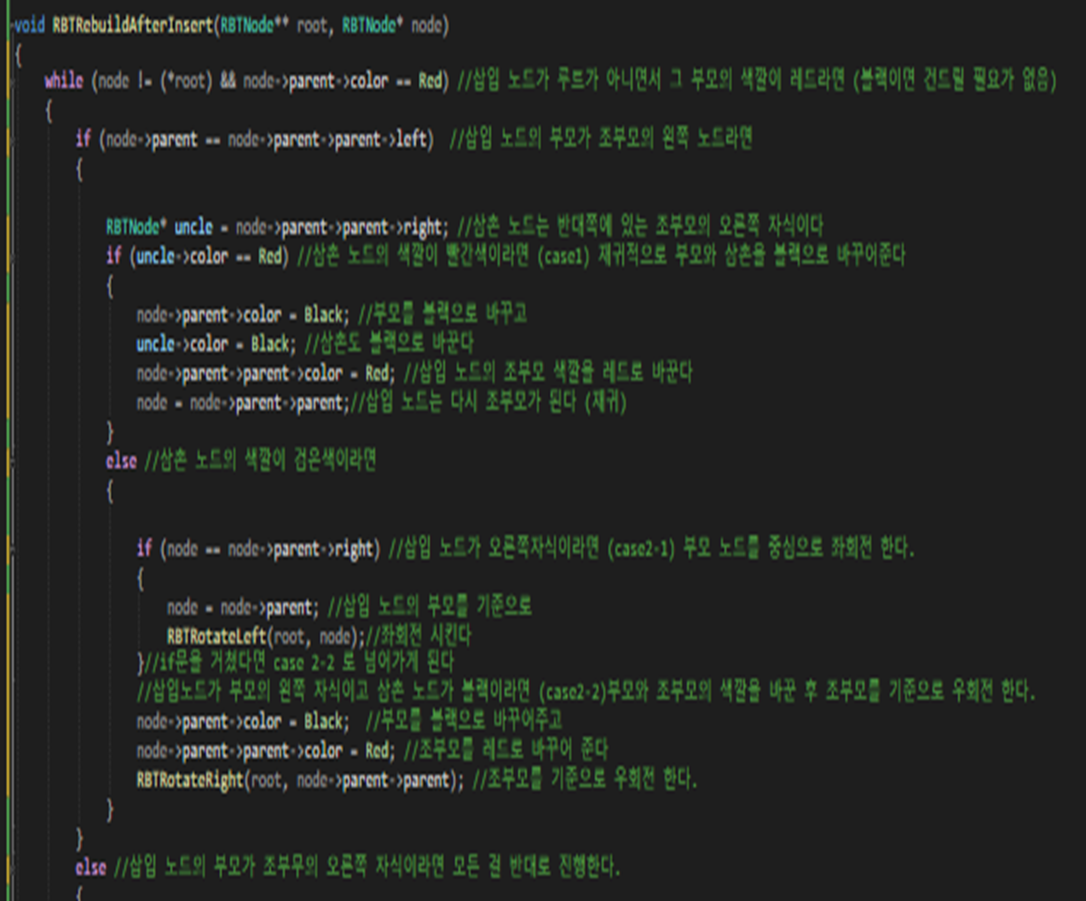
이 함수는 삽입된 노드가 특성에 위반되지 않게 앞서 보았던 케이스 알고리즘을 코드로 구현한 함수이다.
Case1의 재귀
Case2-1의 좌회전 후
Case2-2로 가서 우회전하고
조부모와 부모의 색깔을 맞바꾸는 과정까지
잘 구현되어 있다.
그리고 마지막으로 반대 케이스는
모든 걸 반대로 구현했기 때문에 사진의 크기 상
생략했다.
RBTRemove
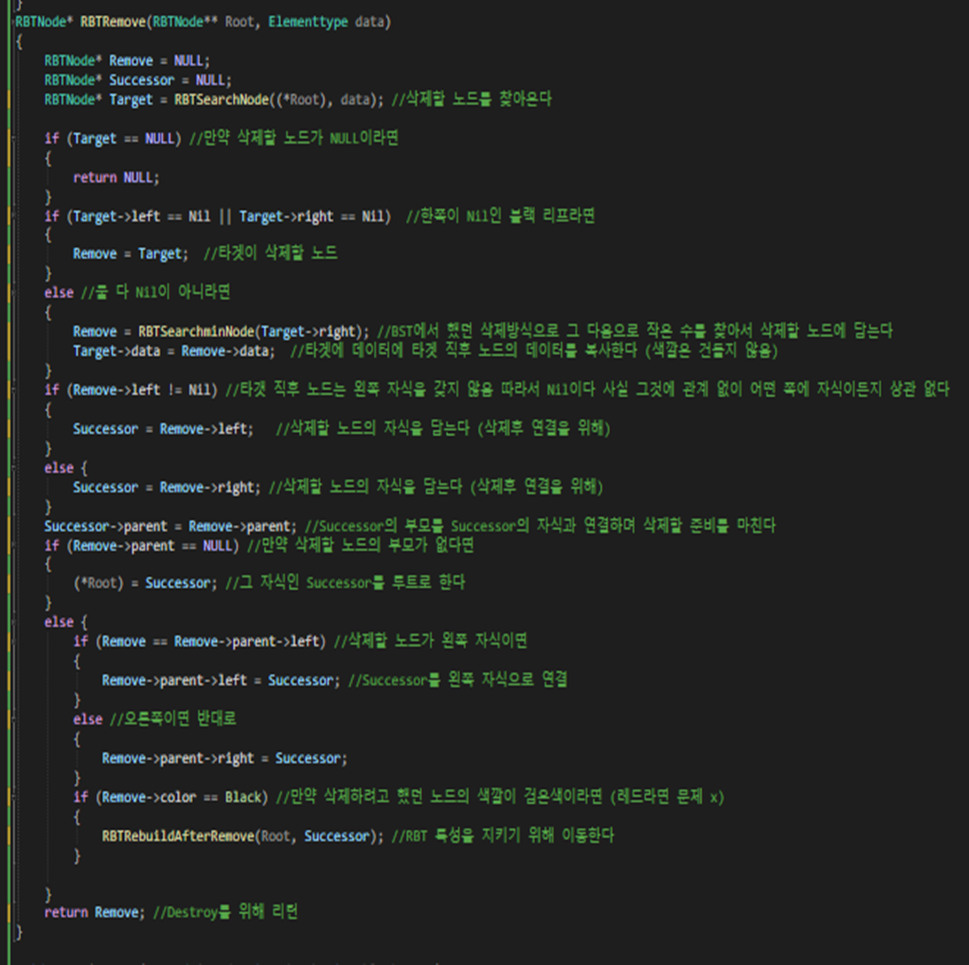
이 함수는 BST의 삭제의 기능을 기반으로 구현한 REMOVE 함수이다. Successor를 구하고 RBT 특성을
지키기 위해서 삽입과 마찬가지로 리빌드 함수로 특성을 지켜낸다.
RBTRebuideAfterRemove 함수
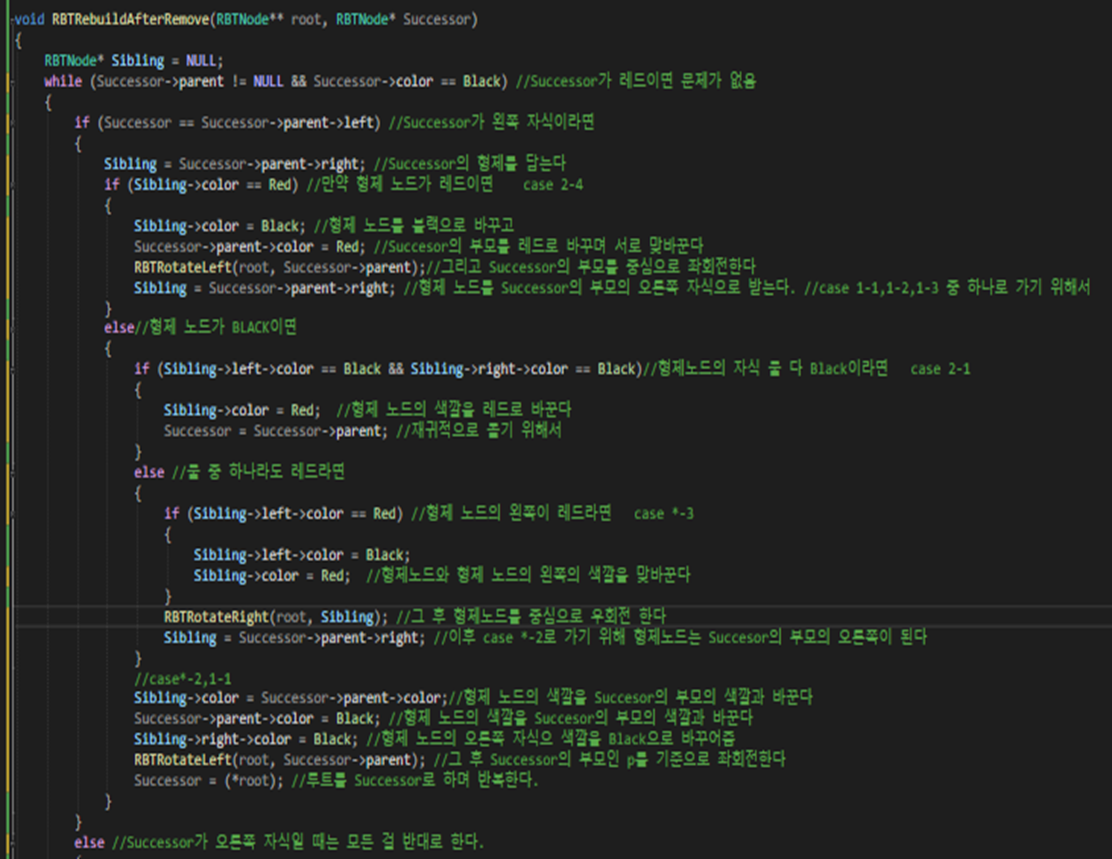
이 함수는 함수를 리무브 결정하고 받은
Successor를 이용하여서 RBT가
특성을 위반하지 않게 하기 위해 리빌드 하는
과정이 담긴 함수이다.
앞서 보인 내가 직접 그린 알고리즘
과는 다른 순서이지만 case가 하나도
빠짐 없이 잘 구현되어 있다.
Case 2-4 ->case 1-1
Case 2-1 -> 재귀
Case -3 ->case-2

