- 이진 탐색 트리란 정렬된 이진트리로써 다음과 같은 속성을 가지고 있다.
- 노드의 왼쪽 하위 트리에는 노드의 키보다 작은 키가있는 노드 만 포함된다
- 노드의 오른쪽 하위 트리에는 노드의 키보다 큰 키가있는 노드 만 포함된다.
- 왼쪽 및 오른쪽 하위 트리도 각각 이진 검색 트리 여야한다.
- 중복된 키를 허용하지 않는다.
BST의 시간 복잡도
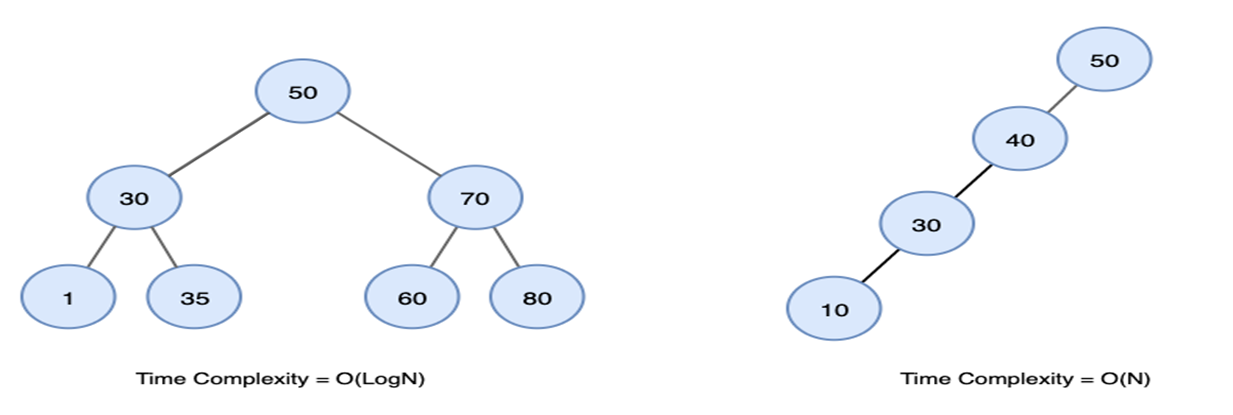
BST는 위 왼쪽 그림 처럼 평균적인 이진 트리의 구조를 가질 때에는 매 탐색 때마다 반으로 나뉘기 때문에 O(logN)의 시간 복잡도를 갖게 된다.
하지만 오른쪽 경우 처럼 한 쪽으로 편향된 구조를 갖게 된 이진 트리라면 배열에서 탐색하는 것과 다르지 않기 때문에 O(N)의 시간 복잡도를 가지게 된다.
노드의 구조

이제 내가 BST에서 삽입,검색,삭제 기능을 구현한 코드를 분석해보겠다.
먼저 트리를 구성하는 노드의 구조를 보겠다
트리는 배열을 사용하게 되면 불필요한 메모리를 너무 많이 사용하기 때문에 연결리스트의 구조를 사용하게 된다.
그렇기에 각 노드는 data인 key값과 왼쪽 자식 오른쪽 자식을 담을 수 있는 공간을 부여 받는다.
연결리스트를 사용하면 비어 있는 인덱스를 사용하지 않을 수 있고 부모가 그 다음 자식의 주소를 기억하는 구조이기 때문에 삽입과 삭제가 매우 깔끔하고 간편하다.
Main 함수
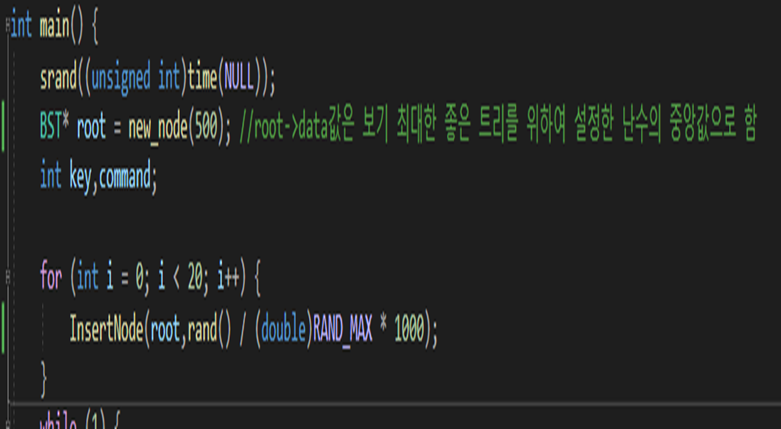
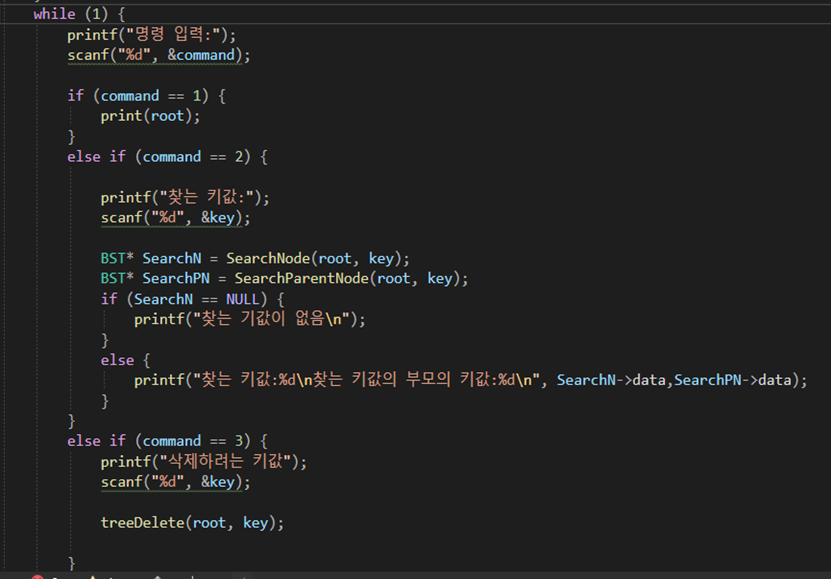
위 코드들은 main함수의 코드들이다. 난수를 발생 시켜서 이진트리의 노드를 만들었다. Root노드의 키값은 난수의 범위중 중앙을 설정하여 높은 확률로 좋은 모양의 트리가 나오게 하였다.
여기서 new_node함수를 이용하여 새로운 노드를 만들고 InsertNode로 적절한 위치에 노드를 삽입했다. 그리고 각각 커맨드 명령으로 중위순환,검색,삭제 기능을 구현했다.
New Node함수와 InsertNode함수


먼저 InsertNode에서 삽입하려는 key값의 위치를 정해주었다. 부모보다 key값이 작으면 왼쪽 크면 오른쪽의 구조이기 때문에 쉽게 찾아갈 수 있다.
그 이후에 자식 값이 없게 되면 그 곳이 삽입 위치이기 때문에 new_node함수로 새로운 노드를 만들어주면서 삽입하게 된다.
New_node에서 새로운 노드이기 때문에 자식은 NULL로 초기화 해준다
SearchNode
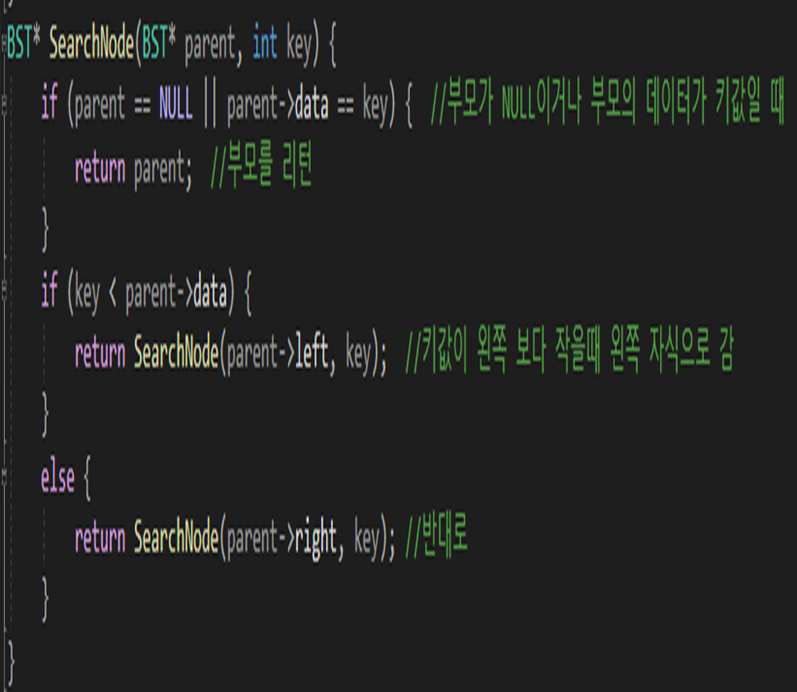
SearchNode함수는 이진 트리에서 원하는 키값의 노드를 찾는 함수이다. 이진 트리의 구조에 맞게 작은 수는 왼쪽 크다면 부모의 오른쪽으로 내려가는데 내려가다보면 키값과 같은 데이터의 노드를 찾게되면서 그 노드를 리턴해준다.
중위 순환

순환의 종류에는 전위 순환, 중위 순환, 후위 순환이 있다.
이번 코드에서는 작은 수부터 출력되어 알아보기 쉽게 하기위해 중위 순환으로 출력했다.
왼쪽 노드 부모 노드 오른쪽 노드 순으로 출력해주었다.
Search,print함수 실행 화면
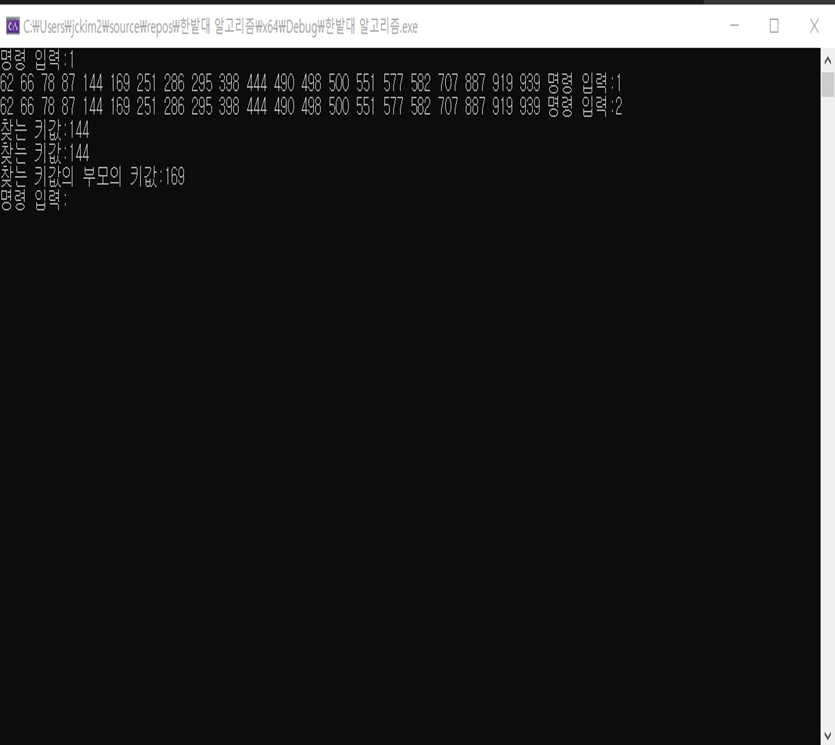
이는 1번 커맨드 (print)를 실행한 화면이다 중위 순환이기 때문에 작은 값부터 출력되는 것을 볼 수 있다.
그 다음은 2번 커맨드(SearchNode)를 실행하였다. 144번 키 값을 검색했더니 역시 144번 키 값이 나오게 되었다.
추가적으로 삭제할 때 필요하기에 그 노드의 부모를 찾는 함수도 추가했다.
부모 노드를 검색
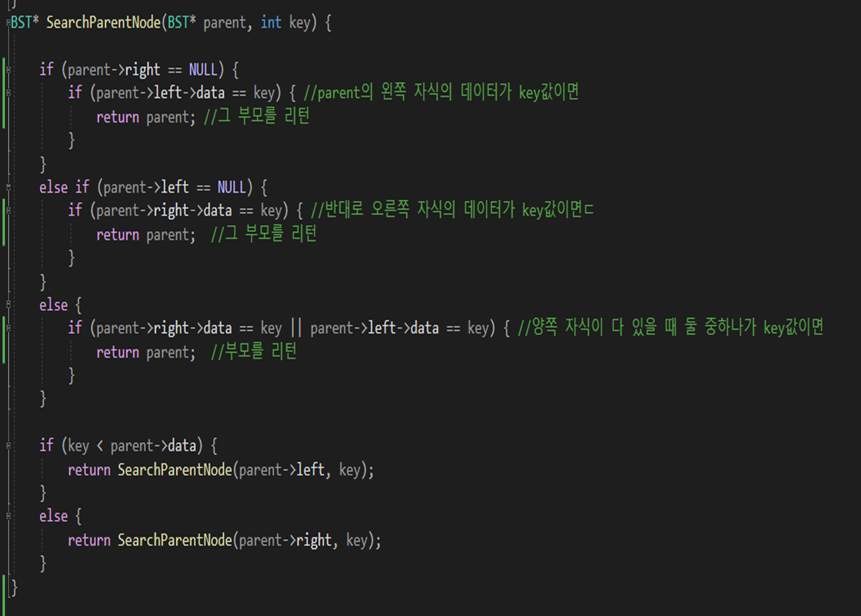
이 코드는 앞서 말한 삭제를 하기 위해 필요한 해당 노드의 부모 노드를 찾는 함수 이다. 원래 검색 함수와 다른 점은 그 자식들 중 하나가 key 값이라면 현재의 부모를 리턴 하는 함수로 구현하였다.
한 단계 이전에서 리턴 하는 것이다.
DeleteNode 함수
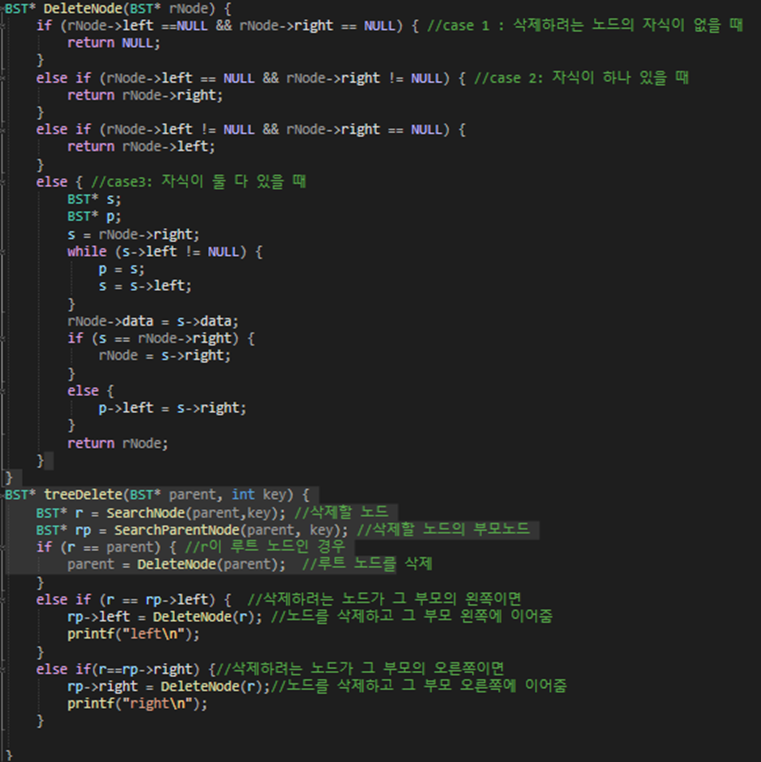
이 함수는 해당 키값의 노드를 삭제하는 함수 이다. 먼저 treeDelete로 삭제 노드가 루트 노드 인 경우를 걸러준다. 그리고 삭제하려는 노드를 그 다음 큰 수와 바꾸기 때문에 어떤 자리의 이어줄지 정해야한다. 그렇기 때문에 삭제 노드의 부모의 왼쪽에 이어야할 지 오른쪽에 이어야할 지 정해준다. 정했으면 DeleteNode를 호출 한다. DeleteNode에 대해서 그 다음 장에서 보겠다.
노드의 삭제
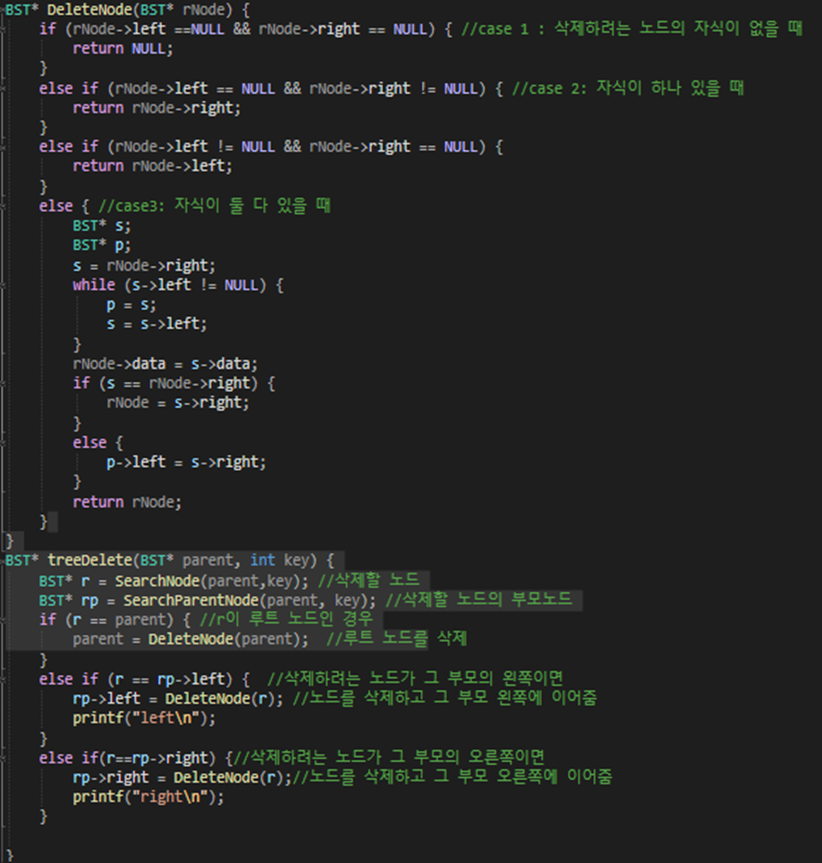
노드의 삭제에는 3가지 경우의 수가 있다.
Case1은 삭제하려는 노드의 자식이 없을때 case2는 하나의 자식만 있을 때 case3는 두개의 자식이 있을 때다.
먼저 case1은 그 노드만 삭제해주면 된다. Case2는 삭제하려는 노드가 그 부모의 왼쪽 자식인지 오른쪽 자식인지 판별하고 삭제 후 적절한 위치에 삭제 노드의 자식을 이어준다.
Case3는 먼저 해당 노드를 삭제하고 그 삭제 노드보다 다음으로 큰 수를 찾는다. 그 다음 그 큰 수를 원래 삭제 자리에 이어주고 그 큰 수의 자식을 적절하게 이어주면 이진 검색 트리의 구조를 유지할 수 있다.
Delete 함수 실행 화면
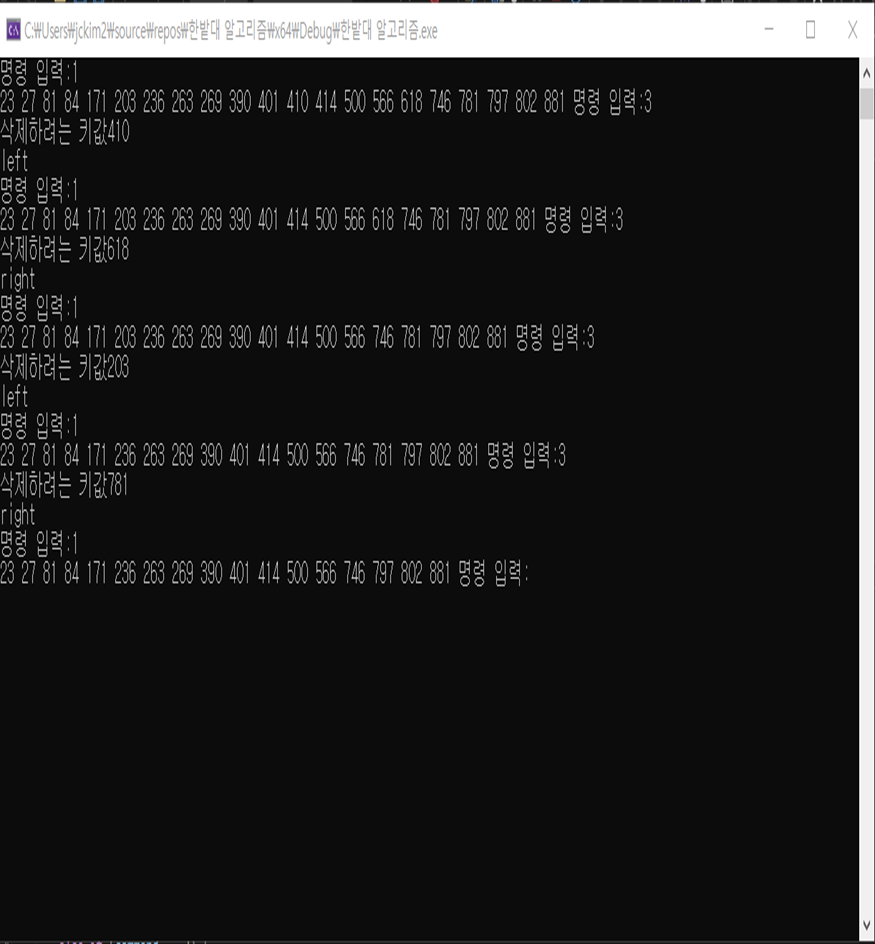
옆 캡처 화면과 같이 500(root의 키값)을 기준으로 왼쪽은 left 오른쪽은 right가 출력되게 했고 처음에 410을 삭제하고 차례로 618, 208, 781을 삭제하는 결과를 볼 수 있다
부모 노드가 필요없는 Delete방식
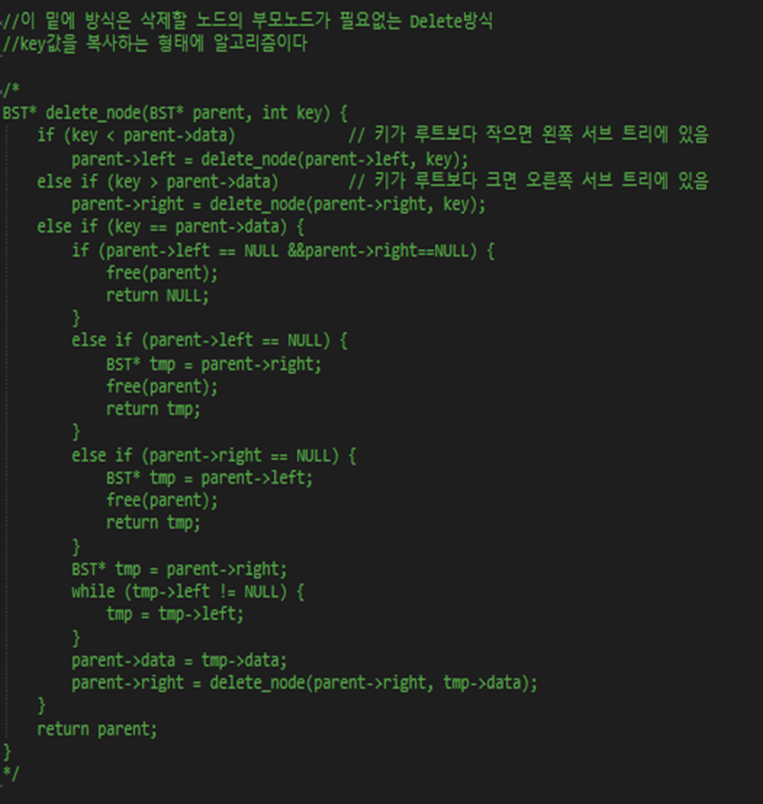
더 공부해보다 보게 된 알고리즘이다. 삭제 노드의 부모 노드를 구하지 않아도 되어서 보다 깔끔한 코드를 구현할 수 있다. 하지만 노드 자체를 옮기는 것이 아닌 키 값을 복사하는 것이기 때문에 키 값 이외에 데이터가 많다면 유용하지 않을 수 있을 것 같다.
Free함수를 사용하여서 노드를 완벽하게 삭제하는 것을 볼 수 있다.

