분할 정복 알고리즘 이란?
그리디 알고리즘에 들어가기 앞서 비교 학습을 위해 분할 정복 알고리즘에 대해서 잠깐 알아 보았다.
분할 정복 알고리즘이란 주어진 문제의 입력을 분할하여 문제를 해결(정복)하는 방식의 알고리즘 이다. 분할 된 입력에 대하여 동일한 알고리즘을 적용하여 해를 계산하며, 이들의 해를 취합하여 원래 문제의 해를 얻는다.
여기서 분할된 입력에 대한 문제를 부분문제 라고 하고, 부분 문제의 해를 부분해 라고 한다. 부분 문제는 더이상 분할 할 수 없을 때까지 계속 분할 한다.
그리디 알고리즘이란?
Greedy(탐욕) 알고리즘은 말 그대로 순간마다 최적의 선택을 하여 최종적으로 해를 구하는 알고리즘이다.
그리디 알고리즘이 최적의 알고리즘인 문제들은 많이 없다.
순간마다 하는 선택이 최적의 선택일지라도 최종적으로 내는 해답이 가장 최적의 해답이라는 보장이 없기 때문이다.
그러나 그리디 알고리즘이 최종적으로 구하는 해답의 최적이라면 그리디 알고리즘만한 알고리즘이 없다.
그리다 알고리즘 문제 해결 절차
선택 절차: 현재 상태에서의 최적의 해답을 선택한다.
적절성 검사: 선택된 해가 문제의 조건을 만족하는지 검사한다.
해답 검사: 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복한다.
그리디 알고리즘 문제 해결 조건
탐욕적 선택 속성 : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
최적 부분 구조 : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
거스름돈 알고리즘
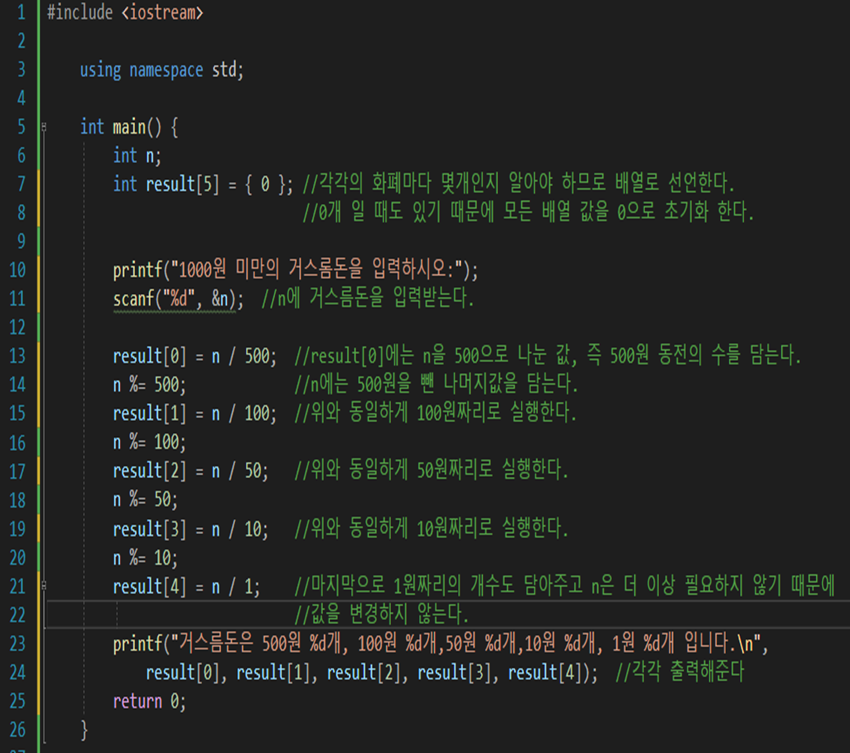
그리디 알고리즘하면 대표적으로 나오는 알고리즘이다.
각각의 화폐의 개수를 적을 배열을 5의 크기로 선언했다.
예시로 721원을 입력했다.
n은 먼저 가장 최적의 해이고 큰 수인 500원 동전을 찾게 된다.(Greedy)
그 이후에 500원 짜리를 뺀 값인 261원을 n에 초기화 해주었다.
그 다음으로 가장 최적의 해 이자 큰 수인 100원을 찾아 개수를 구해주었다.
동일한 방법으로 1원까지 구해주게 되면 그리디 기법을 사용하여 최소의 동전 개수를 구할 수 있다.
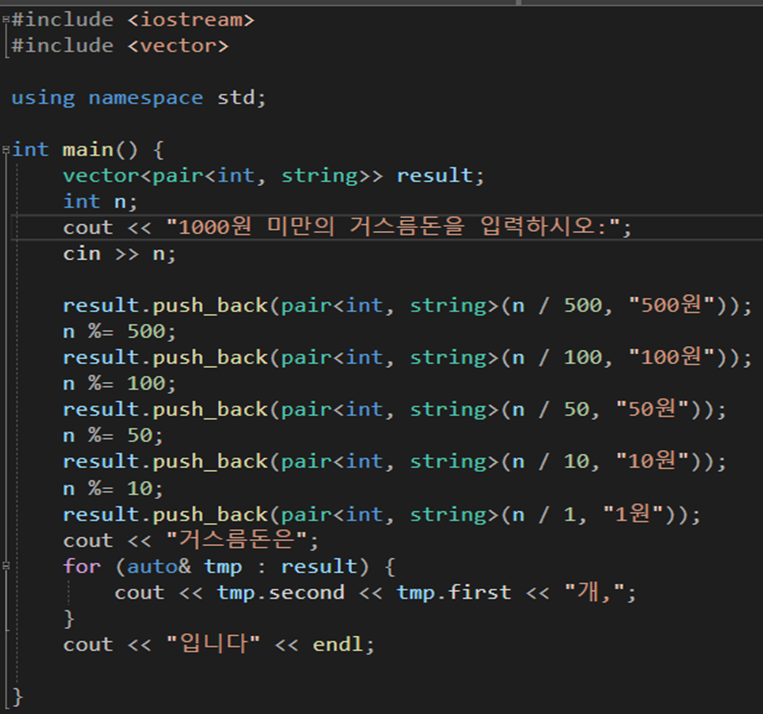
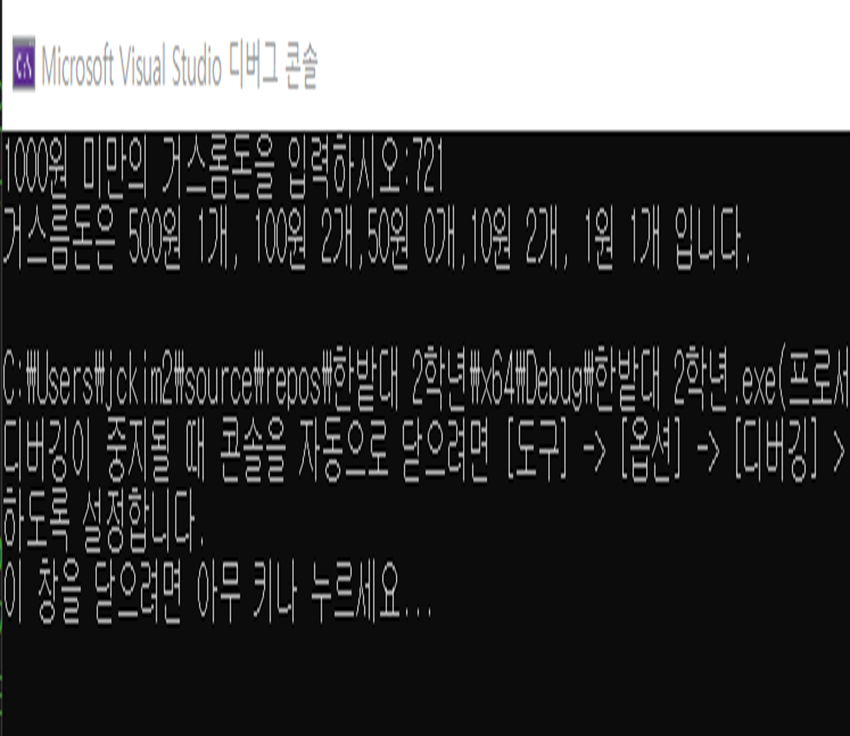
추가적인 공부를 위해 c++문법으로도 코드를 짜보았다.
배열 대신 vector와 pair함수로 result값과 화폐의 이름을 동시에 담아주었다.
그리디 기법으로 C코드 처럼 진행해서 범위기반 for문으로 출력 해주었다.
그리디 알고리즘이 최적해를 구하지 못하는 경우
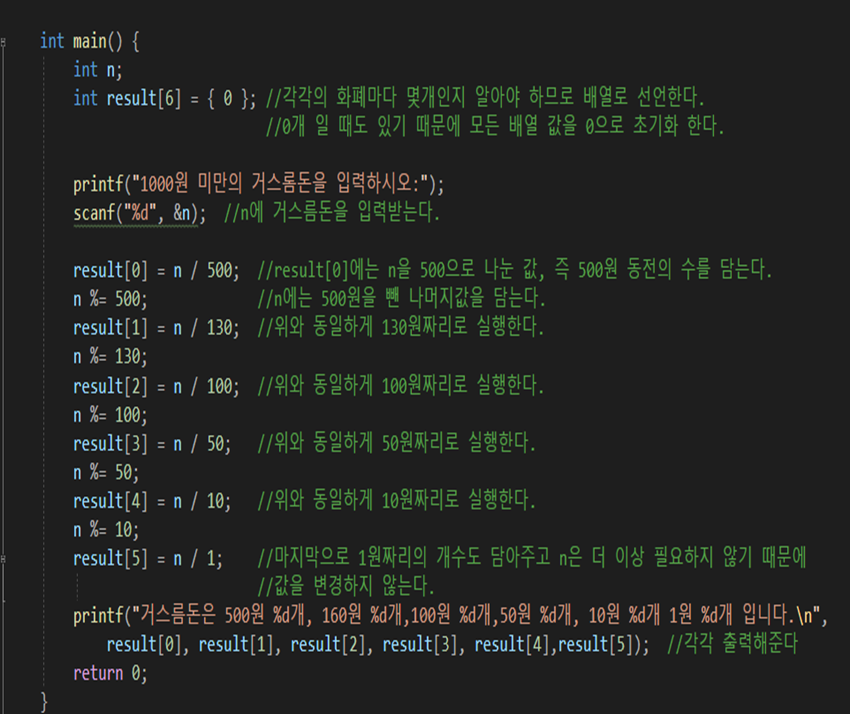
앞서 말했듯이 그리디 알고리즘은 항상 최적의 해를 구할 수 없다.
이건 예시의 상황이다.
130원의 동전이 있다고 가정했을 때, 최적의 해는 5001+1002+102+11 로
6개 이지만 130원의 동전이 있을 때에는 그리디 기법이 8개라고 해를 구한다.
이건 그리디 알고리즘이 최적해를 구하지 못하는 소스의 실행화면이다.
이렇듯 그리디 알고리즘이 최적해를 구하기 위해서는 앞서 말한 조건들이 성립해야 가능하다고 할 수 있다.

