사용한 개념

https://littlefoxdiary.tistory.com/3 (힙큐)
블로그를 참고하였다.

우선순위 큐를 사용하였지만 라이브러리 자체는 힙큐이다.
완전 정렬되어 있는 리스트를 힙에 푸쉬하기 때문에 우선순위 큐랑 동일하게 보고 사용해도 좋다.

첫번째 풀이가 시간 초과가 나서 문제 풀이 또한 블로그를 참고하였다.

첫 시도가 실패한 이유

알고리즘은 구현 했지만 내 알고리즘은 시간 복잡도가 O(n2)이었다.
n<200,000 까지 입력되는 문제에서 시간 복잡도가 O(n2)은 치명적인 문제였다.

따라서 최소 O(nlogn)까지 줄여야 했는데 정렬 함수가 O(nlogn)의 수행시간을 갖고 있었다.

( sort() - 퀵정렬 기반, sorted() - 병합정렬 기반)

결과적으로 우선순위 큐를 다시 복습하고 풀이를 보고 다시 풀어 정렬 제외 O(n)의 알고리즘을 만들었다.

정렬을 포함하면 최종적으로 O(nlogn)의 수행시간이 들었기 때문에 시간 초과 문제를 해결할 수 있었다.

문제

문제 바로가기

수강신청의 마스터 김종혜 선생님에게 새로운 과제가 주어졌다.

김종혜 선생님한테는 Si에 시작해서 Ti에 끝나는 N개의 수업이 주어지는데, 최소의 강의실을 사용해서 모든 수업을 가능하게 해야 한다.

참고로, 수업이 끝난 직후에 다음 수업을 시작할 수 있다. (즉, Ti ≤ Sj 일 경우 i 수업과 j 수업은 같이 들을 수 있다.)

수강신청 대충한 게 찔리면, 선생님을 도와드리자!

입력

첫 번째 줄에 N이 주어진다. (1 ≤ N ≤ 200,000)

이후 N개의 줄에 Si, Ti가 주어진다. (0 ≤ Si < Ti ≤ 109)

출력

강의실의 개수를 출력하라.

예제 입력

3
1 3
2 4
3 5

예제 출력

2

문제 검토

이전 회의실 배정 문제와 비슷하게 끝나는 시간 다음으로 바로 시작 시간을 찾는다는 점에서 그리디 기법을 사용하는데 용이하다고 할 수 있다.

허나 다른 강의실을 개설해 알고리즘을 풀어야 한다는 점에서 너무 직관적으로 들어가게 되면 O(n2)의 알고리즘을 구현하게 될 것이다.

강의실에 수업은 하나만 있어도 강의실의 개수를 유지할 수 있다는 점에 유의해야 한다.

O(n2)의 결과를 피하기 위해 시작 시간 조회를 하는 수행을 빼야한다.
그런 이유로 우선순위 큐를 사용한다는 점에서 우선 순위 큐 문제가 되겠다.

풀이(python)

Python - O(n2)

from sys import stdin

n = int(stdin.readline())

s=[]
cnt=0 

for x in range(n):
    a = list(map(int,stdin.readline().split()))
    s.append(a)


s=sorted(s,key=lambda x:(x[1],x[0]))


cur=s[0][1]

del s[0]

while len(s)>0:
    check=True
    
    for i in range(len(s)):
        if s[i][0]>=cur:
            cur=s[i][1]
            check=False
            del s[i]
            break
    if not check:
        continue
    elif check:
        cnt+=1
        cur=s[0][1]
        del s[0]
        

cnt+=1

print(cnt)
        
        

처음 내가 구현한 알고리즘이다.
알고리즘은 알맞지만 while과 for에서 N인 len(s)를 사용했다는 점에서 O(n2)의 결과를 낳게 된다.

Python - O(nlogn)

from sys import stdin
import heapq

n = int(stdin.readline())

s=[]

for x in range(n):
    a = list(map(int,stdin.readline().split()))
    s.append(a)

s=sorted(s,key=lambda x:x[0])

r = []
heapq.heappush(r,s[0][1]) #첫번째 강의의 끝나는 시간을 큐에 push

for x in range(1,len(s)): #두번째 강의부터 비교
    if s[x][0] < r[0]: #만약 반복문의 비교하는 강의의 시작시간이 현재 큐의 첫번째 강의실 종료시간보다 작다면
        heapq.heappush(r,s[x][1]) #강의실 개설
    else:              #현재 큐의 첫번째 강의실에서 이어서 강의 가능함
        heapq.heappop(r) #큐는 그저 강의실 개수를 측정하기 위함이므로 한 강의실에서 다음 강의가 이어진다면 다음 강의를 pop해준다
        heapq.heappush(r,s[x][1]) #이어지는 강의 푸쉬 다음 반복부터는 다른 강의실 비교 시작
        
print(len(r))

우선순위 큐는 큐의 형태를 하고 있지만, 항상 정렬이 되어 있는 큐를 말한다.
heapq의 특성상 최소힙을 유지하고 있으면 항상 최소값이 첫번째 인자에 있다.

이 문제의 핵심은 조회하는 반복을 없애기 위해 항상 큐에 첫번째 인자를 비교한다는 것이다.

이전 코드에서는 해당 끝나는 강의 시간 다음에 시작하는 시간을 찾기 위해 매번 반복했다.

하지만 이 풀이에서는 큐에 0번째 인덱스의 강의를 유지하여 (1번째 강의실) 다음 강의와 비교하고 다음 강의가 겹친다면 새로운 강의실을 개설한다.(2번째 강의실)

1.강의 리스트를 정렬한다.
2.첫 번째 강의가 끝나는 시간을 우선순위 큐에 추가한다.
3.강의 리스트의 1번째 인덱스부터 마지막까지 반복문을 실행한다

• 3-1.우선순위 큐에 첫 번째 인덱스에 접근한다 (항상 끝나는 시간이 가장 빠른 순)
  3-2.만약 강의의 시작시간이 우선순위 큐의 첫 번째 인덱스보다 작다면 해당 강의의 끝나는 시간을 우선순위 큐에 추가한다.
  3-3.아니라면 우선순위 큐의 첫 번째 인덱스를 pop 한 후 해당 강의의 끝나는 시간을 우선순위 큐에 추가한다.

이렇게 강의실을 왔다갔다하며 O(n)의 반복으로 강의실의 개수를 파악한다.

아래 사진은

4
3 5
1 6
6 8
7 11

의 테스트 케이스를 작성하고 실제로 알고리즘의 구현도를 그려본 것이다.

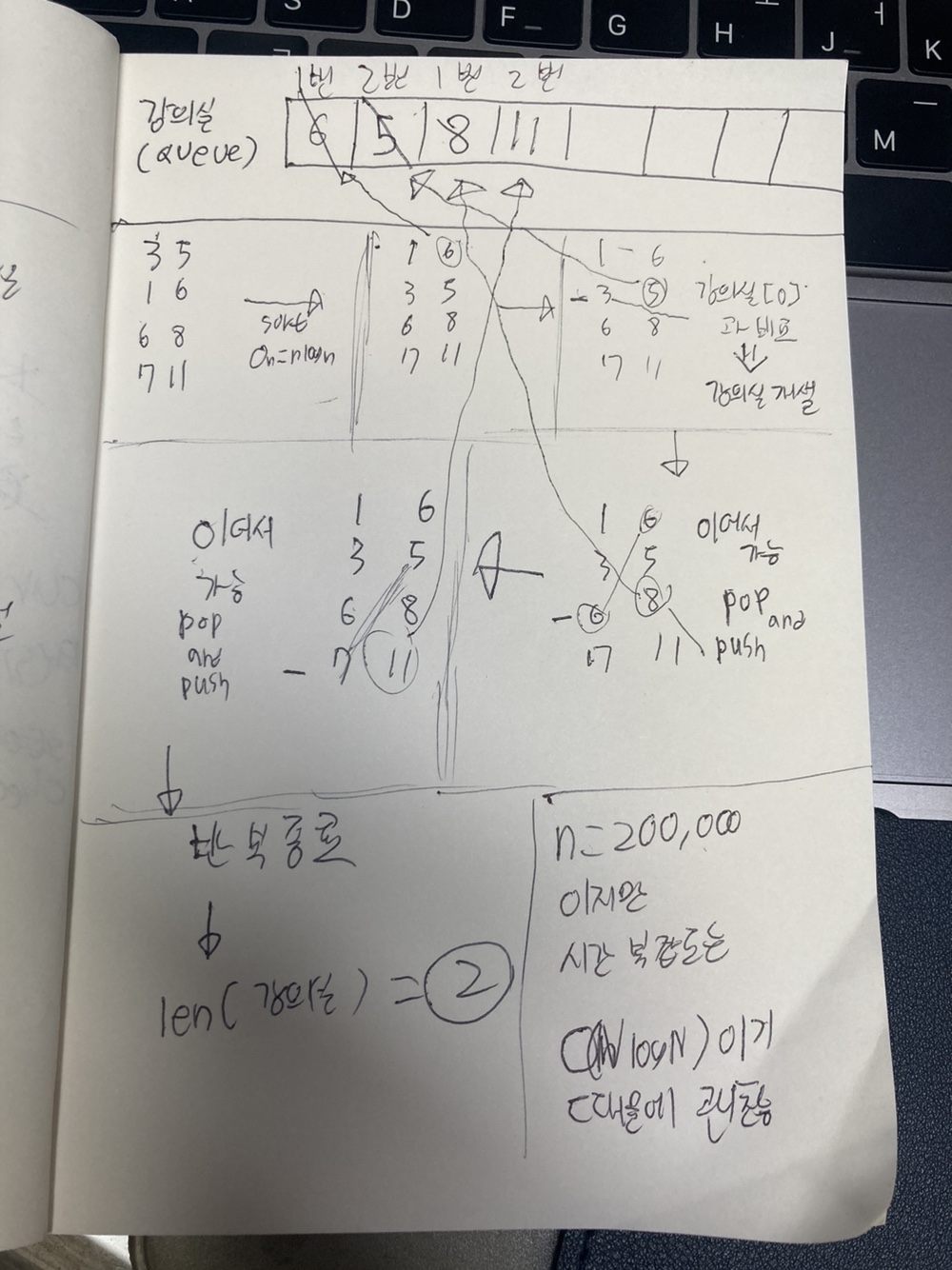
위 그림에서 오류는 heapq를 일반 큐로 인식하고 그렸다는 것이다.
heapq는 최소힙을 구현해주는 라이브러리로 항상 최소값을 pop()할 수 있다.

의문

왜 끝나는 시간 기준으로 정렬을 하면 안되는 것일까 ?

6
1 3
2 5
7 8
4 12
9 10
7 11
의 반례가 있다.

총평

우선 순위 큐로 수행시간을 줄이는 방법을 생각하지 못한다면 풀기 어려운 문제이다.
또한 그리디 기법을 이용할 줄 알아야한다.