
목차
1. 이진 트리
2. 느낀점
3. 참고자료
이진 트리
이진트리는 트리의 한 종류이다.
트리중에서도 각 노드의 자식 노드가 최대 2개인 경우를 '이진 트리'라고 한다.
트리 영역에서 가장 많이 사용되는 형태라고 한다.
이진 트리의 종류에는 편향 이진 트리, 포화 이진 트리, 완전 이진 트리가 존재한다.
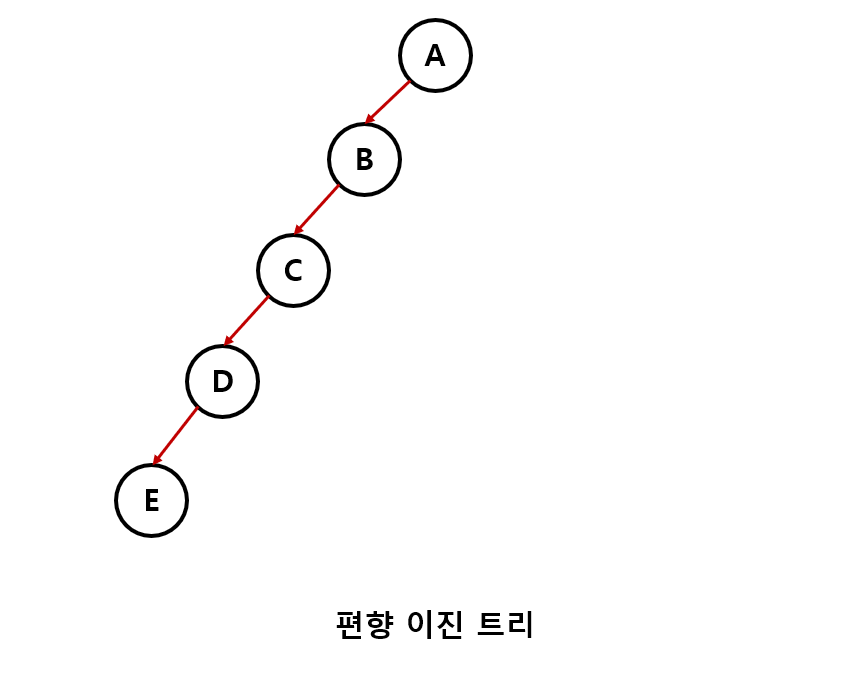
- 편향 이진 트리 : 노드가 한쪽 방향으로 편향된 이진 트리
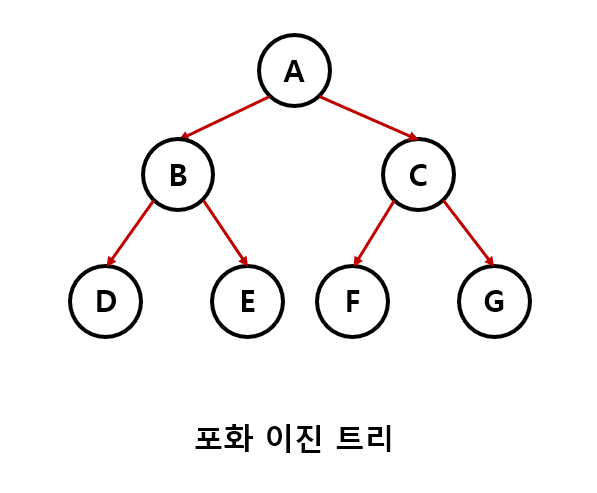
- 포화 이진 트리 : 트리의 높이가 모두 일정하며 리프 노드가 꽉찬 이진 트리
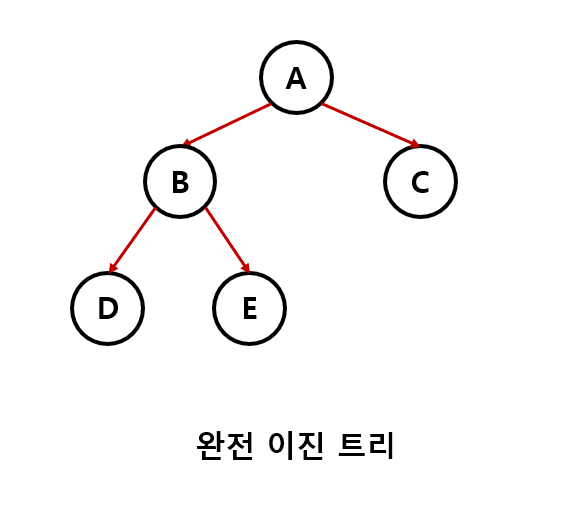
- 완전 이진 트리 : 마지막 레벨을 제외하고 완전하게 노드들이 채워져 있으며 마지막 레벨은 왼쪽부터 채워진 트리
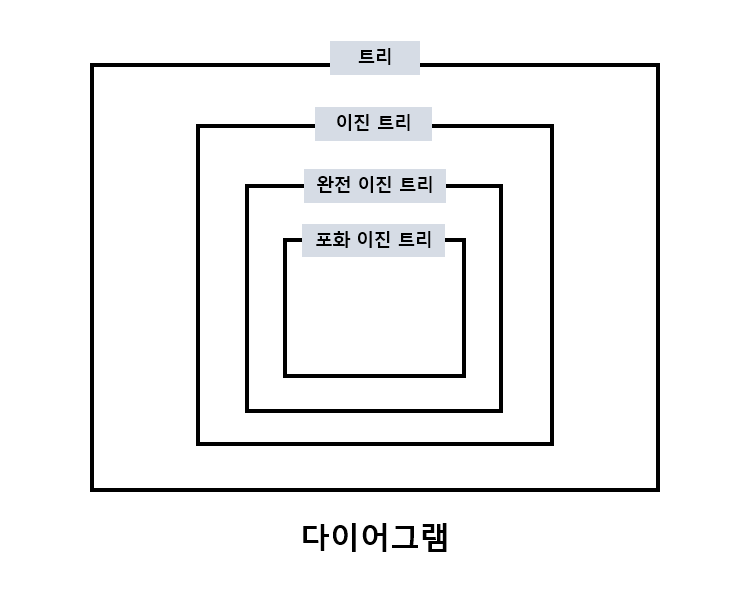
개념을 살펴보면 표화 이진 트리는 완전 이진 트리라고 볼 수 있다.
간단하게 포함 관계를 다이어그램으로 나타내면 다음과 같다.
보통 이진 트리는 문제에서 직접 사용되기 보다는 데이터를 저장할 때 사용되는 일종의 저장소 개념이라고 볼 수 있다.
이진 트리를 파이썬 기준으로 자료구조 형태로 나타내면 리스트로 나타내면 가장 직관적이다.
아래 그림과 같은 이진 트리가 존재한다면 인덱스가 1부터 시작하는 리스트에 옮기면 오른쪽 처럼 데이터가 저장된다.
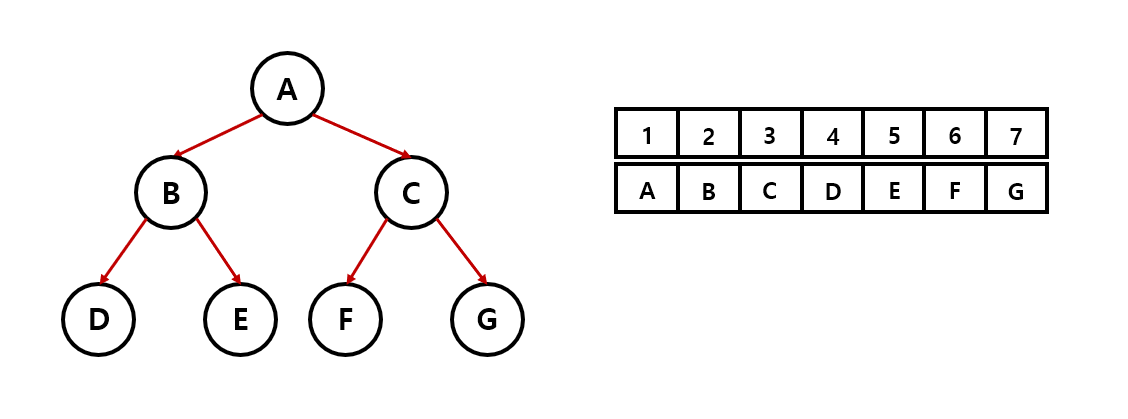
여기서 주의 할 점은 완전 이진 트리가 아닌 경우에도 노드의 인덱스는 바뀌지 않는다는 점이다.
아래 그림을 살펴보자.
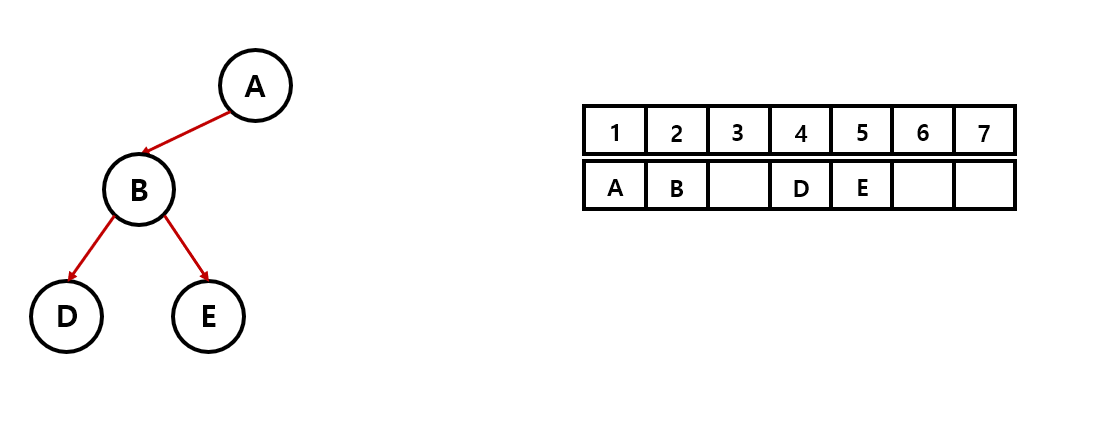
리스트의 빈 공간에는 NULL값을 채워준다고 생각하면 된다.
그렇다면 트리에서 노드끼리의 인덱스 관계는 어떻게 될까?
- 루트 노드로 이동할 경우 index = 1
- 왼쪽 자식 노드로 이동할 경우 index = index * 2
- 오른쪽 자식 노드로 이동할 경우 index = index * 2 + 1
- 부모 노드로 이동할 경우 index = index // 2
인덱스 연산 방식은 세그먼트 트리나 LCA 알고리즘에서 기본이 되는 연산이니 잘 숙지하자.
느낀점
트리라는 개념을 처음 접했을 때보다 글로 설명해보니 확실하게 이해하게 된것 같다.
아직 많은 문제를 풀었다고 할 수는 없지만 그간의 경험으로 트리는 그 자체로 물어보는 문제도 출제가 되지만 트리로 데이터를 어떻게 저장하느냐에 따라 공간 복잡도, 시간 복잡도가 차이가 나는 문제도 많다는 것을 느꼈다.
현재 하고있는 공부가 힘들 때 간혹 알고리즘 문제를 풀어보는데 이것마저 정체기가 온 것 같았다.
어쩌면 이제는 시간 복잡도가 아닌 공간 복잡도나 데이터 저장 방식에서 앞서나갈 실마리를 찾아야 할지도 모르겠다.
간단하고도 중요한 개념이지만 앞으로의 나에게 새로운 성장의 발판이 되는 장이었으면 좋겠다는 마음으로 이번 장을 마치도록 하겠다.
참고자료
DO IT 알고리즘 코딩 테스트 with 파이썬 - 김종관
코딩캠프 Tistory
서희찬님 Velog
오류가 존재하는 개념이 보인다면 알려주세요.