
목차
1. 세그먼트 트리
2. 느낀점
3. 참고자료
세그먼트 트리
세그먼트 트리는 자료구조의 일종으로 구간 합, 구간 최대, 구간 최소, 구간 곱 과 같은 문제를 빠르게 풀 수 있도록 해준다.
이름에서도 알 수 있듯이 트리의 한 종류이다.
세그먼트 트리는 완전이진 트리로 구현할 수 있다.
구현 단계는 다음과 같이 나눌 수 있다.
- 초반 트리 만들기(트리 초기화하기)
- 요구하는 값 구하기(질의값 구하기)
- 데이터 업데이트하기
위 과정을 통하여 세그먼트 트리를 만들고 데이터를 저장하고 접근할 수 있다.
세그먼트 트리의 가장 큰 장점은 데이터 업데이트를 빠른 속도로 할 수 있다는 것이다.
기존 구간 합(Prefix Sum) 알고리즘을 살펴보면 질의값에 대해서는 O(N)으로 높은 효율성을 보여줬으나, 만약 중간에 데이터가 바뀌는 경우에는 데이터가 바뀔때마다 최악의 경우 한번 더 O(N)의 시간복잡도를 사용해야할 수도 있다.
구간 합의 문제점을 그림을 통해서 간단하게 알아보자.

데이터를 이용하여 구간 합 리스트를 구현한 후 구간 합을 빠르게 구할 수 있다는 걸 우리는 알고있다.
하지만 데이터가 변경된다면 업데이트하는데 오래걸린다는 치명적인 단점이 있다.
하나의 데이터가 업데이트되면 그 뒤에있는 값들에 차이값만큼 더해줘야한다.
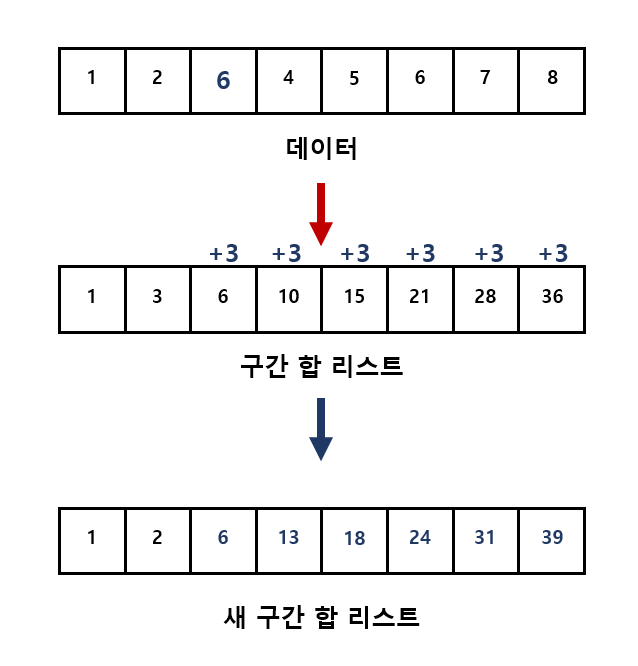
이런 문제점을 해결하고자 '세그먼트 트리'라는 자료구조가 만들어졌다.
세그먼트 트리는 이진 트리로 구현이 가능한데 말로 설명하는 것보다 그림으로 이해하는 것이 빠를 것이다.
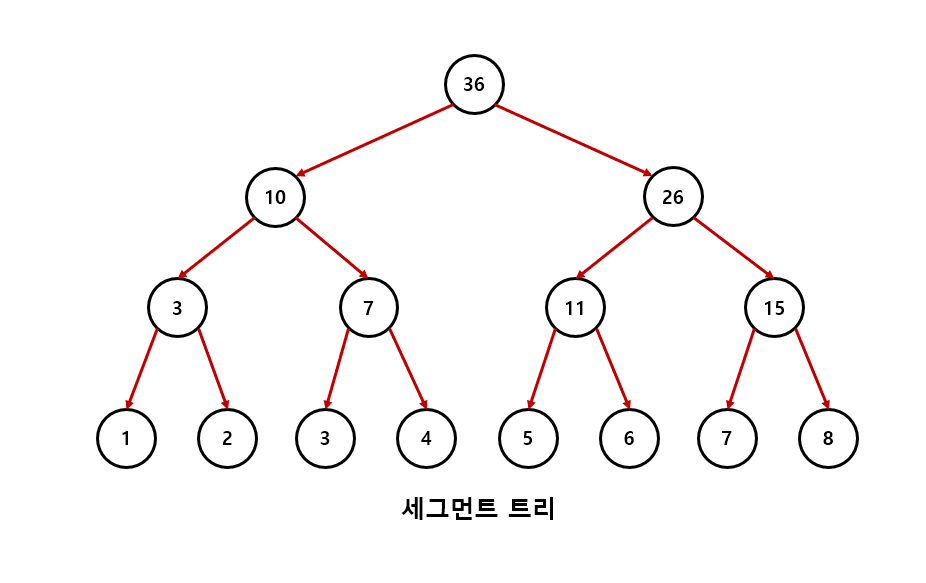
위 데이터를 구간 합 기준 세그먼트 트리로 구현하면 다음과 같다.
가장 마지막 레벨에 데이터를 차례로 나열한 뒤 각 부모 노드에 더해주면된다.
세그먼트 트리는 1차원 리스트로 구현하는데 그때 인덱스는 1부터가 아니라는점에 주의하도록 하자.
여기서는 개념 자체에만 집중할 것이니 코드에 관한 설명은 생략하도록 하겠다.
세그먼트 트리를 이용하여 구간 합을 어떻게 구할까?
만약 2 - 5번 인덱스의 구간 합을 구해야한다고 가정하면 다음 그림과 같이 구할 수 있다.
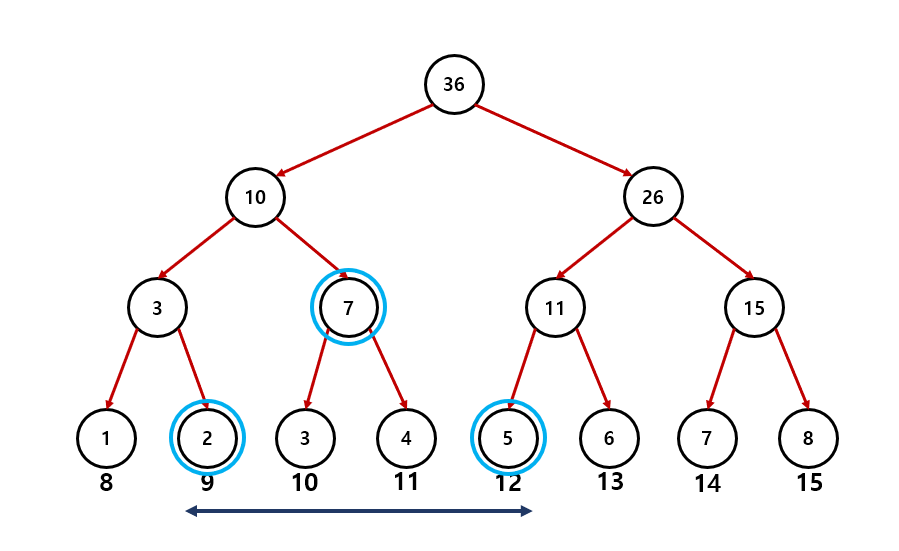
세그먼트 트리의 강점중 하나는 효율적으로 데이터를 수정할 수 있다는 점이었는데 그 부분에 대해서도 한번 살펴보자.
세그먼트 트리의 경우 각 노드에 영향을 미치는 노드는 자식노드이다.(리프노드 제외)
어떤 노드가 변경되었을 때 그 위에있는 부모노드를 타고 올라가 루트노드까지 변경해주면 된다.
3번 째 노드가 6으로 바뀌었다고 가정해보자.
그럼 다음과 같이 바뀌게 된다.
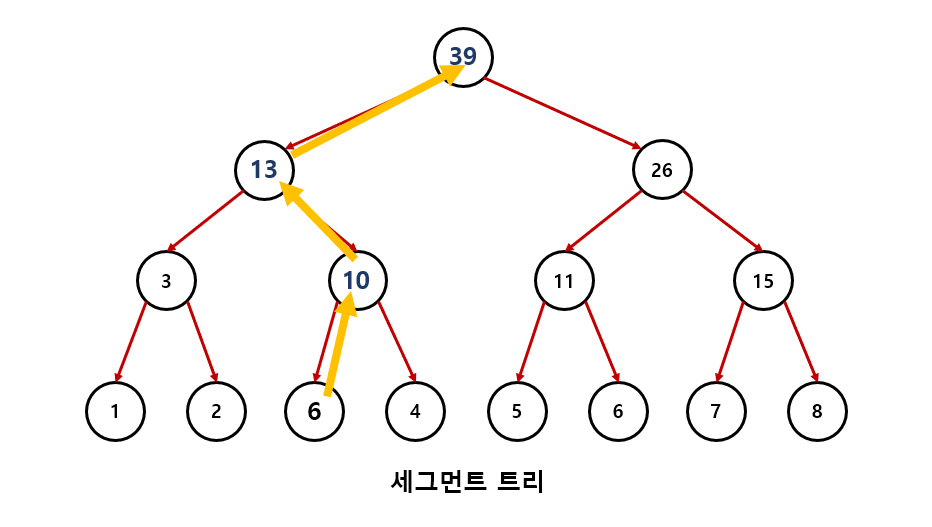
위 그림과 같이 각 노드의 부모노드로 올라가며 루트노드에 도달할 때까지 차이값만큼 더해주면 데이터의 수정이 끝난다.
위 예시는 작은 데이터를 보았기에 4개의 데이터를 고치는거나 6개의 데이터를 고치거나 별 차이가 없다고 느낄 수 있지만 데이터가 커질수록 극심한 차이가 난다.
느낀점
확실히 어렵다.
이진트리 자체는 어렵지 않으나 구현이 만만치 않다.
구현을 하려면 앞 장에서 설명한 인덱스간의 관계에 대해서 잘 알아야한다. 여기서 구현은 하지 않았지만 백준 관련 문제를 풀면서 실력을 쌓으면 좋을것 같다.
참고자료
DO IT 알고리즘 코딩테스트 with 파이썬 - 김종관