
목차
1. LCA
2. 느낀점
3. 참고자료
LCA
LCA라고도 불리는 최소 공통 조상은 트리의 두 노드가 자신을 포함하는 조상중 가장 가까운 공통 조상을 찾는 알고리즘이다.
예를 들어 아래와 같은 구조의 트리가 존재한다고 할 때
노드 5와 4의 LCA는 2이며
노드 5와 6의 LCA는 1이다.
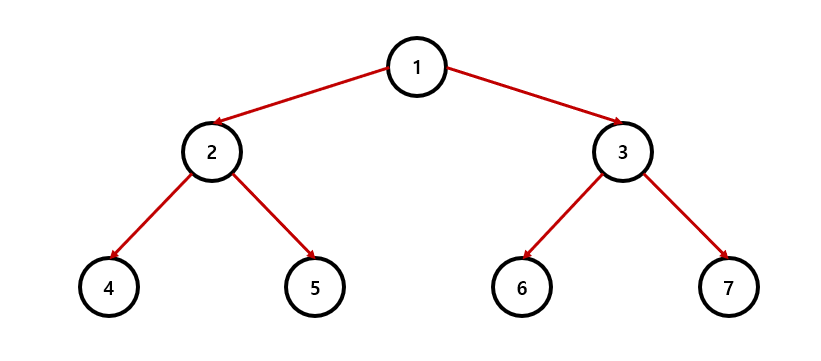
간단하게 그림으로 그려보면 다음과 같다.
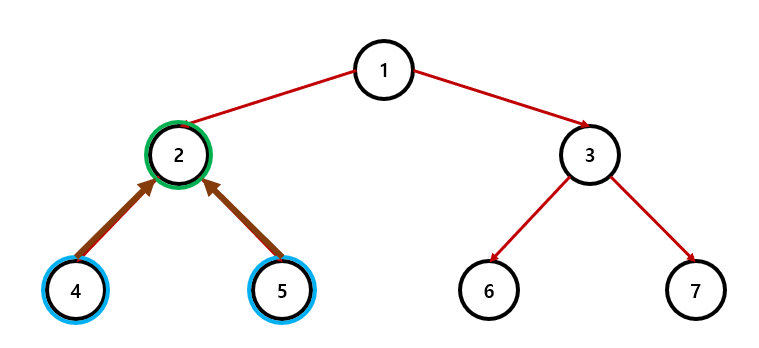
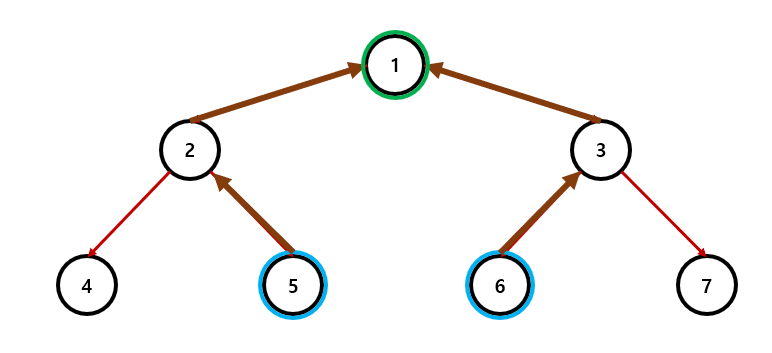
그렇다면 최소 공통 조상을 찾는 방법은 무엇일까?
알고리즘은 다음과 같다.
- 두 노드중 더 깊은 곳에 위치한 노드가 존재하는지 확인한다.
- 존재한다면 더 깊은 곳에 위치한 노드를 더 얕은 곳에 위치한 노드와 같은 레벨로 맞춰준다.
- 존재하지 않는다면 2번 과정을 뛰어넘는다
- 차례대로 각 노드의 조상 노드를 방문하며 같으면 종료후 출력한다.(이때 자기 자신도 자신의 조상임에 주의하자.)
문제 상황을 가정해보자.
- 어떤 트리 구조가 주어진다.
- 두 노드 a, b가 주어진다.
- LCA(a, b)를 구한다.
이제 차례대로 풀어보도록 하자.
- 어떤 트리 구조가 주어진다.
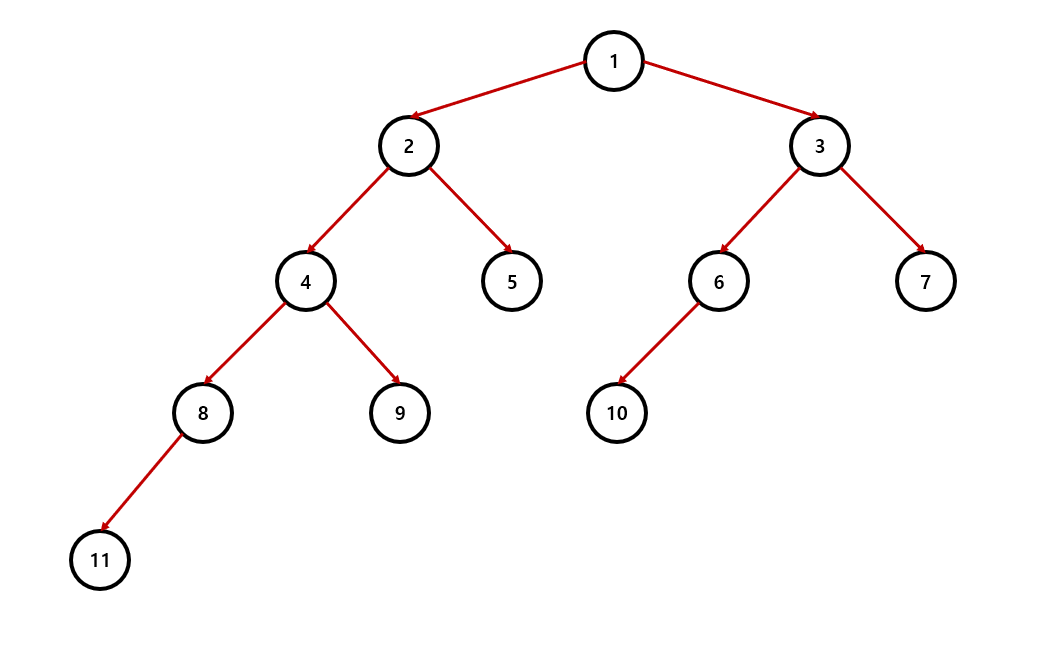
- 두 노드 a, b가 주어진다.
여기서는 a = 11, b = 5라고 가정하겠다.
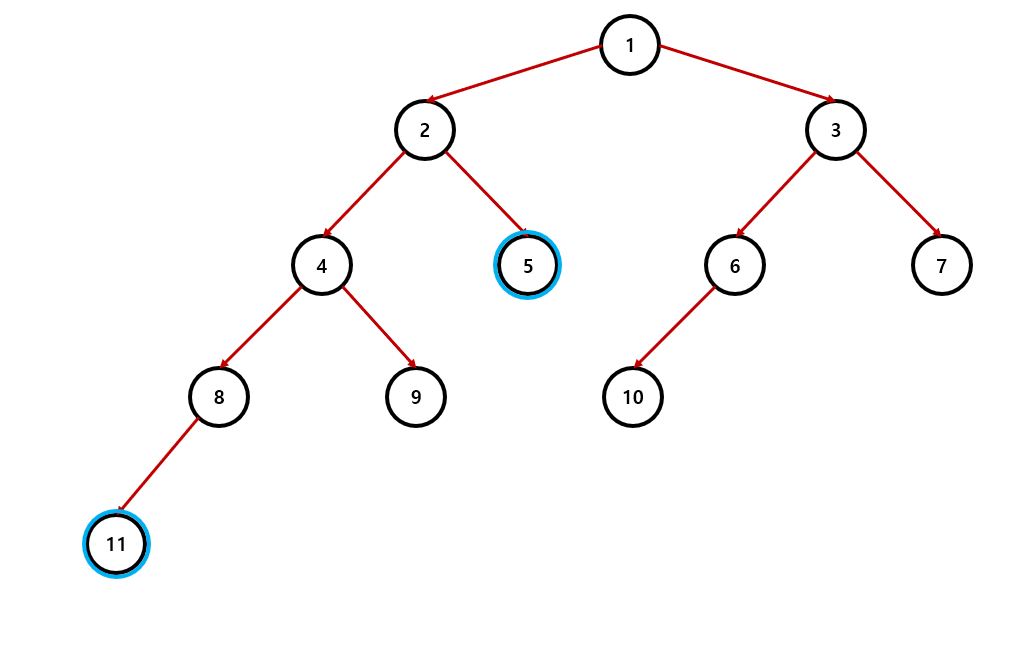
이제 앞에서 살펴본 LCA 알고리즘을 적용해보도록 하자.
(1). 현재 노드 11의 레벨(깊이)은 5이고, 노드 5의 레벨은 3이다.(루트 노드의 레벨을 1이라고 가정)
(2). 더 깊은 노드가 존재하므로 노드 11의 레벨을 노드 5의 레벨까지 맞춘다.(레벨이 더 작은 노드로 맞춘다.)
(3). 2번 과정을 시행하면 각 노드는 4, 5를 가르키게 된다.
(4). 조상 노드를 계속 확인해가며 같아질 때까지 반복한다.
그림을 통해서 과정을 살펴보자.
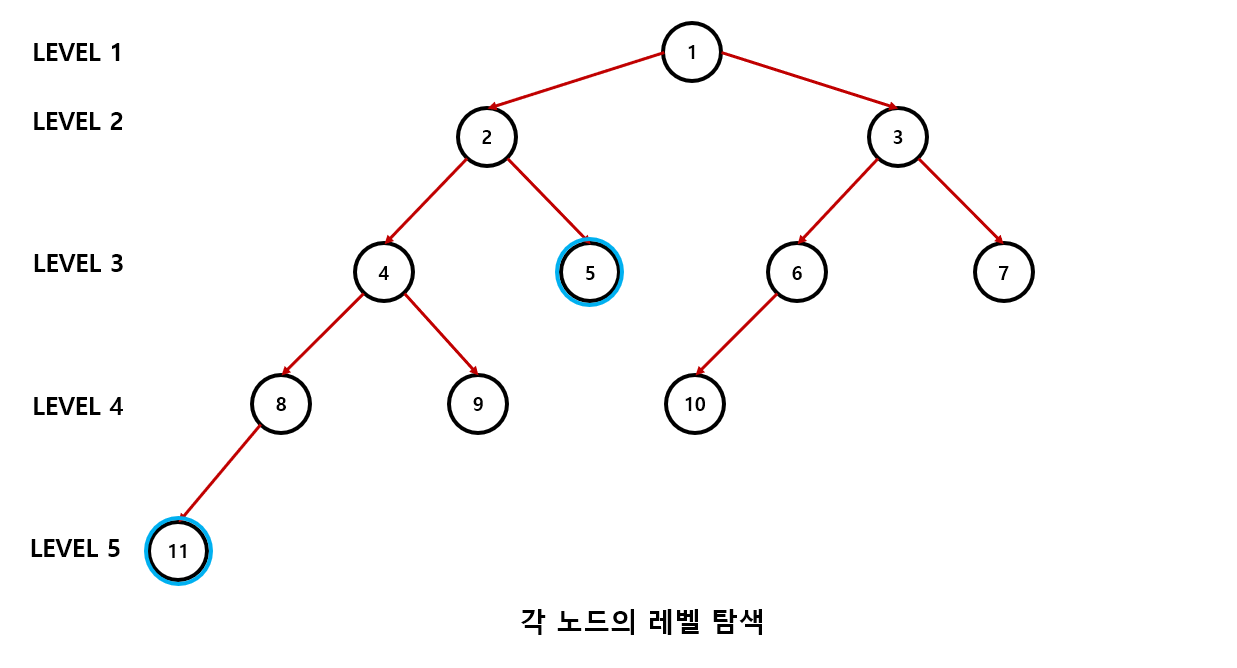
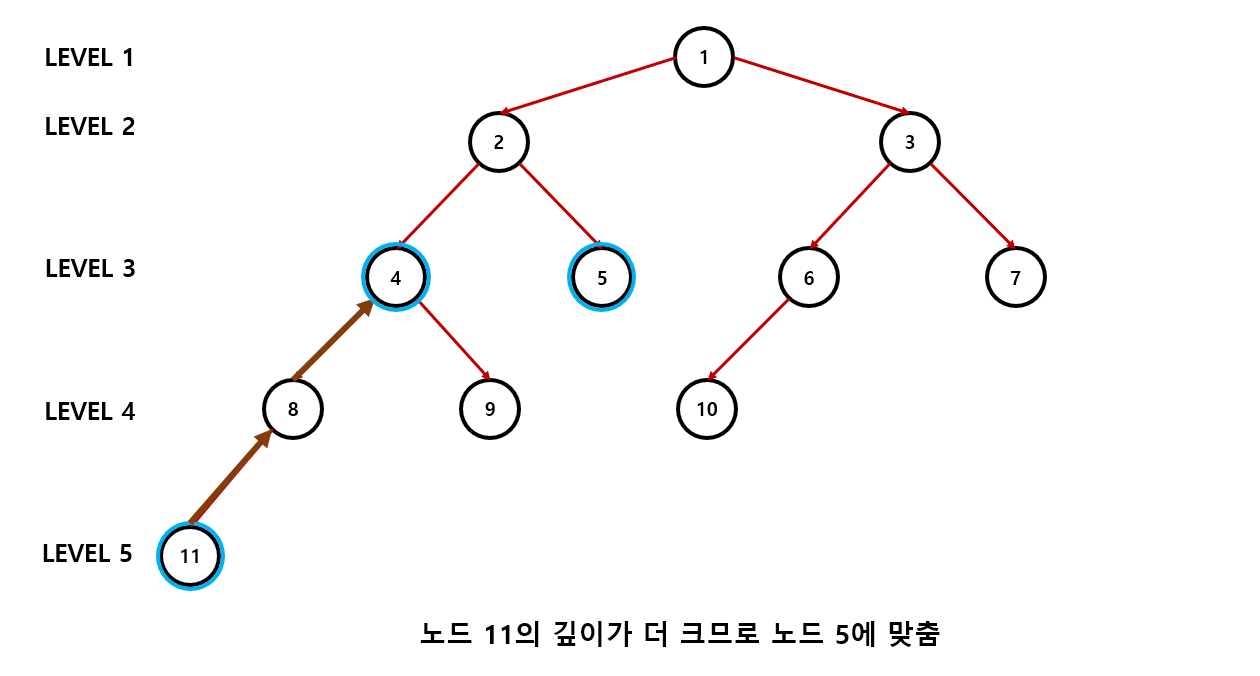
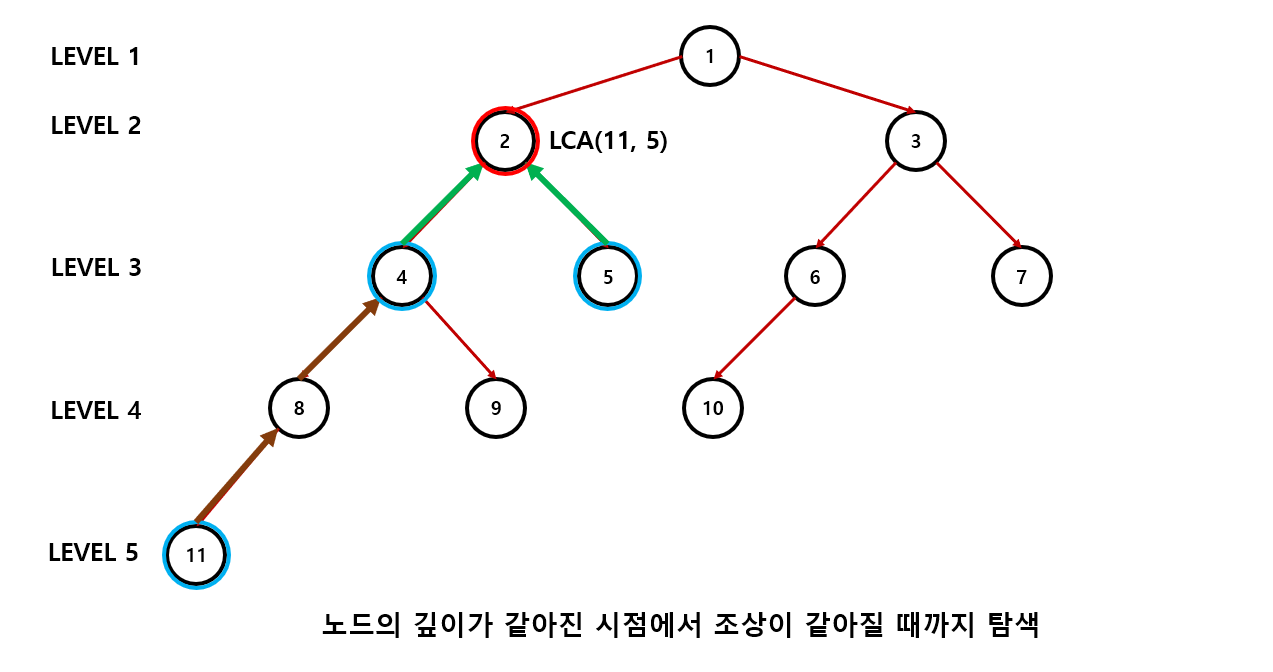
이론상으로는 그렇게 어렵지 않으나 코드로 구현해보면 좀 복잡해진다.
그리고 이렇게 구현한 알고리즘으로는 한계가 있어 더 빠른 알고리즘이 필요해지는데 그게 바로 '최소 공통 조상 빠르게 구하기'이다.
이 부분은 좀 어려워진다.
하지만 이번 장에서 습득한 기본 개념을 확실하게 하면 약간의 변형을 이용해 '최소 공통 조상 빠르게 구하기'를 쉽게 이해할 수 있으므로 확실하게 습득해두자.
느낀점
LCA를 공부하며 이론적으로는 쉬웠으나 구현할 때 애를 먹었던 것 같다.
이해하면 쉬운 코드, 이해하지 못하면 어려운..
더 확실하게 익히도록 하자
참고자료
DO IT 알고리즘 코딩테스트 with 파이썬 - 김종관