컴퓨터의 작동방식
컴퓨터는 2진수를 사용한다고 예전부터 많이 들었다.
처음에는 무슨 말인지 이해가 안됐었다.
컴퓨터도 전자기기이므로 전원의 on, off 두 상태를 활용하기 때문이다.
전구 하나를 가지고 불을 키고 끄는 행위에 의미를 부여하면 두 가지의 정보를 표현할 수 있다.
전구 3개가 있으면 2의 3제곱에 해당되는 총 8가지의 정보를 표현할 수 있는 것이다.
과거에는 정말 전구와 같은 역할을 하는 진공관으로 정보를 저장했고
현대에는 트랜지스터의 발명으로 눈으로도 보이지 않을 정도로 미세한 전자 소자들로
정보를 저장할 수 있도록 집적회로에 구현되어 있다.
결국 컴퓨터는 모든 작업을 0과 1의 조합인 2진수로 만들어서 처리한다.
문자의 표현
우리 인간의 언어를 컴퓨터가 처리할 수 있는 2진수로 바꾸기 위해서는
우선 문자들을 모두 숫자에 대응시켜야 한다. 이를 위해서 ASCII 코드를 사용한다.
ASCII 코드는 7bit로 총 128가지의 부호가 사용된다.
ASCII 코드는 영문 알파벳에 한정적이라서, 우리나라의 한글과 같이
전 세계 모든 문자와 언어를 대응시키기 위해서
아스키 코드보다 확장된 유니코드라는 산업표준이 설계되었다.
유니코드가 널리 쓰이고 있더라도 직접 활용해본 적은 거의 없는 것 같다.
사용 환경에 따라서 한글을 입력하려고 할 때, 문제가 생기는 경우가 꽤 있는데
불편한 상황을 마주하게되면 유니코드에 대해 좀 더 자세히 공부해봐야 겠다.
아래 표에 문자열을 다룰 때 주로 사용되는 ASCII 코드를 정리해 놓았다.
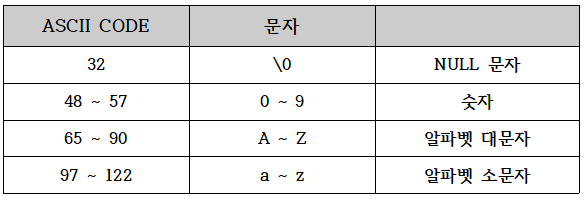
- 자료형이
char일 때, 그 값을 ASCII code로 해석한다. - 홑따옴표
' '로 묶어주면 해당 문자의 ASCII code로 해석하며, 가독성이 좋아짐.
정수의 표현
정수의 표현범위
정보의 최소단위를 bit (binary digit) 라고 한다.
전구 하나 또는 트랜지스터 하나가 1bit 인 것이다.
그리고 8bit 를 1byte라고 한다.
컴퓨터도 만능이 아니고 용량의 한계가 있기 때문에, 항상 자료형의 크기를 염두에 두고
코드를 짜야된다.
아래에 기억해둘만한 단위들의 정수 표현범위를 정리해보았다.
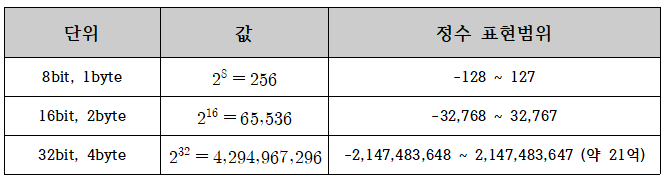C의 자료형 중에서 char는 1byte이고, int는 4byte이다. int의 표현 범위가 꽤 넓다고 볼 수 있어서 일반적인 연산으로는 벗어날 일이 잘 없지만, 수치 해석과 같이 큰 값으로 넘어갈 수 있는 연산에 대해서는 이 정수 표현범위에 대해서 잘 생각하고 코드를 짜야 된다.
MCU 같은 환경에서는 int 자료형이 꼭 4byte라는 보장이 없다.
환경에 따라 코드를 짜기전에 사용하고자 하는 자료형의 크기를 정확히 확인하는 것은 필수다.
혹시나 표현 범위를 넘어갈 경우 해결할 수 있는 3가지 방법이 있다.
- 비트를 늘린다.
- 부호를 사용하지 않는다.
- 단위를 바꾼다.
비트를 하나씩 늘릴 때마다 표현범위는 두 배씩 늘어난다. 사용하는 정수의 한계가 정해져 있다면 그 크기에 맞게 메모리를 사용하는 것이 가장 효율적이지만, 더 큰 자료형으로 바꾸는 것이 일반적이다.
사용환경에 따라 다르지만 일반적으로 부호를 사용하는 것이 default이다. unsigned 자료형을 사용하면 부호 비트를 활용할 수 있기 때문에, 한 비트를 늘린 것과 같은 효과를 누릴 수 있다.
음수를 사용하지 않음에도 표현범위를 벗어난다면 unsigned부터 고려해보자.
단위를 바꾸는 방법은 일종의 꼼수인데, 아주 큰 숫자들을 다룰 때 로그를 취하는 것과 같은 방식이다. 이 방법을 사용할 경우는 잘 없을 것 같다.
음수를 표현하는 방법
정수를 표현하는 것은 단순히 10진수를 2진수로 변환하면 되는데, 음수를 표현하는 것에 대한 고민이 필요하다. 내가 고민할 것은 아니고 이미 훌륭한 사람들이 해놓았다.
간단한 3bit 체계를 예시로, 음수 표현 방식을 살펴보자.
-
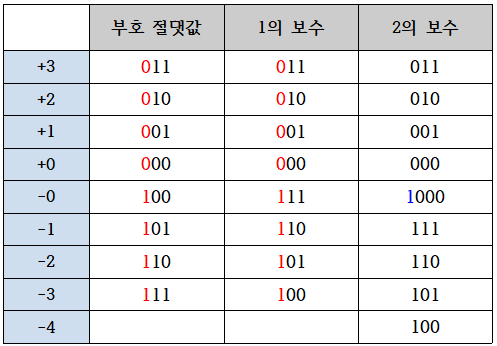
부호 절댓값 : 가장 직관적인 방식으로, 비트 하나를 더 사용해서 최상위 비트를 부호 비트로 사용한다.
-
1의 보수 : 양수에 대한 1의 보수를 음수로 사용한다. 1의 보수는 주어진 수와 더했을 때, 각 자릿수가 모두 1이 되도록 보조해주는 수이다.
-
2의 보수 : 양수에 대한 2의 보수를 음수로 사용한다. 주어진 이진수보다 한 자리 높고 가장 높은 자리가 1이며 나머지가 0인 수에서 주어진 수를 빼서 얻은 수가 2의 보수다. 또는 1의 보수에 1을 더해주면 쉽게 구할 수 있다.
2의 보수를 활용하면 두 가지 장점이 있다.
- 뺄셈 연산
- 숫자 한 개 더 표현
컴퓨터는 내부적으로 뺄셈 연산을 할 수 없다고 한다. 그래서 2의 보수를 활용해서 뺄셈을 한다.
뺄셈은 양수와 2의 보수로 표현된 음수의 덧셈으로 계산한다.
2의 보수에서 '-0'을 표현한 것을 보면 3bit를 초과한 것을 볼 수 있다. 파랗게 표시된 3bit를 초과한 1은 자리 올림수라고 한다. 체계를 벗어났으므로 자리 올림수는 무시된다. 결국 음수 0과 양수 0이 같은 방식으로 표현된다. 우리가 생각하는 수체계와도 일치하고 부호 절댓값이나 1의 보수 방식보다 숫자 하나를 더 표현할 수 있다는 장점이 있다.
대부분의 컴퓨터 체계가 2의 보수 방식을 사용한다고 한다. '대부분'이라고 방어적으로 말하는 것을 보면 예외는 있는 듯 하지만, 내가 그 예외를 만날 상황은 없을 것 같다..
