https://www.acmicpc.net/problem/2042
문제
어떤 N개의 수가 주어져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려 한다. 만약에 1,2,3,4,5 라는 수가 있고, 3번째 수를 6으로 바꾸고 2번째부터 5번째까지 합을 구하라고 한다면 17을 출력하면 되는 것이다. 그리고 그 상태에서 다섯 번째 수를 2로 바꾸고 3번째부터 5번째까지 합을 구하라고 한다면 12가 될 것이다.
입력
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄까지 N개의 수가 주어진다. 그리고 N+2번째 줄부터 N+M+K+1번째 줄까지 세 개의 정수 a, b, c가 주어지는데, a가 1인 경우 b(1 ≤ b ≤ N)번째 수를 c로 바꾸고 a가 2인 경우에는 b(1 ≤ b ≤ N)번째 수부터 c(b ≤ c ≤ N)번째 수까지의 합을 구하여 출력하면 된다.
입력으로 주어지는 모든 수는 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.
출력
첫째 줄부터 K줄에 걸쳐 구한 구간의 합을 출력한다. 단, 정답은 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.
접근
이 문제는 세그먼트 트리를 이용해 해결하는 문제이다.
세그먼트 트리
세그먼트 트리는 여러 개의 데이터가 연속으로 존재할 때 특정한 범위의 데이터의 합을 구할 때 사용하는 자료구조다. 배열에 들어있는 각 원소는 세그먼트 트리의 리프 노드를 구성하고 있으며 중간 노드는 자식 노드들의 합으로 이루어져 있으며 루트 노드는 배열에 들어있는 모든 노드의 합으로 구성되어 있다.
문제에서 제시된 입력은 다음과 같다.
| 1 | 2 | 3 | 4 | 5 |
이제 이 배열을 가지고 세그먼트 트리로 나타내면 다음과 같다.
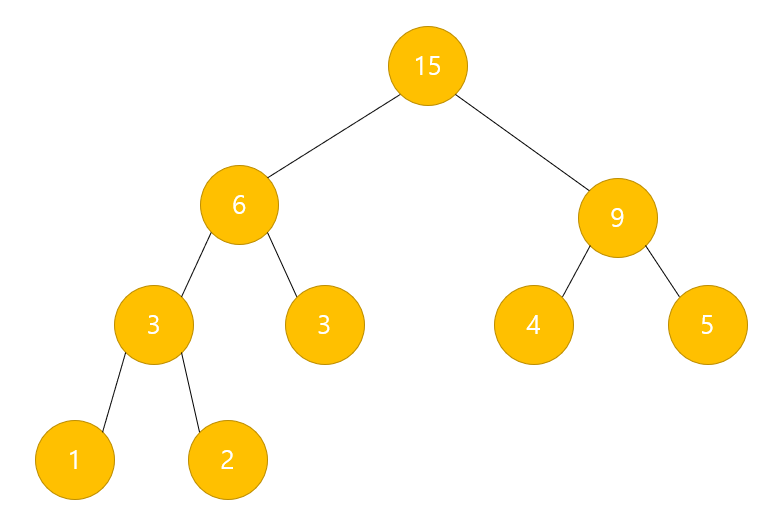
위에서 정리한 것처럼 본인의 값은 본인의 왼쪽 자식과 오른쪽 자식의 값을 더한 값으로 이루어져 있다.
본인은 보통 트리를 구성할 때 노드 구조체를 만들어서 구현하는 편인데, 이 문제같은 경우는 완전 이진 트리 형태로 왼쪽부터 꽉꽉 채워나가는 형태로 구성되기 때문에 좀 더 간단하게 배열로 구현하는 것이 좋을 것 같다.
세그먼트 트리를 구성하는 코드는 다음과 같다.
long long init(int low, int high, int idx) {
// 범위 시작점과 끝점이 같아지면
// 해당 인덱스(low or high)의 값을 트리 리프 노드 위치에 저장
if (low == high) {
tree[idx] = arr[low];
return tree[idx];
}
// 범위의 중간 지점을 기준으로
int mid = (low + high) / 2;
// 왼쪽 구간과 오른쪽 구간에 대해 재귀호출
// idx는 트리 상 인덱스를 의미하며
// 왼쪽 자식은 idx * 2, 오른쪽 자식은 idx * 2 + 1이 된다.
tree[idx] = init(low, mid, idx * 2) + init(mid + 1, high, idx * 2 + 1);
return tree[idx];
}전체적으로 봤을 때, 본인 기준으로 정해진 구간을 반으로 쪼갰을 때 왼쪽 구간에 대한 구간 합은 왼쪽 자식에, 오른쪽 구간에 대한 구간 합은 오른쪽 자식에 두게 된다. 또한, 구간 시작 점(low)과 구간 끝 점(high)이 같아지면 그 구간의 원소는 1개가 되고, 이는 리프 노드임을 뜻한다.
해당 위치에 값이 정해지면 그 값을 반환하고 반환된 값들을 더하면서 올라가는 방식이다.
tree[idx] = init(low, mid, idx * 2) + init(mid + 1, high, idx * 2 + 1);본인의 왼쪽과 오른쪽에 대해서 재귀호출하여 각각 반환된 값을 더한 값이 본인 위치의 값이 되는 것이다.
이렇게 트리를 완성시키고 나면 이제 문제를 해결해야 한다. 해결해야 하는 문제의 경우는 이렇게 두 가지가 있다.
- 특정 번호의 노드에 있는 값 변경
- 구간 b ~ c 까지의 값의 합 (b, c는 노드 번호)
1. 특정 번호의 노드에 있는 값 변경
a의 값으로 1을 입력했을 때 수행해야 하는 작업이다. 우선 코드는 다음과 같다.
void change(int b, int c, int low, int high, int idx, long long diff) {
if (b < low || b > high) {
return;
}
tree[idx] += diff;
if (low != high) {
int mid = (low + high) / 2;
change(b, c, low, mid, idx * 2, diff);
change(b, c, mid + 1, high, idx * 2 + 1, diff);
}
}b : 값을 바꿀 노드 번호
c : 바뀔 값 (다시 생각해보니 이 코드에서는 필요없을 듯 하다)
low : 구간의 시작
high : 구간의 끝
diff : 새로 바뀔 값과 기존 노드에 있던 값의 차이
구간 내에 값을 바꿀 번호(b)가 해당된다면, 그 노드에 들어있는 기존 값에 diff를 더해주는 작업을 해당 노드 번호가 있는 리프 노드에 도달할 때까지 반복한다.
어차피 특정 노드(리프노드 제외)를 기준으로 b가 속하는 구간을 가진 노드는 본인 + (왼쪽 자식 or 오른쪽 자식)이 된다. 따라서 이러한 방식으로 내려가면 나중에 본인 노드의 자식들을 더한 값이 본인의 값이 된다.
방법 2
위의 방식은 개인적으로 찾아봤을 때 대부분 저 방식으로 구현되었고, 본인은 처음에 이렇게도 코드를 짜보았다.
long long change(int b, long long c, int low, int high, int idx) { if (b < low || b > high) { return tree[idx]; } if (low == high && b == high) { tree[idx] = c; return tree[idx]; } if (low <= b && b <= high) { int mid = (low + high) / 2; tree[idx] = change(b, c, low, mid, idx * 2) + change(b, c, mid + 1, high, idx * 2 + 1); } return tree[idx]; }위의 방식과 비슷하지만, 일단 리프 노드까지 탐색한 후, 해당 리프 노드에 도달하면 그 노드의 값와 반대쪽 자식의 값을 더한 값으로 부모 노드 값을 갱신하고 이 작업을 반복하는 쪽으로 구성을 해보았다.
(처음에 트리를 구성할 때와 비슷한 방식)
2. 구간 b ~ c 까지의 값의 합 (b, c는 노드 번호)
코드는 다음과 같다.
long long get(int b, int c, int low, int high, int idx) {
// 구하고자 하는 구간이 현재 범위를 아예 벗어난 경우
if (b > high || c < low) {
return 0;
}
// 구하고자 하는 구간 내에 현재 범위가 모두 포함된 경우
if (b <= low && high <= c) {
return tree[idx];
}
// 구하고자 하는 구간에 현재 범위가 걸쳐있는 경우
int mid = (low + high) / 2;
return get(b, c, low, mid, idx * 2) + get(b, c, mid + 1, high, idx * 2 + 1);
}b : 구하고자 하는 구간의 시작
c : 구하고자 하는 구간의 끝
low : 현재 구간의 시작
high : 현재 구간의 끝
idx : 트리 상 현재 인덱스
다음과 같은 트리가 있다고 가정하고, a=3, b=9일 때의 답을 구해볼 예정이다.
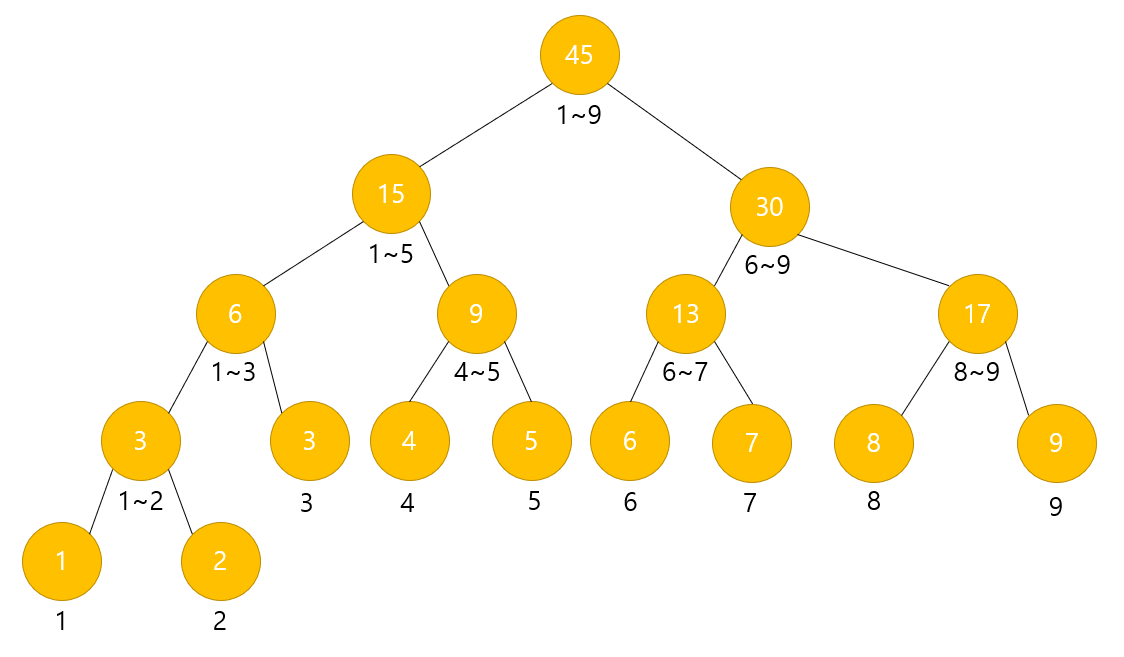
원 안의 숫자는 노드가 가진 값 (범위에 속한 노드의 값의 합), 밑의 숫자는 노드 번호 (범위)를 의미한다.
먼저 루트부터 탐색한다.
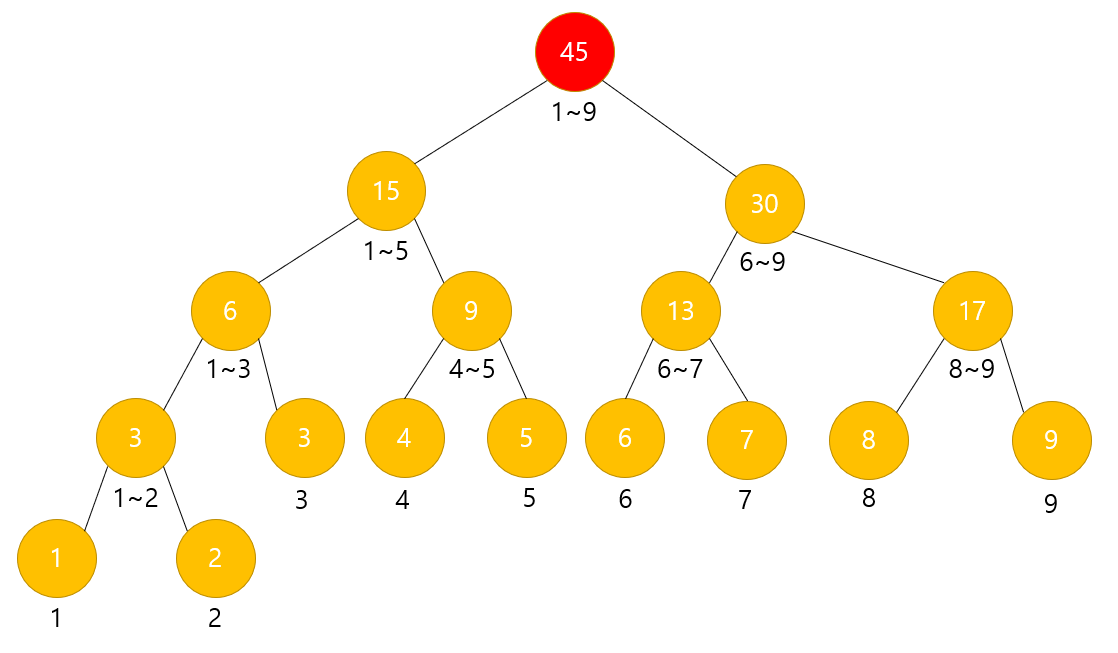
a = 3
b = 9
low = 1
high = 9
구하고자 하는 범위 : 3 ~ 9
현재 범위 : 1 ~ 9
현재 범위가 구하고자 하는 범위에 걸쳐져 있는 상태이므로 자식 노드들을 탐색한다.
(구하고자 하는 범위를 현재 범위가 감싸는 형태도 걸쳐져있는 것으로 본다.)
먼저, 왼쪽 자식부터 탐색한다.
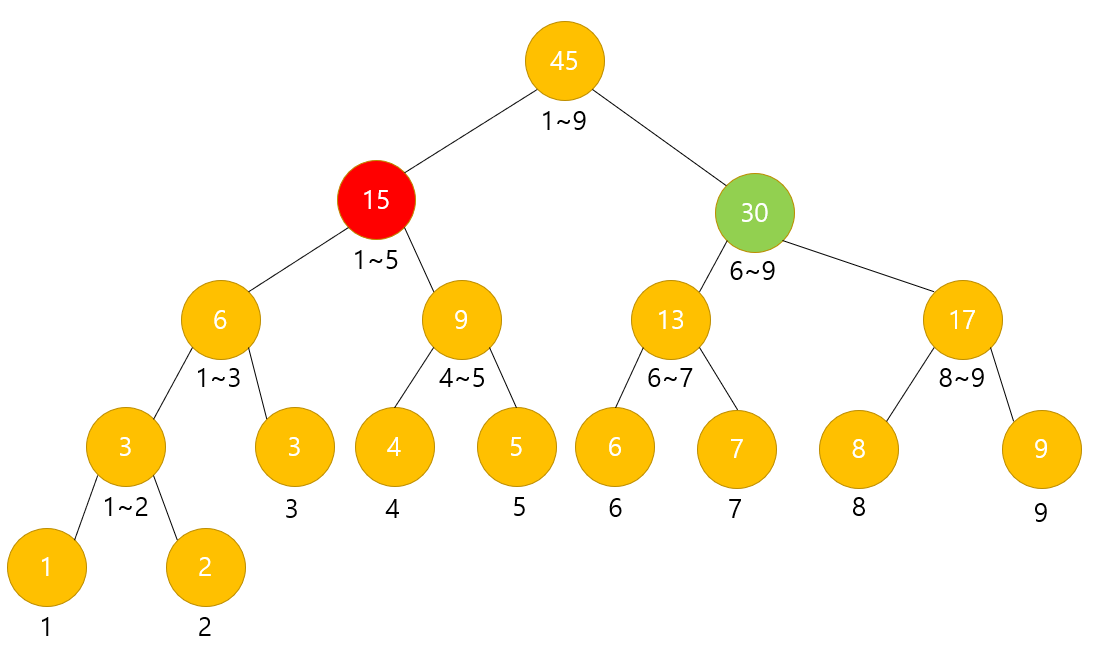
(빨간색은 현재 노드, 초록색은 나중에 탐색할 노드다.)
a = 3
b = 9
low = 1
high = 5
구하고자 하는 범위 : 3 ~ 9
현재 범위 : 1 ~ 5
현재 범위가 구하고자 하는 범위에 걸쳐져 있는 상태이므로 자식 노드들을 탐색한다.
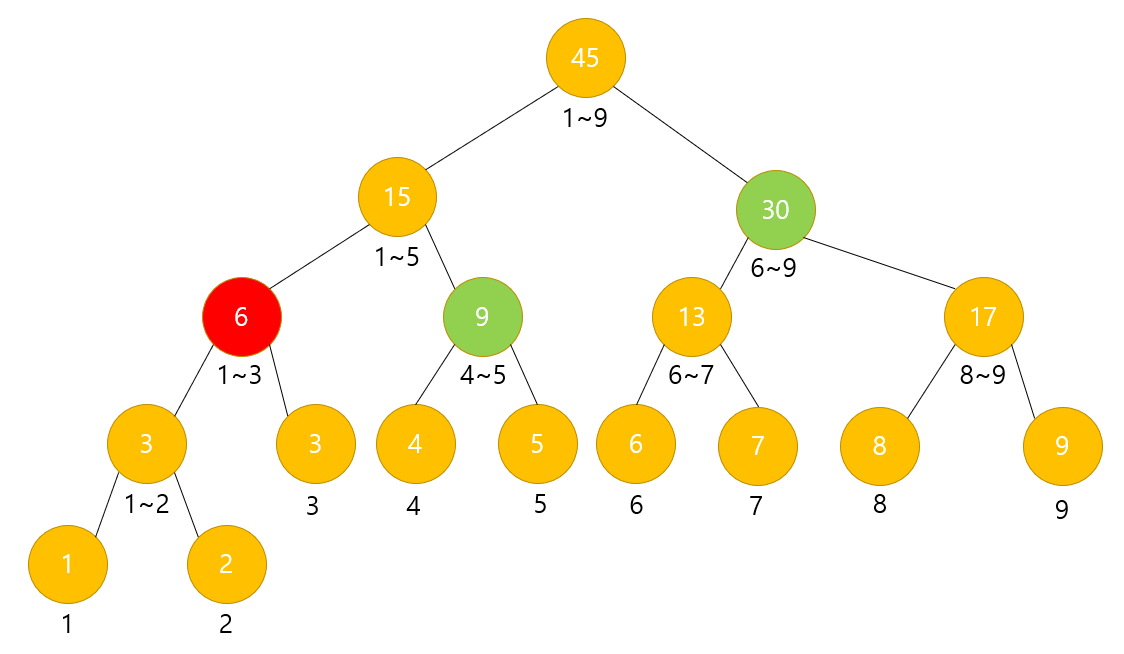
(빨간색은 현재 노드, 초록색은 나중에 탐색할 노드다.)
a = 3
b = 9
low = 1
high = 3
구하고자 하는 범위 : 3 ~ 9
현재 범위 : 1 ~ 3
현재 범위가 구하고자 하는 범위에 걸쳐져 있는 상태이므로 자식 노드들을 탐색한다.
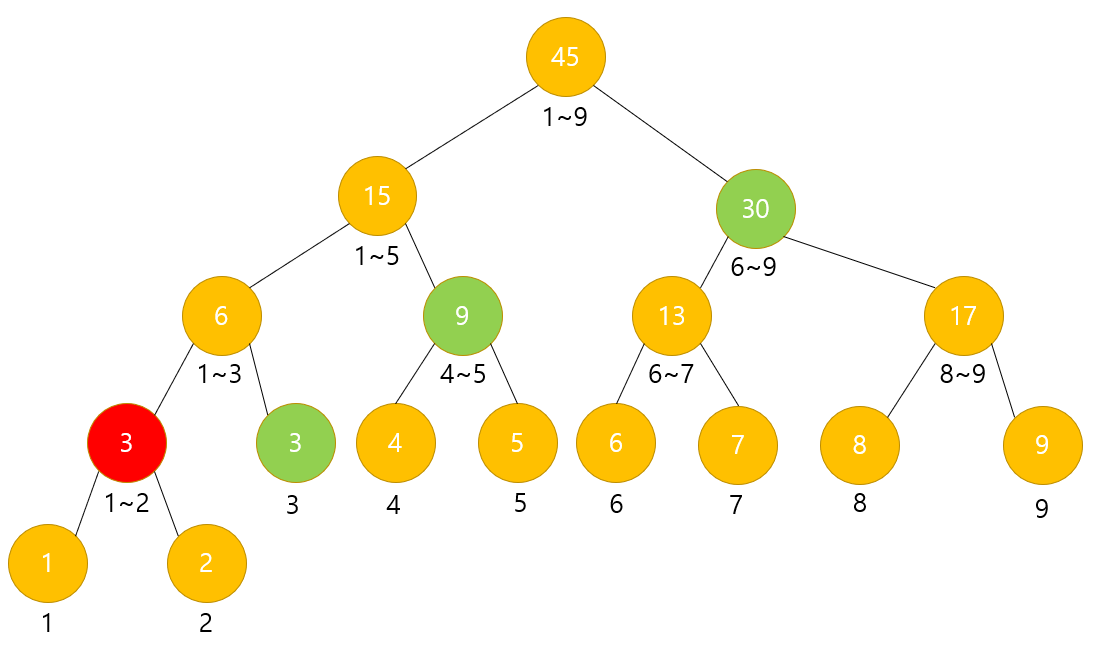
(빨간색은 현재 노드, 초록색은 나중에 탐색할 노드다.)
a = 3
b = 9
low = 1
high = 2
구하고자 하는 범위 : 3 ~ 9
현재 범위 : 1 ~ 2
현재 범위가 구하고자 하는 범위를 완전히 벗어나므로 빠져나온다.
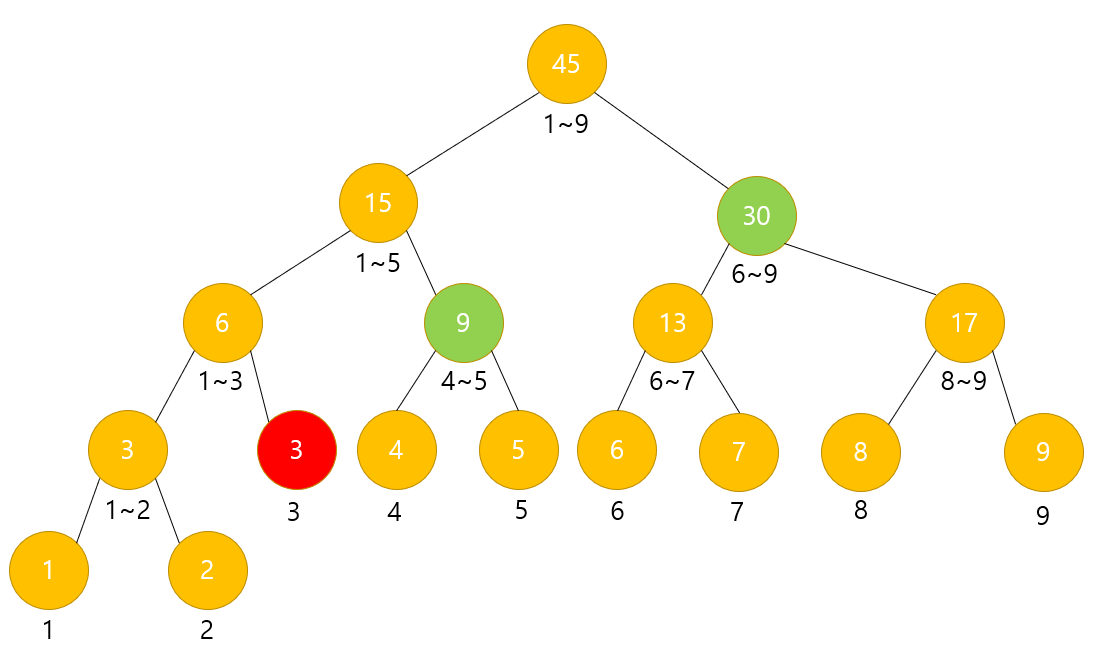
(빨간색은 현재 노드, 초록색은 나중에 탐색할 노드다.)
a = 3
b = 9
low = 3
high = 3
구하고자 하는 범위 : 3 ~ 9
현재 범위 : 3
현재 범위가 구하고자 하는 범위에 속한다. 따라서 해당 노드의 값은 정답에 합해지게 된다.
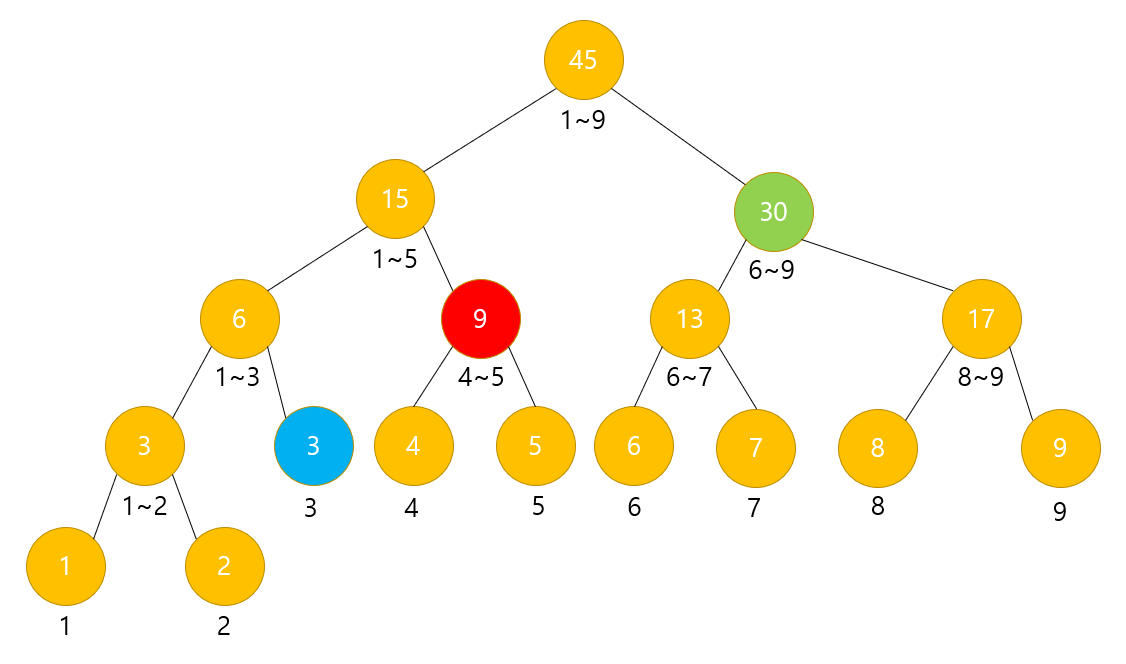
(빨간색은 현재 노드, 초록색은 나중에 탐색할 노드이며 하늘색은 확정된 노드다.)
a = 3
b = 9
low = 4
high = 5
구하고자 하는 범위 : 3 ~ 9
현재 범위 : 4 ~ 5
현재 범위가 구하고자 하는 범위에 속한다. 따라서 해당 노드의 값은 정답에 합해지게 된다.
(빨간색은 현재 노드, 초록색은 나중에 탐색할 노드이며 하늘색은 확정된 노드다.)
a = 3
b = 9
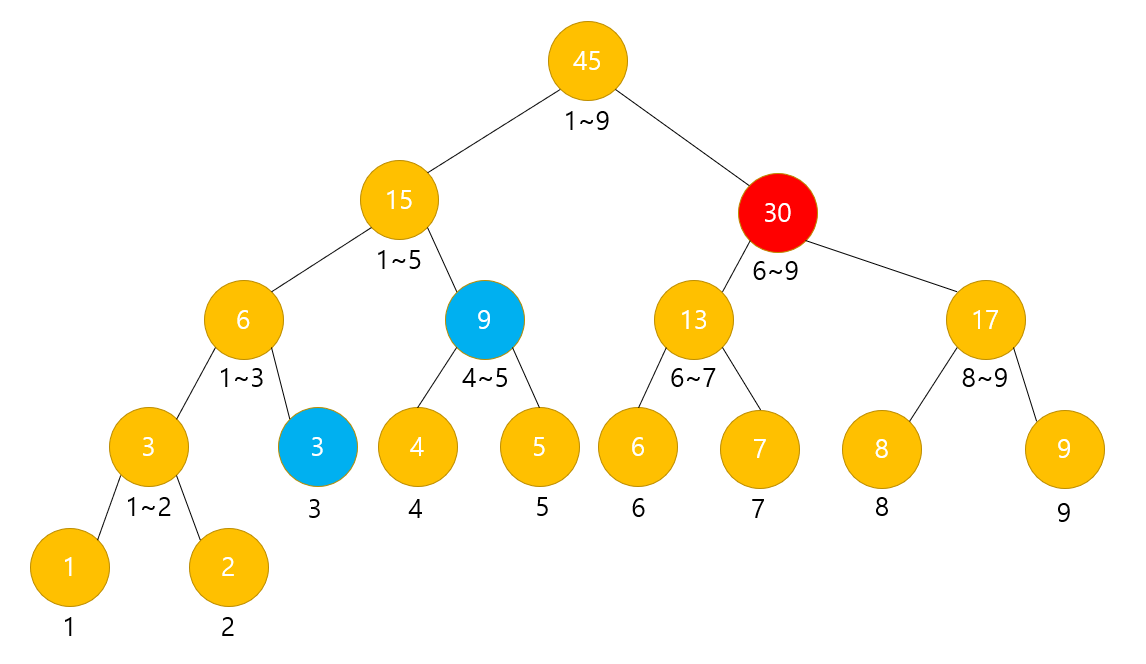
low = 6
high = 9
구하고자 하는 범위 : 3 ~ 9
현재 범위 : 6 ~ 9
현재 범위가 구하고자 하는 범위에 속한다. 따라서 해당 노드의 값은 정답에 합해지게 된다.
정답
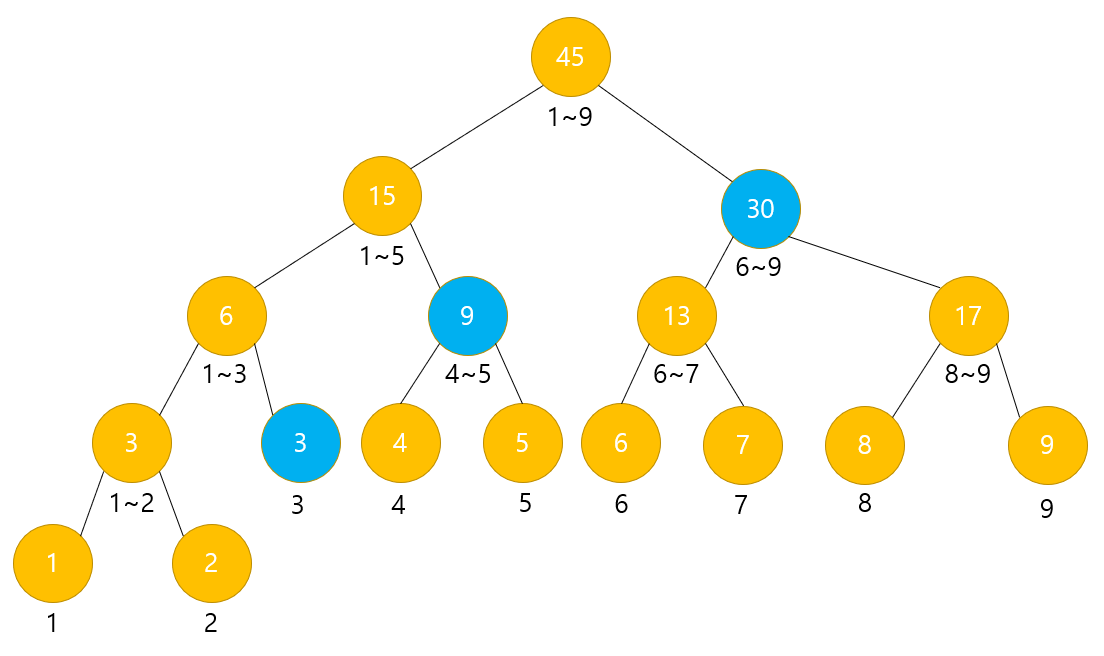
3 + 9 + 30 = 42
코드
#include <iostream>
using namespace std;
const int max_num = 1e6 + 1;
long long arr[1000001];
long long tree[4000004];
int n;
int m;
int k;
long long init(int low, int high, int idx) {
if (low == high) {
tree[idx] = arr[low];
return tree[idx];
}
int mid = (low + high) / 2;
tree[idx] = init(low, mid, idx * 2) + init(mid + 1, high, idx * 2 + 1);
return tree[idx];
}
void change(int b, int c, int low, int high, int idx, long long diff) {
if (b < low || b > high) {
return;
}
tree[idx] += diff;
if (low != high) {
int mid = (low + high) / 2;
change(b, c, low, mid, idx * 2, diff);
change(b, c, mid + 1, high, idx * 2 + 1, diff);
}
}
long long get(int b, int c, int low, int high, int idx) {
if (b > high || c < low) {
return 0;
}
if (b <= low && high <= c) {
return tree[idx];
}
int mid = (low + high) / 2;
return get(b, c, low, mid, idx * 2) + get(b, c, mid + 1, high, idx * 2 + 1);
}
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
init(1, n, 1);
for (int i = 0; i < m + k; i++) {
int a;
int b;
long long c;
cin >> a >> b >> c;
if (a == 1) {
change(b, c, 1, n, 1, c - arr[b]);
arr[b] = c;
}
else if (a == 2) {
long long answer = get(b, c, 1, n, 1);
cout << answer << endl;
}
}
return 0;
}