https://www.acmicpc.net/problem/2206
문제
N×M의 행렬로 표현되는 맵이 있다. 맵에서 0은 이동할 수 있는 곳을 나타내고, 1은 이동할 수 없는 벽이 있는 곳을 나타낸다. 당신은 (1, 1)에서 (N, M)의 위치까지 이동하려 하는데, 이때 최단 경로로 이동하려 한다. 최단경로는 맵에서 가장 적은 개수의 칸을 지나는 경로를 말하는데, 이때 시작하는 칸과 끝나는 칸도 포함해서 센다.
만약에 이동하는 도중에 한 개의 벽을 부수고 이동하는 것이 좀 더 경로가 짧아진다면, 벽을 한 개 까지 부수고 이동하여도 된다.
한 칸에서 이동할 수 있는 칸은 상하좌우로 인접한 칸이다.
맵이 주어졌을 때, 최단 경로를 구해 내는 프로그램을 작성하시오.
입력
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 1,000)이 주어진다. 다음 N개의 줄에 M개의 숫자로 맵이 주어진다. (1, 1)과 (N, M)은 항상 0이라고 가정하자.
출력
첫째 줄에 최단 거리를 출력한다. 불가능할 때는 -1을 출력한다.
접근
일단 문제를 풀면서 DFS로 풀지 BFS로 풀지 고민했다. 살짝 생각해봤을 때는 둘 다 문제가 풀릴 것 같았다. 하지만 DFS는 보통 재귀 방식으로 해결하는데, N과 M의 범위를 보았을 때 재귀함수 호출을 1000번 이상 한다... 맵 내에 벽이 하나도 없다고 쳐도 답으로 나올 수 있는 값은 M + N - 1일텐데 DFS로 푼다는 것은 말이 안된다고 생각했다. 그래서 BFS로 풀게 되었다.
맨 처음에는 코드를 이렇게 짰었다.
#include <iostream>
#include <queue>
#include <string>
using namespace std;
struct Node {
int x; // x좌표
int y; // y좌표
int cnt; // 누적 거리
bool breakChance; // 벽을 부쉈는지 여부
Node(int xVal, int yVal, int cntVal, bool chance) {
x = xVal;
y = yVal;
cnt = cntVal;
breakChance = chance;
}
};
int map[1001][1001];
bool visited[1001][1001]{ false, };
// 상 하 좌 우
int dx[4]{ 0, 0, -1, 1 };
int dy[4]{ -1, 1, 0, 0 };
queue<Node> q;
int ans = -1;
int main() {
int n;
int m;
string str;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> str;
for (int j = 1; j <= m; j++) {
map[i][j] = str[j - 1] - '0';
}
}
q.push(Node(1, 1, 1, true));
visited[1][1] = true;
while (!q.empty()) {
Node node = q.front();
q.pop();
int curX = node.x;
int curY = node.y;
int cnt = node.cnt;
int chance = node.breakChance;
if (curX == m && curY == n) {
ans = node.cnt;
break;
}
else {
for (int i = 0; i < 4; i++) {
if (0 < curX + dx[i] && curX + dx[i] <= m && 0 < curY + dy[i] && curY + dy[i] <= n && !visited[curY + dy[i]][curX + dx[i]]) {
if (map[curY + dy[i]][curX + dx[i]] == 0) {
visited[curY + dy[i]][curX + dx[i]] = true;
q.push(Node(curX + dx[i], curY + dy[i], node.cnt + 1, node.breakChance));
}
else if (map[curY + dy[i]][curX + dx[i]] == 1 && node.breakChance) {
// 벽 부수고 지나가기
visited[curY + dy[i]][curX + dx[i]] = true;
q.push(Node(curX + dx[i], curY + dy[i], node.cnt + 1, false));
}
}
}
}
}
cout << ans << endl;
return 0;
}- 각 노드는 좌표, 누적 거리, 벽을 부쉈는지의 여부를 가지고 있다.
- 큐에서 노드를 하나씩 꺼내고 꺼낸 노드의 좌표를 기준으로 상하좌우를 조사한다.
(벽이 없고 방문하지 않은 좌표일 경우, 벽이 있고 부술 기회가 있는 경우 큐에 넣는다.)
접근 자체는 어느정도 했지만 한 가지 간과한 사실이 있었다.
중간에 한 번 벽을 부숴도, 부수지 않아도 목표 지점에 도달할 수 있는 경우도 생각해야 한다.
따라서, 벽을 한 번 부쉈을 경우, 부수지 않았을 경우에 대한 거리를 따로 저장하는 방법으로 바꿔서 코드를 아래와 같이 작성했다.
#include <iostream>
#include <queue>
#include <string>
using namespace std;
struct Node {
int x;
int y;
int breakChance;
Node(int xVal, int yVal, int chance) {
x = xVal;
y = yVal;
breakChance = chance;
}
};
int map[1001][1001];
int weight[1001][1001][2]{ 0, };
// 상 하 좌 우
int dx[4]{0, 0, -1, 1};
int dy[4]{-1, 1, 0, 0};
queue<Node> q;
int ans = -1;
int main() {
int n;
int m;
string str;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> str;
for (int j = 1; j <= m; j++) {
map[i][j] = str[j - 1] - '0';
}
}
q.push(Node(1, 1, 1));
weight[1][1][1] = 1;
while (!q.empty()) {
Node node = q.front();
q.pop();
int curX = node.x;
int curY = node.y;
int chance = node.breakChance;
if (curX == m && curY == n) {
ans = weight[curY][curX][chance];
break;
}
else {
for (int i = 0; i < 4; i++) {
if (0 < curX + dx[i] && curX + dx[i] <= m
&& 0 < curY + dy[i] && curY + dy[i] <= n ) {
if (map[curY + dy[i]][curX + dx[i]] == 0 && weight[curY + dy[i]][curX + dx[i]][chance] == 0) {
weight[curY + dy[i]][curX + dx[i]][chance] = weight[curY][curX][chance] + 1;
q.push(Node(curX + dx[i], curY + dy[i], node.breakChance));
}
else if (map[curY + dy[i]][curX + dx[i]] == 1 && chance == 1) {
// 벽 부수고 지나가기
weight[curY + dy[i]][curX + dx[i]][chance - 1] = weight[curY][curX][chance] + 1;
q.push(Node(curX + dx[i], curY + dy[i], chance - 1));
}
}
}
}
}
cout << ans << endl;
return 0;
}벽을 부쉈을 경우와 부수지 않았을 경우에 대한 거리를 각각 저장하기 위해
int weight[1001][1001][2]{ 0, };이렇게 3차원 배열을 선언했다.
(3차원 인덱스 값이 1이면 벽 부술 기회 o, 0이면 x)
또한, 방문 여부를 단순히 true, false로 구분했던 전 방법과 달리, 이번에는 거리 자체를 저장하여 0이 아닐 경우에는 방문했다는 것을 의미하는 쪽으로 작성했다.
중간에 한 번 벽을 부숴도, 부수지 않아도 목표 지점에 도달할 수 있는 경우도 생각해야 한다.
ex)
0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 0
여기서 빨간색으로 표시한 1을 부수면 거리 8로 도달할 수 있지만, 벽을 부수지 않는다면 거리 14가 소요된다. 한 눈에 이해하기 쉽게 코드에서 답을 도출하는 부분의 break;를 주석처리하고 각 경우에 대한 map을 출력해보았다.
인용절에서는 이미지 첨부가 뜻대로 안되길래 따로 빼게 되었다...
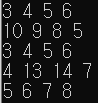
- 벽을 한 번 부순 경우
- 벽을 부수지 않은 경우
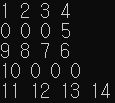
출력 시 정렬을 하지 않아 흐트러지긴 했지만 중간에 저장된 거리도 그렇고 도착 지점의 거리로 차이를 확인할 수 있다.